문제
N(2 ≤ N ≤ 100,000)개의 정점으로 이루어진 트리가 주어진다. 트리의 각 정점은 1번부터 N번까지 번호가 매겨져 있으며, 루트는 1번이다.
두 노드의 쌍 M(1 ≤ M ≤ 100,000)개가 주어졌을 때, 두 노드의 가장 가까운 공통 조상이 몇 번인지 출력한다.
입력
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정점 쌍이 주어진다.
해결
이 문제는 말 그대로 LCA 알고리즘을 사용하는 방법이다. LCA란 Lowest Common Ancestor의 약자로 트리 내의 두 정점에서 가장 가까운 공통 조상을 찾는 과정을 말한다.
예를 들어 이런 트리가 있다고 친다면...
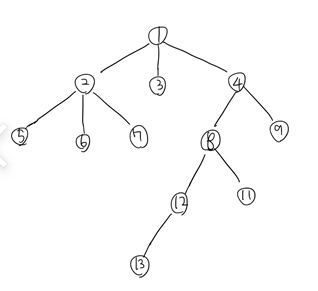
이렇게...
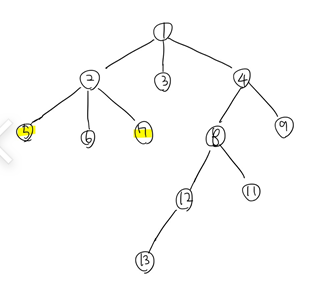
5와 7의 가장 가까운 공통 조상은 누구일까? 그들의 부모인 2라는 점을 단번에 알 수 있을 것이다!
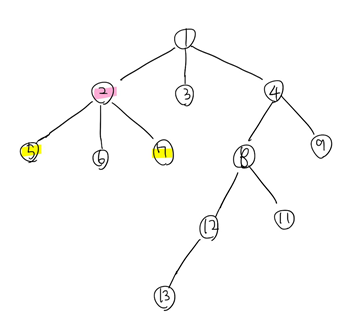
그렇다면 이번에는...
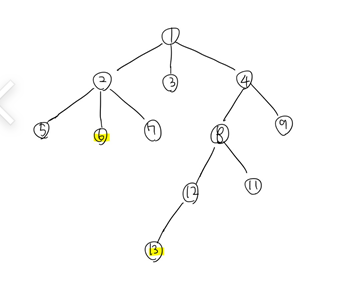
이렇게 극단적으로 6와 13의 가장 가까운 공통 조상은 누구일까?
아까와 같은 경우에는 두 노드의 레벨이 같아 동시에 루트 방향으로 거슬러 올라갔지만 이번에는 레벨이 다르므로 우선 아까처럼 출발점을 맞춰야 한다. 현재 6의 레벨은 3이고 13의 레벨은 5인 것을 보아 13의 레벨을 6에 맞춰야 한다는 사실을 알 수 있다. (레벨이 더 작은 쪽으로 출발점을 맞춰야 한다.)
레벨을 맞추기 위해 레벨을 맞추면 다음과 같다.
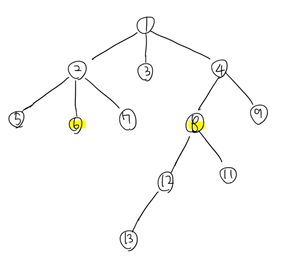
이제 출발점을 맞췄으니 루트 방향으로 동시에 거슬러 올라가다 보면
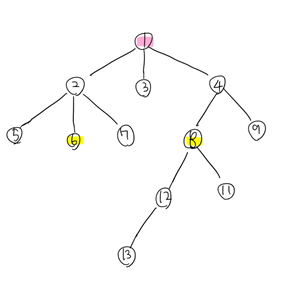
공통 조상으로 1을 만날 수 있게 된다.
처음에 본인은 이러한 과정을 떠올려 단순히 이렇게 코드를 작성했다.
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
int parent[50001];
int level[50001];
vector<int> arr[50001];
void dfs(int n, int lev);
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
parent[i] = -1;
level[i] = 0;
}
for (int i = 0; i < n - 1; i++) {
int n1;
int n2;
cin >> n1;
cin >> n2;
arr[n1].push_back(n2);
arr[n2].push_back(n1);
} // 그래프 생성
parent[1] = 1;
level[1] = 1;
dfs(parent[1], level[1]); // 트리 생성
int m;
cin >> m;
for (int i = 0; i < m; i++) {
int a;
int b;
cin >> a;
cin >> b;
if (level[a] > level[b]) {
while (level[a] != level[b]) {
a = parent[a];
}
}
else if (level[a] < level[b]) {
while (level[a] != level[b]) {
b = parent[b];
}
} // 두 노드의 출발점(레벨)을 맞추는 과정
while (a != b) {
a = parent[a];
b = parent[b];
} // 두 노드의 최단 공통 조상을 찾는 과정
cout << a << '\n';
}
return 0;
}
void dfs(int n, int lev) {
level[n] = lev;
for (int i = 0; i < arr[n].size(); i++) {
int val = arr[n].at(i);
if (parent[val] == -1) { // 부모가 없을 경우. 방문하지 않은 노드일 경우
parent[val] = n;
dfs(val, lev + 1);
}
}
}단순히 두 노드의 레벨을 조사한 후 출발점을 맞추고 공통 조상을 찾는 과정이다. 무작정 루트 방향으로 진행하는 방법으로 풀어나갔다. 이 경우에 최악의 경우 O(N)의 시간 복잡도가 요구되고 모든 과정을 처리하기 위해서는 O(MN)이라는 시간 복잡도가 요구된다.
https://www.acmicpc.net/problem/11437
백준에서 가장 기본 LCA를 해결하는 문제가 있는데 이 문제는 해결할 수 있다. 하지만, 오늘 풀이할 문제에서는 방금 그 방법으로는 시간 내에 해결할 수 없다. 똑같은 LCA인데... 더 빨리 해결할 수 있는 방법이 있을 것이다. 위의 방법은 그대로 지키되 거슬러 올라가는데 들이는 시간을 줄이고 싶다.
아까는 한 칸씩 루트 방향으로 진행했다면 이제는 2의 제곱만큼 거슬러 올라가는 방법을 사용할 것이다.
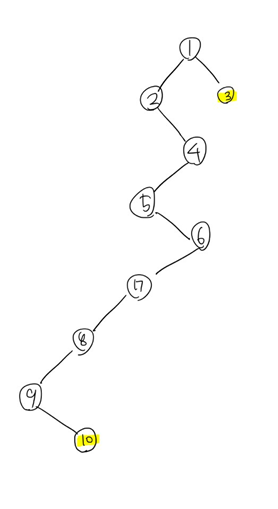
이런 그래프가 있다고 가정했을 때, 3과 10의 최단 공통 조상을 구해볼 예정이다. 아까와 같은 방법이라면 10에서 9 -> 8 -> 7 -> ... -> 2 라는 과정을 거쳐야 할 것이다. 하지만 좀 전에 말한 2의 배수만큼 건너뛰는 방법을 생각해보면...
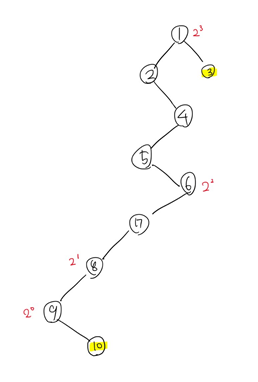
10의 관점에서 2^0, 2^1, 2^2, 2^3을 썼는데 이는 10으로부터 루트 방향으로 떨어져 있는 거리이다. 우리는 최대한 3과 가깝게, 하지만 3보다는 레벨이 낮아지지 않을 만큼 나아가야 한다. 따라서 지금 상황에서는 10과 2^2만큼 덜어져 있는 6으로 자리를 옮겨야 한다.
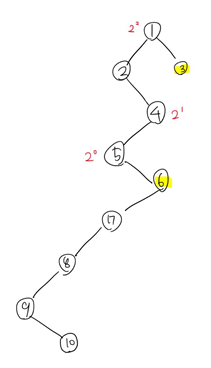
이렇게! 옮긴 후 6의 관점에서 루트 방향으로의 거리를 따져봤다. 아까와 같이 3과 최대한 가깝게, 3보다는 레벨이 낮아지지 않게... 이 조건을 생각해서 본다면 2^1만큼 떨어진 4로 자리를 옮겨야 한다는 것을 알 수 있다.
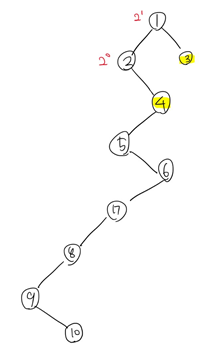
4로 옮긴 후 아까와 같은 과정을 거치면...
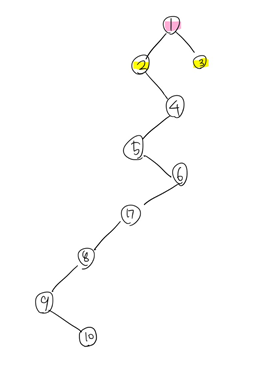
이런 결과가 나오고 이후 최단 공통 조상은 1이라는 사실 또한 구할 수 있다.
이제 지금까지의 과정을 코드를 통해 살펴볼 예정이다.
#include <iostream>
#include <vector>
using namespace std;
vector<int> arr[100001]; // 그래프
int dp[20][100001]; // 본인과 특정 노드와의 거리를 위한 dp배열
int level[100001]; // 노드의 레벨(깊이)
void dfs(int n, int lev);
int main() {
int n;
scanf_s("%d", &n);
for (int i = 0; i < n - 1; i++) {
int n1;
int n2;
scanf_s("%d %d", &n1, &n2);
arr[n1].push_back(n2);
arr[n2].push_back(n1);
}
...이 부분에는 코드에서 사용될 요소들과 단순히 그래프를 입력받는 부분이다.
이 과정을 마친 후...
void dfs(int n, int parent) {
level[n] = level[parent] + 1; // 레벨
dp[0][n] = parent; // n의 부모
int maxLevel = (int)floor(log2(100001));
for (int i = 1; i < maxLevel; i++) {
dp[i][n] = dp[i - 1][dp[i - 1][n]];
}
for (int i = 0; i < arr[n].size(); i++) {
int tmp = arr[n].at(i);
if (tmp != parent) {
dfs(tmp, n);
} // 중복 방지
}
}지금까지 봐왔던 트리를 구성하기 위해(정확히는 본인과 2의 제곱수만큼 떨어진 노드가 무엇이 있는가에 대한 관계를 구성하기 위해) dp와 dfs를 이용한다.
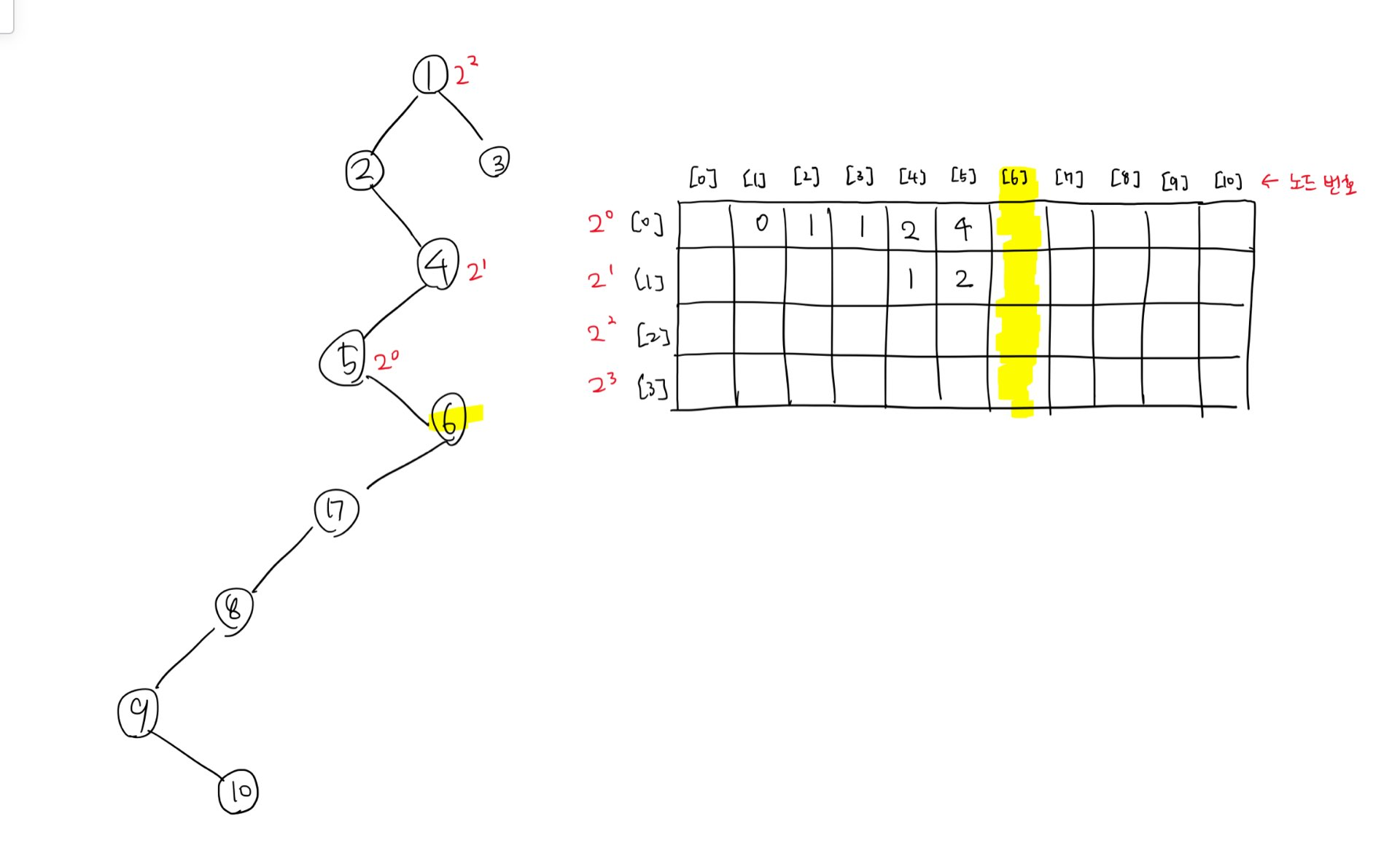
이미지 내 오른쪽의 표는 dp 표다. 행번호는 2^n의 n을, 열번호는 노드번호를 의미한다. 이 안에는 본인 노드와 루트 방향으로 2^n만큼 떨어진 곳에 몇 번 노드가 있을지를 담을 것이다. 이제 6번 노드에 대해서 과정을 적어볼 예정이다.
(중간 과정을 생략하고 미리 적어놓았다. 앞에 있는 값들도 이제 알아볼 방법과 같은 방법으로 채워넣은 것이다.)
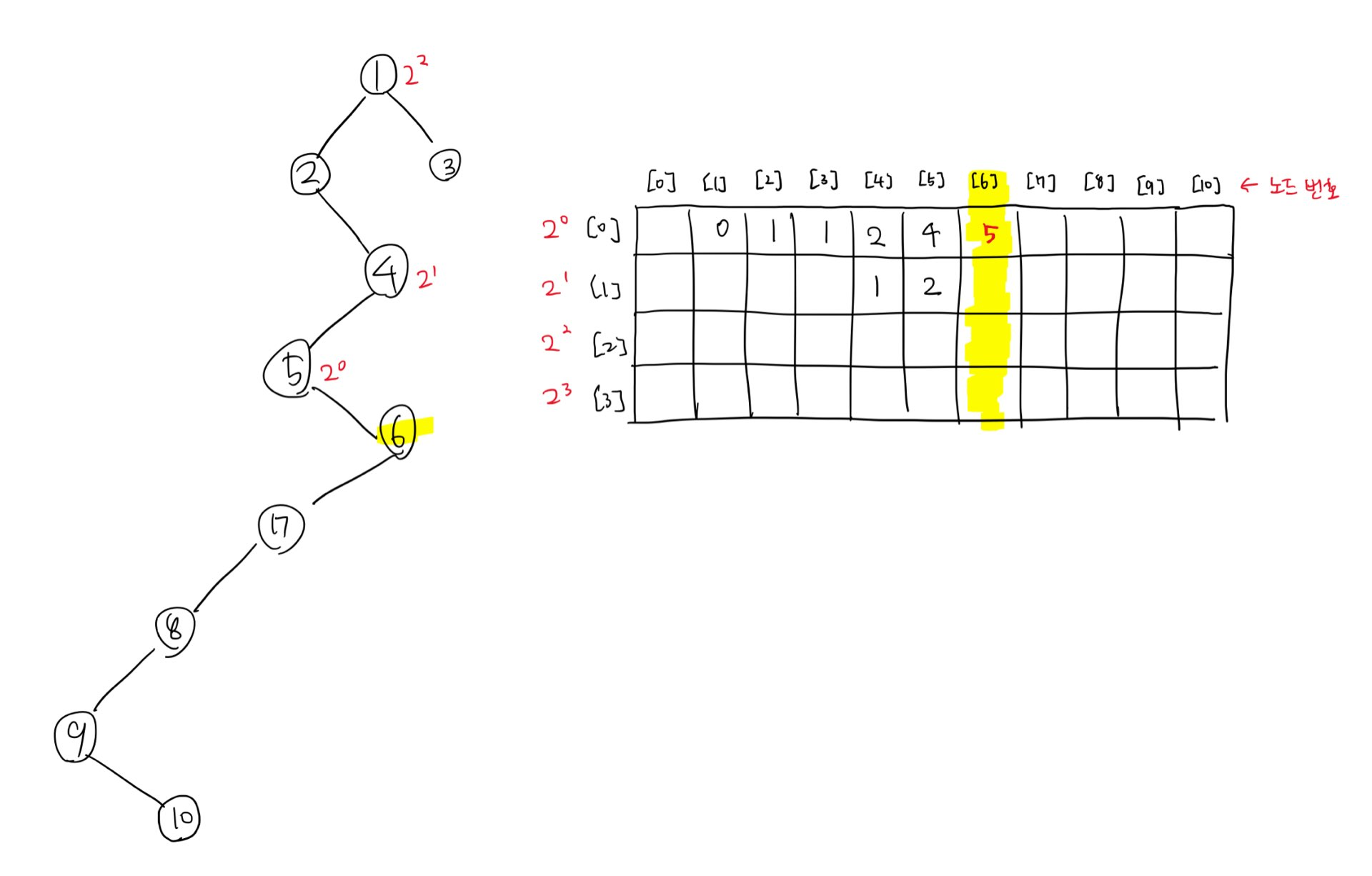
우선 dp[0][6] 위치에 5를 적어놨는데 이는 6과 루트 방향으로 2^0만큼 떨어진 곳에 5가 있다는 것을 적어준 것이다.
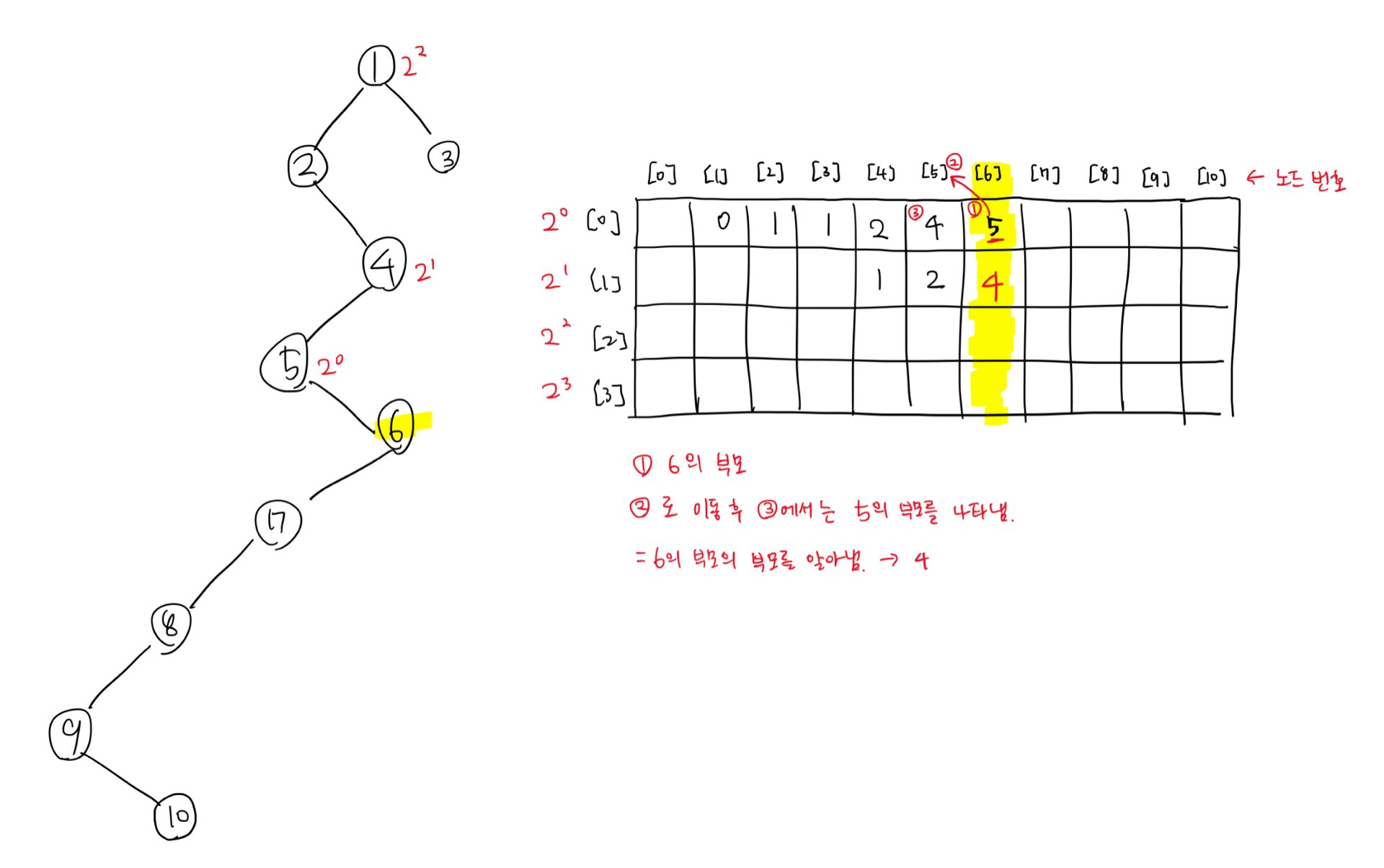
이제 6과 루트 방향으로 2^1만큼 떨어진 노드가 누구인지 알아내야 한다.
- 본인(6)과 2^(n - 1)만큼(지금 상황에서는 1) 떨어진 값을 알아낸다.
- 해당 값에 대한 인덱스로 이동한다.
- 그 인덱스(노드)에서 2^(n - 1)만큼 떨어진 노드를 조사한다.
이 과정을 거치면 현재 6으로부터 2^0칸 떨어진 노드인 5 -> 5로부터 2^0칸 떨어진 노드는 4라는 사실을 알게 된다.
(=6으로부터 2^1칸 떨어진 노드의 값은 4다.)
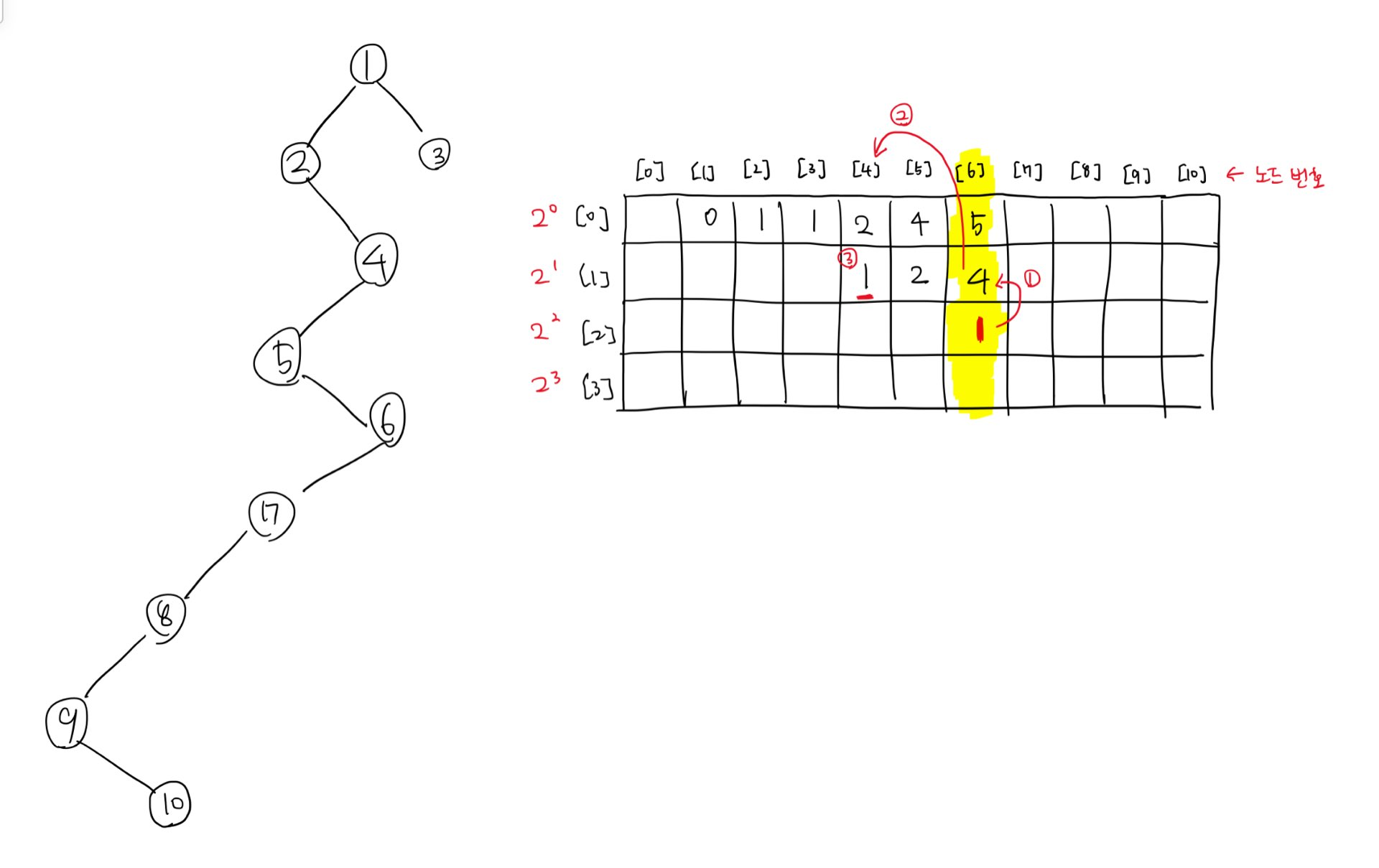
방금 말한 방법을 적용해서 6에서 루트 방향으로 2^2만큼 떨어진 노드의 값을 적용한다.
1. 본인(6)과 2^(n - 1)만큼(지금 상황에서는 2) 떨어진 값을 알아낸다.
2. 해당 값에 대한 인덱스로 이동한다.
3. 그 인덱스(노드)에서 2^(n - 1)만큼 떨어진 노드를 조사한다.
즉, 6으로부터 2^1칸 떨어진 노드의 값 4 -> 4로부터 2^1칸 떨어진 노드의 값은 1이므로 6으로부터 2^2만큼 떨어진 노드의 값을 구할 수 있게 된다.
...이러한 과정을 모든 노드에 대해서 반복한다. 그러면
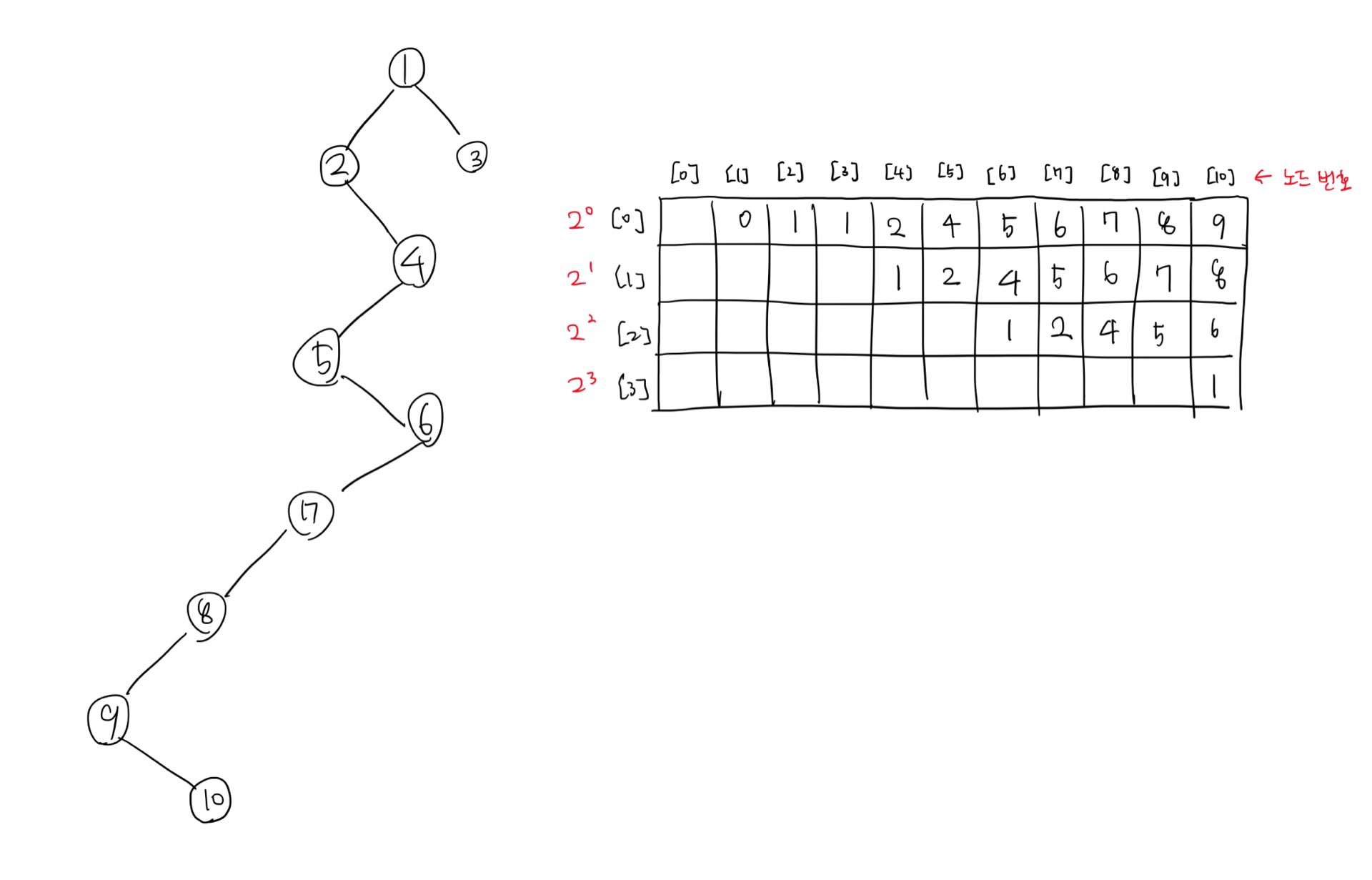
이렇게 채워진다.
이제 이렇게 채운 dp 표를 가지고 문제를 해결할 것이다.
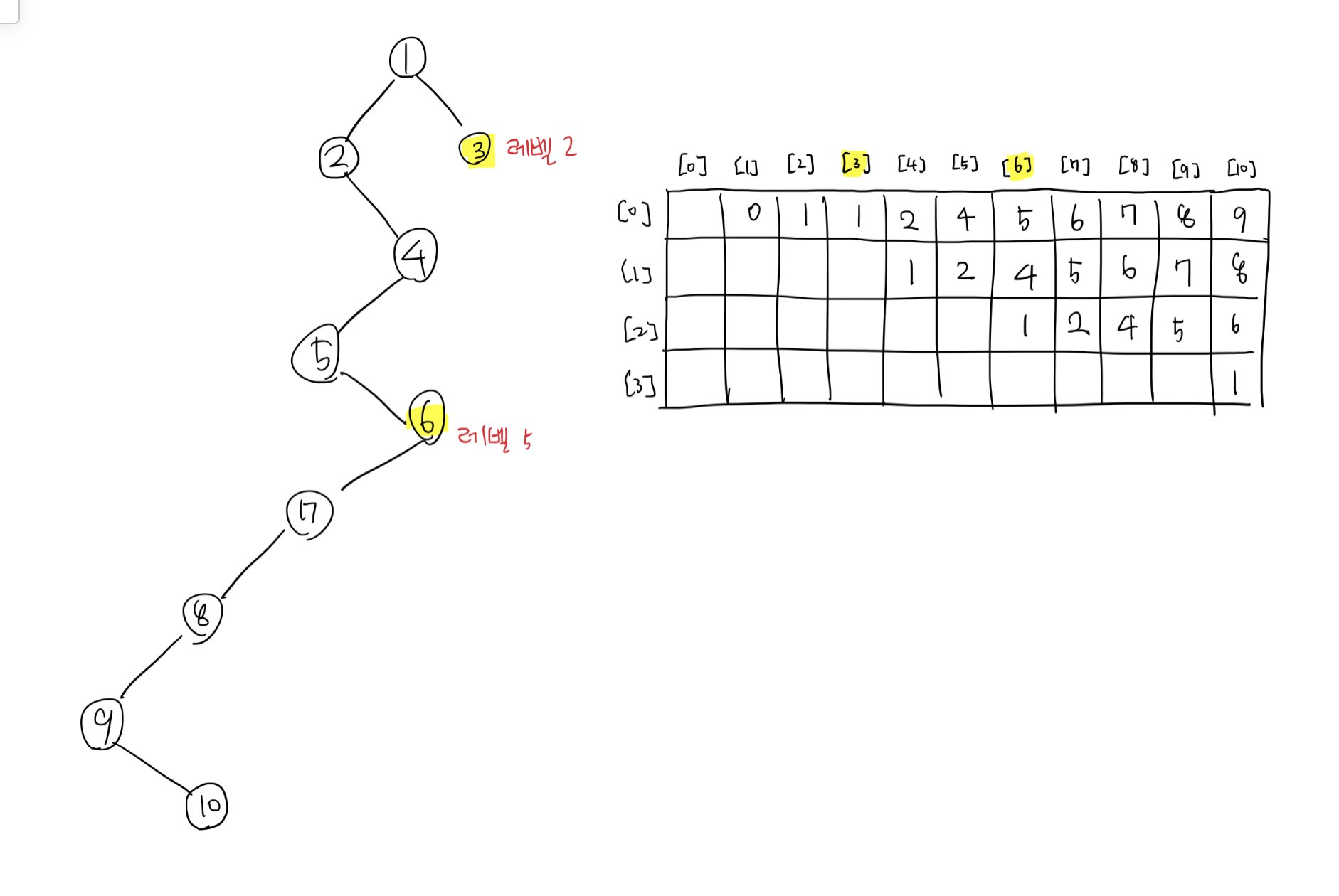
표시한 노드 6과 3의 최단 공통 조상을 구하기 위해 우선 둘의 레벨을 맞춘다고 가정해보자.
int a;
int b;
scanf_s("%d %d", &a, &b);
if (level[a] != level[b]) {
if (level[a] > level[b]) {
swap(a, b); // b의 레벨을 더 높은 레벨로 두기 위한 과정
}
for (int j = 20 - 1; j >= 0; j--) {
if (level[a] <= level[dp[j][b]]) {
b = dp[j][b];
}
}
}코드는 다음과 같다. for문이 두 노드의 레벨을 맞추는 과정이다.
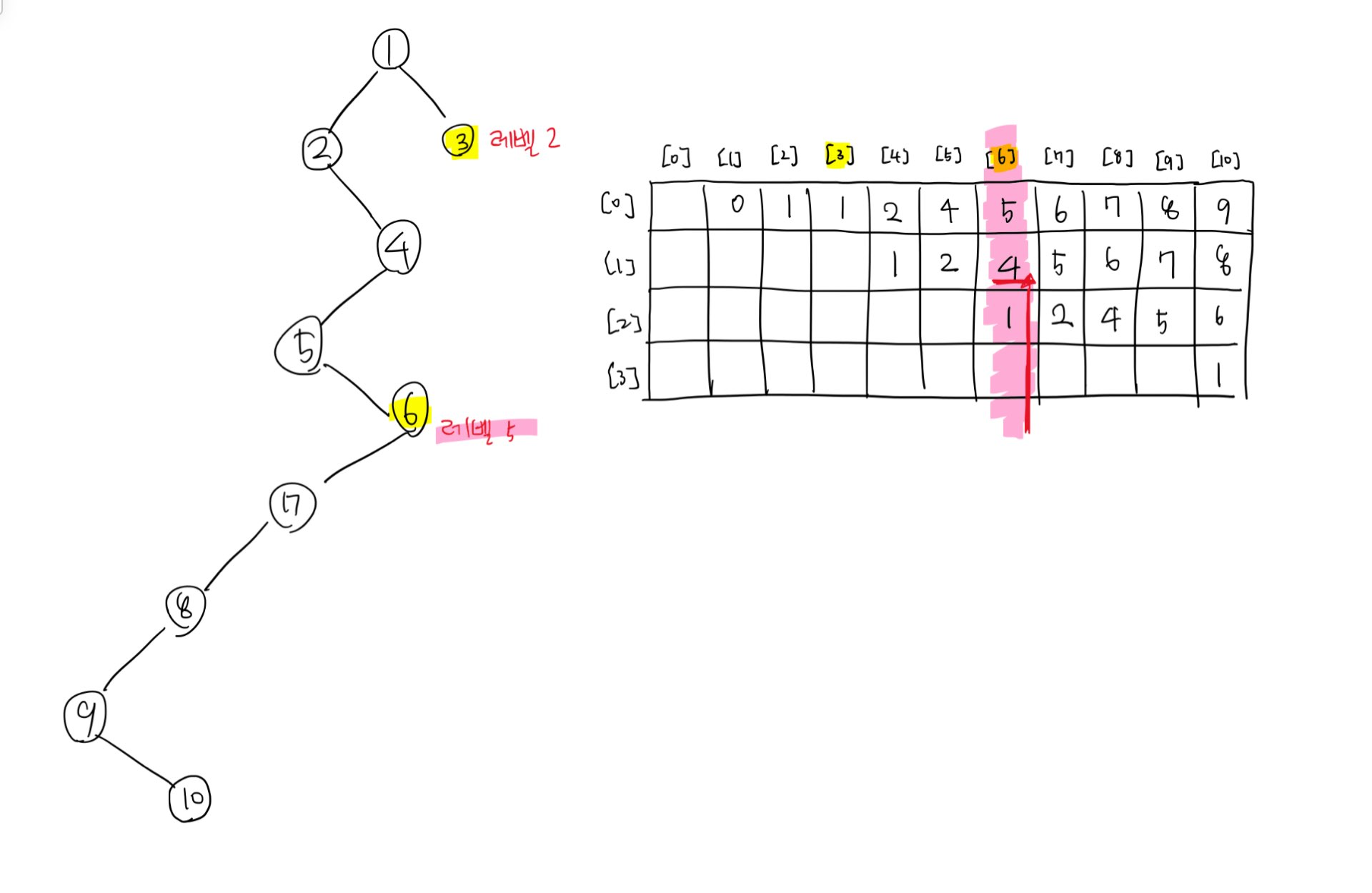
현재 6의 레벨이 3보다 높으니 이에 대한 레벨을 낮춰야 한다. 따라서 for문으로 루트에서 가장 먼 방향에서 루트 방향으로 해당 인덱스 내의 값의 레벨이 낮아지는 첫 지점을 찾는다. 행 번호가 커질수록 현재 기준이 되는 노드로부터 거리가 멀어진다는 것을 의미한다. 그래서 밑에서부터 조사한다는 것은 최대한 상대 노드보다 레벨은 같거나 높도록 하되, 본인으로부터는 떨어뜨리게 된다.
이제 b = dp[j][b];에서 걸리게 되고 노드 4를 기준으로 다시 조사한다. 기준 노드로부터의 거리를 나타내기 위한 2^n에서 n은(여기서는 j) 건드리지 않고 그대로 진행한다.
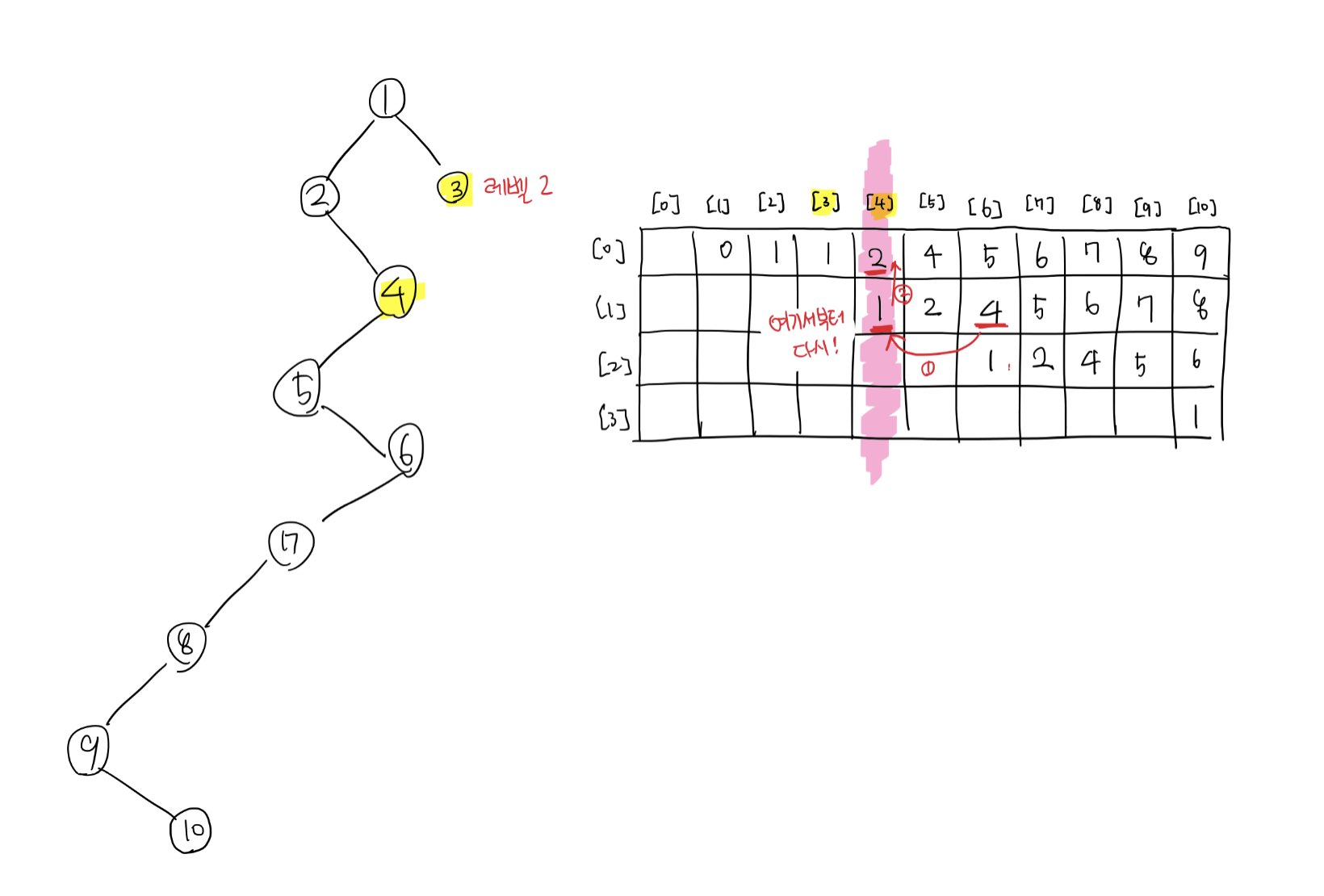
이제 4를 기준으로, 시작점은 좀 전에 멈췄던 부분부터 다시 윗방향으로 조사한다. 아까와 같은 원리로 2라는 값(4로부터 2^0만큼 떨어진 노드 값)에서 걸린다는 사실을 알게 된다. 이제 노드 2를 기준으로 다시 조사한다.
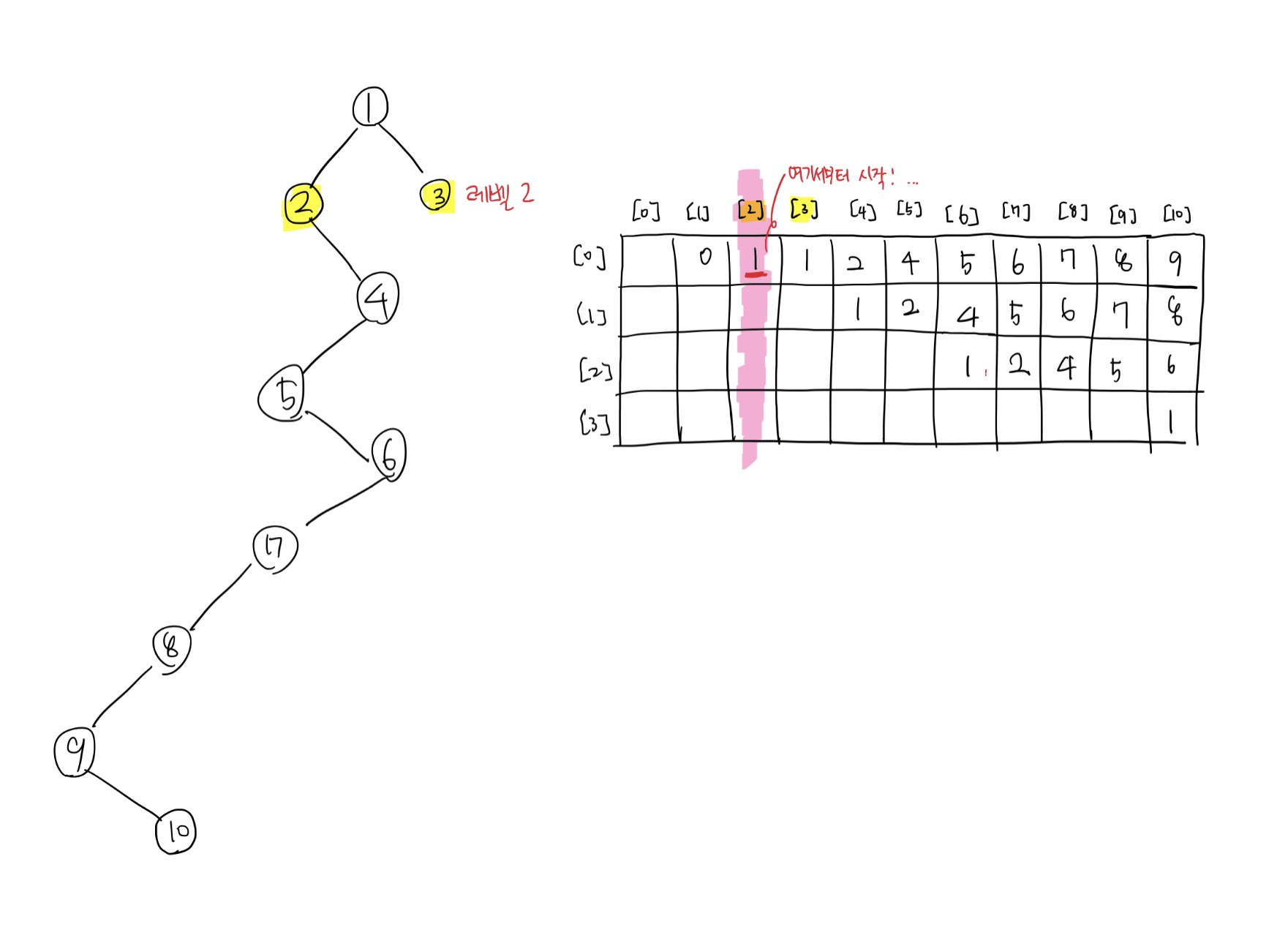
다시 노드 2를 기준으로 그 위치부터 윗방향으로 조사한다. 마침 조사가 끝났다. 2와 3의 레벨이 2로 같다는 것을 알 수 있다.
int ans = a; // 답
if (a != b) {
for (int j = 20 - 1; j >= 0; j--) {
if (dp[j][b] != dp[j][a]) {
a = dp[j][a];
b = dp[j][b];
}
ans = dp[j][a];
}
}
printf_s("%d\n", ans);이제 레벨을 맞췄으니 두 노드를 기준으로 동시에 루트를 향해 건너 뛰는 작업만 진행해주면 된다. 같은 레벨 상의 두 노드의 값이 다를 때 진행해주면 되며 원리는 레벨을 맞추는 과정과 비슷하다.
(레벨을 맞추는 과정에서는 한 노드에 대해서만 진행해줬다면 이번에는 두 노드 동시에 이 과정을 거치면 된다.)
전체 코드는 다음과 같다.
#include <iostream>
#include <vector>
#include <stdio.h>
#include <cmath>
using namespace std;
vector<int> arr[100001];
int dp[20][100001];
int level[100001];
void dfs(int n, int lev);
int main() {
int n;
scanf("%d", &n);
for (int i = 0; i < n - 1; i++) {
int n1;
int n2;
scanf("%d %d", &n1, &n2);
arr[n1].push_back(n2);
arr[n2].push_back(n1);
}
dfs(1, 0);
level[0] = -1;
int m;
scanf("%d", &m);
for (int i = 0; i < m; i++) {
int a;
int b;
scanf("%d %d", &a, &b);
if (level[a] != level[b]) {
if (level[a] > level[b]) {
swap(a, b);
}
for (int j = 20 - 1; j >= 0; j--) {
if (level[a] <= level[dp[j][b]]) {
b = dp[j][b];
}
}
} // 두 노드의 레벨 맞추기
int ans = a;
if (a != b) {
for (int j = 20 - 1; j >= 0; j--) {
if (dp[j][b] != dp[j][a]) {
a = dp[j][a];
b = dp[j][b];
}
ans = dp[j][a];
}
} // 최소 공통 조상 찾기
printf("%d\n", ans);
}
return 0;
}
void dfs(int n, int parent) {
level[n] = level[parent] + 1;
dp[0][n] = parent;
for (int i = 1; i < 20; i++) {
dp[i][n] = dp[i - 1][dp[i - 1][n]];
}
for (int i = 0; i < arr[n].size(); i++) {
int tmp = arr[n].at(i);
if (tmp != parent) {
dfs(tmp, n);
}
}
} // 트리 생성용 dfs+ 오랜만에 다시 풀어봤는데 놓치는 부분이 몇 군데 있었다.
1. 인덱스 혼동
2. dfs 초기값
3. 같은 레벨에 있는 두 값을 찾았을 때
1. 인덱스
2차원 dp 배열 (행 : 2^n의 n, 열 : 노드번호)은 dfs 탐색하면서 한 노드를 기준으로 세로 방향으로 채워나간다. 따라서 for문에서 사용하는 배열을 행 번호로 사용해야 한다.
2. dfs 초기값
dfs의 인자로 현재 노드 번호와 부모 노드 번호를 받는다. 이때, 루트노드인 1번 노드의 부모는 0이다. 따라서 dfs(1, 0)과 같이 호출해야 한다.
(본인은 오랜만에 풀 때 루트의 부모는 자기 자신이라고 착각하고 dfs(1, 1)과 같이 넣었다...)
3. 같은 레벨에 있는 두 값을 찾았을 때int ans = a; if (a != b) { for (int j = 20 - 1; j >= 0; j--) { if (dp[j][b] != dp[j][a]) { a = dp[j][a]; b = dp[j][b]; } ans = dp[j][a]; } } // 최소 공통 조상 찾기코드상 이 부분이고 여기서 a와 b는 레벨이 같은 두 노드이다. 두 노드는 레벨은 확실히 같고, 값은 같을 수도 있고 다를 수도 있다.
값은 같을 수도 있고 다를 수도 있다!
그래서 a != b라는 조건이 반드시 필요해진다.
이 조건을 걸어주지 않으면 두 노드의 값이 같든 다르든 가장 가까운 공통부모를 찾는 작업을 진행할거고, 만약 a와 b가 같았더라면 처음에 입력했던 a와 b의 가장 가까운 공통 조상의 가장 가까운 공통 조상을 찾게 되는 것이다...
