문제
방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 10 이하의 자연수이다.
입력
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K≤V)가 주어진다. 셋째 줄부터 E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수 (u, v, w)가 순서대로 주어진다. 이는 u에서 v로 가는 가중치 w인 간선이 존재한다는 뜻이다. u와 v는 서로 다르며 w는 10 이하의 자연수이다. 서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수도 있음에 유의한다.
출력
첫째 줄부터 V개의 줄에 걸쳐, i번째 줄에 i번 정점으로의 최단 경로의 경로값을 출력한다. 시작점 자신은 0으로 출력하고, 경로가 존재하지 않는 경우에는 INF를 출력하면 된다.
문제 해결
일단 문제에서 방향그래프라고 제시되어 있고 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램이라고 하였으니 다익스트라 알고리즘을 사용해야 한다는 것을 알 수 있다.
본인이 적어본 다익스트라 알고리즘이란...
1. 시작점으로부터 나가는 화살표와 연결된 정점들을 찾은 후 가중치를 해당 정점의 값으로 저장한다.
2. 배열에 저장된 가중치 중 가장 작은 가중치를 지닌 정점을 찾는다. 이 시점에서 정점 하나를 방문했다고 볼 수 있다. (단, 1의 과정에 해당되는 정점이어야 한다.)
3. 찾은(방문한) 정점으로부터 나가는 화살표와 연결된 정점들을 찾은 후 각각 찾은 정점까지의 가중치와 나가는 화살표와 연결된 정점까지의 가중치를 더한 값을 구한다.
- 값이 저장되어있지 않은 경우
위에서 구한 값을 배열의 해당 인덱스(화살표와 연결된 정점)의 값으로 저장한다. - 값이 저장되어 있는 경우
배열의 해당 인덱스의 값(가중치)과 위에서 구한 값을 비교한 후 구한 값이 더 작을 경우 해당 인덱스의 값을 갱신해준다. 이 말은 즉, 화살표와 연결된 정점을 가기 위해서는 본인을 거쳐야 더 작은 비용으로 도착할 수 있다는 의미가 된다.
- 가중치가 확정된 정점 외 나머지 정점들 중 최소 가중치를 지닌 정점을 찾는다.
- 모든 정점에 대한 가중치가 정해질 때까지 3과 4의 과정을 반복한다.
여기서 본인은 방향그래프를 구현하기 위해 '자료형이 벡터인 배열'을 생성하였으며 다익스트라 알고리즘을 구현하기 위해 '우선순위 큐'를 사용하였다.
본인은 자바로 그래프를 구현할 때 '자료형이 리스트인 배열'을 자주 사용하였다. 왼쪽과 같은 그래프를 오른쪽과 같이...!
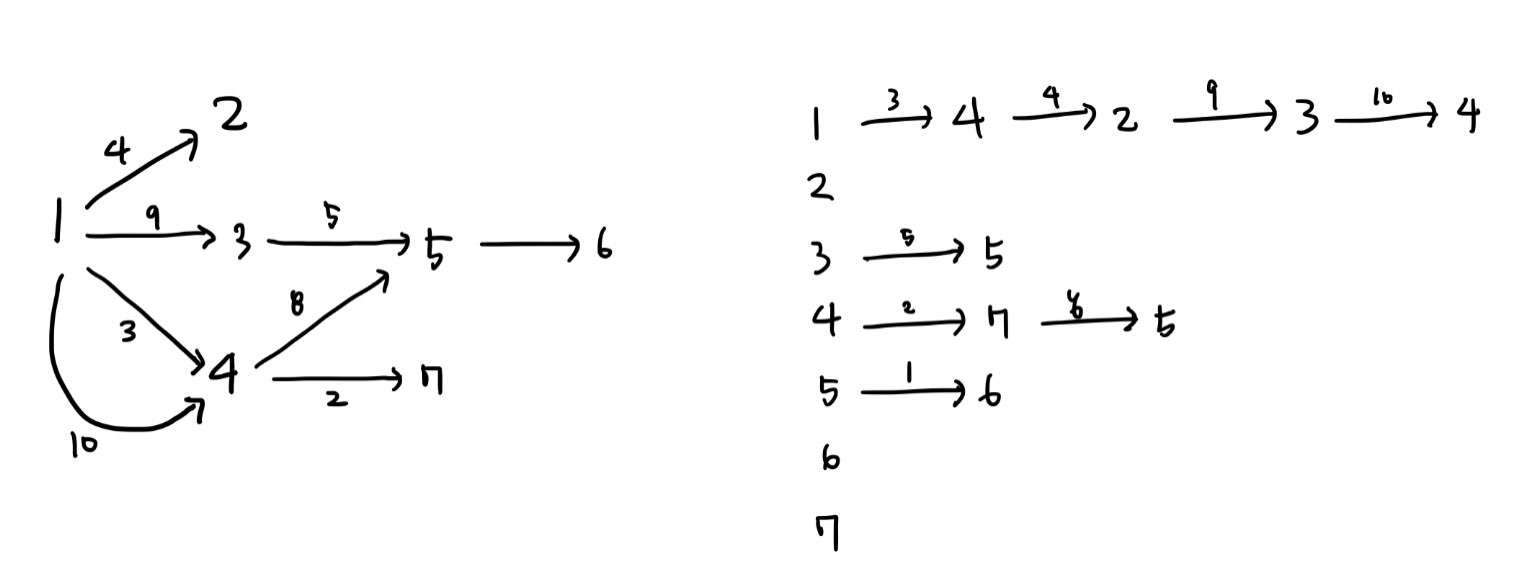
알고리즘 수업 때 C++에서는 벡터를 제공해준다는 이야기를 듣고 찾아서 쓰게 되었다.
#include <vector>
struct Node {
int key;
int value;
Node(int k, int v) : key(k), value(v) {
}
};
int main(){
vector<Node> graph[20001];
return 0;
}그래프상의 정점과 가중치를 담을 구조체 Node를 만들어주고 그 Node형 벡터가 자료형인 배열을 만들어주었다. (V가 최대 20000이라서 크기는 20001로 두었다.)
이제 시작점에서 특정 점까지의 최소 가중치를 구하기 위한 우선순위 큐가 필요하다.
#include <queue>
struct Sort {
bool operator()(Node a, Node b) {
return a.value > b.value;
}
};
int main(){
priority_queue<Node, vector<Node>, Sort> pq; // 우선순위 큐
int weight[20001]; // 정답 배열
return 0;
}
또한, 시작점으로부터 본인 정점까지의 최소 가중치를 저장할 배열 weight도 생성해줬다.
우선순위큐에는 정점과 최소가중치를 담고있는 Node를 넣어주기로 하였으며 정렬 기준은 가중치로 두고 가중치가 작은 노드를 앞쪽으로 뺐다. 그래야 방문하지 않은 정점 중 최소 가중치를 가진 정점을 찾을 수 있을 것이라고 생각했기 때문이다.
weight[startNum] = 0; // 첫 번째 정점 가중치 0
pq.push(Node(startNum, 0));
while (!pq.empty()) {
Node n = pq.top();
pq.pop();
int key = n.key;
int value = n.value;
for (int i = 0; i < graph[key].size(); i++) {
Node tempNode = graph[key].at(i);
int nextVal = value + tempNode.value;
if (weight[tempNode.key] == -1 || (nextVal < weight[tempNode.key])) { // 방문하지 않은 점이나 갱신될 점의 가중치가 더 작은 경우
weight[tempNode.key] = nextVal;
tempNode.value = nextVal; // 가중치를 누적시킨 후 큐에 삽입
pq.push(tempNode);
}
}
}우선순위 큐에서 노드를 뺐을 때 해당 정점을 방문하는 것이라고 여기고 그 정점으로부터 나아가는 방향의 정점들을 조사하였다.
1) 나아가는 방향의 정점을 한 번도 방문하지 않았을 때
2) weight 배열의 해당 인덱스의 값(현재까지의 최소 가중치)과 본인까지의 가중치에 본인과 새로 나아갈 정점 간의 가중치를 더한 값을 비교하여 후자가 더 작을 경우
1)과 2) 중 하나라도 해당된다면 갱신하는 과정을 거쳤으며 갱신하게 된다면 정점과 최소가중치를 담은 Node를 우선순위 큐에 넣었다. 이 때, 가중치에는 단순히 두 정점 간의 가중치가 아닌 본인까지의 가중치에 본인과 새로 나아갈 정점 간의 가중치를 더한 값을 두어야 한다.
왜...?
우선순위 큐에서 노드를 빼는 것
= 해당 정점을 방문하는 것
= 해당 정점의 최소 가중치는 결정된 것
따라서 적어도 우선순위 큐에 있는 가중치는 곧 본인의 가중치가 된다는 뜻이며 연결된 정점의 최소 가중치를 결정하는데도 영향을 주기 때문이다.
1)과 2)에 해당되지 않는다면? 굳이 우선순위 큐에 넣을 필요 없다. 방문한 전적이 있고 본인을 거쳐가지 않으면 더 빠른 길로 갈 수 있을텐데 더이상 조사할 필요가 없어진다.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
struct Node {
int key;
int value;
Node(int k, int v) : key(k), value(v) {
}
};
struct Sort {
bool operator()(Node a, Node b) {
return a.value > b.value;
}
};
int main() {
priority_queue<Node, vector<Node>, Sort> pq;
vector<Node> graph[20001];
int weight[20001];
int v;
int e;
int startNum;
cin >> v;
cin >> e;
cin >> startNum;
for (int i = 1; i <= v; i++) {
weight[i] = -1;
}
for (int i = 0; i < e; i++) {
int start;
int end;
int val;
cin >> start >> end >> val;
graph[start].push_back(Node(end, val));
}
weight[startNum] = 0; // 첫 번째 정점 가중치 0
pq.push(Node(startNum, 0));
while (!pq.empty()) {
Node n = pq.top();
pq.pop();
int key = n.key;
int value = n.value;
for (int i = 0; i < graph[key].size(); i++) {
Node tempNode = graph[key].at(i);
int nextVal = value + tempNode.value;
if (weight[tempNode.key] == -1 || (nextVal < weight[tempNode.key])) { // 방문하지 않은 점이나 갱신될 점의 가중치가 더 작은 경우
weight[tempNode.key] = nextVal;
tempNode.value = nextVal; // 가중치를 누적시킨 후 큐에 삽입
pq.push(tempNode);
}
}
}
for (int i = 1; i <= v; i++) {
if (weight[i] == -1) {
cout << "INF" << '\n';
}
else {
cout << weight[i] << '\n';
}
}
return 0;
}전체 코드는 이렇다.
잠깐만... 우선순위 큐에서 노드를 빼는 순간 무조건 정점을 방문하는 것일까...? 모든 정점을 방문하기 전까지는 그렇지만 그 뒤부터 빼는 노드에 대해서는 그렇지 않다. 노드가 많으면 많을수록 한 정점에 대해서 가중치가 계속 갱신될 수도 있기 때문에 우선순위 큐에 노드가 들어가는 횟수는 정점의 수보다 거의 많을 것이라고 본다. 코드에서는 그런 상황에 대해 딱히 조치를 취하지 않았지만 우선순위 큐로부터 정점의 수만큼 노드를 빼는 작업을 했으면 빠져나오는 등의 조치를 취해줘도 괜찮을 것 같다는 생각이다.
(크게 차이가 있을까 싶긴 하지만...)
