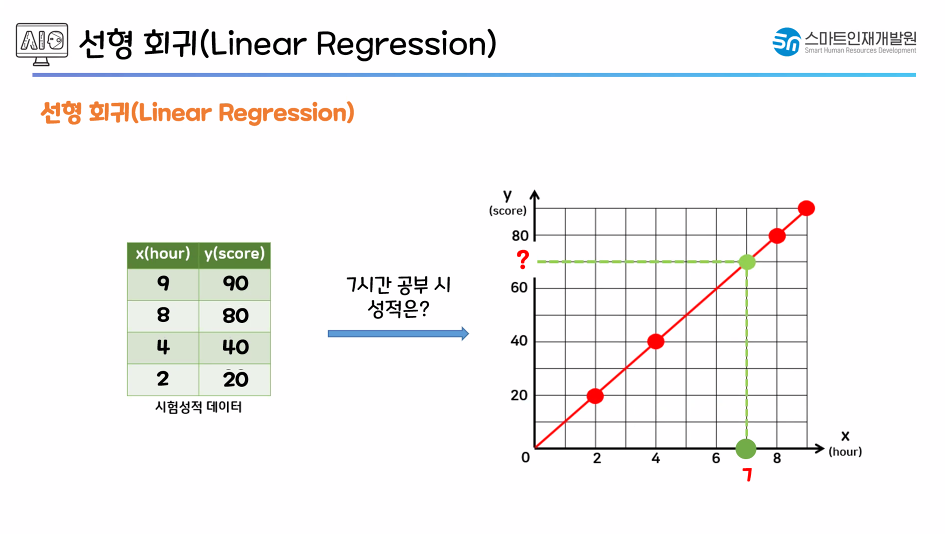
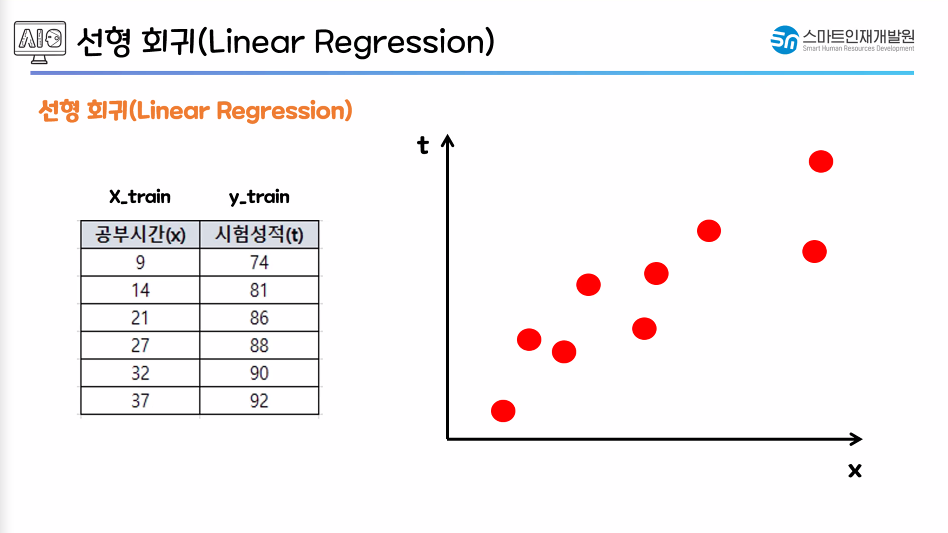
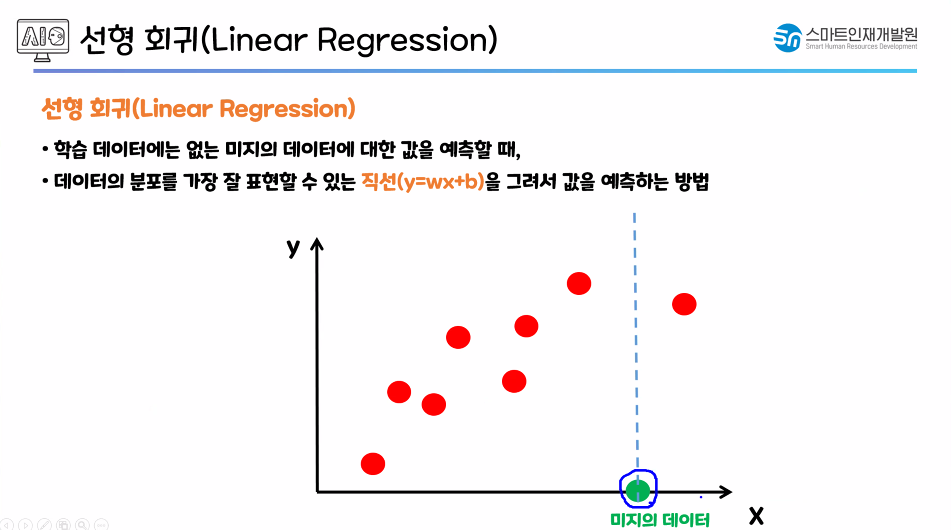
x : 독립변수 / 특성값(데이터의 특성) / 컬럼
y : 종속변수 / 예측값 / 예측한 정답
w : 가중치 / 특성의 정답 관여율(최적의 값을 과정을 통해 알아서 찾음)
b : 절편 / 편향 → y = wx라는 회귀 직선을 y축 방향으로 얼마나 수직 평행 이동 시키는지?
w의 중요도에 따라 예측율에 관여 10,20% ...
특성(x)의 개수 → 수식에서 x의 개수, x의 개수만큼 w(가중치)의 개수
(MSE가 중요하다.)
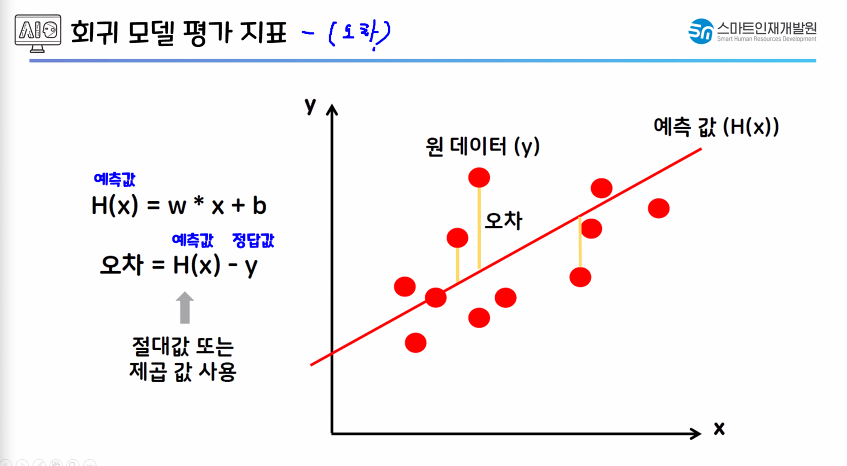오차 : 예측값 - 실제값(차이값)
오차가 작아야함.
오차값을 절대값, 제곱값을 사용하지 않으면 음수,양수값을 평균냈을 때 원하는 오차값과 의미가 다른 값이 나올 수 있음.
- 제곱값을 더 많이 사용하는 이유
- 미분하였을 때 이차항으로 만드는게 좋기때문
- 모델이 오차값이 클수록 더 값을 잘 찾으려고함.
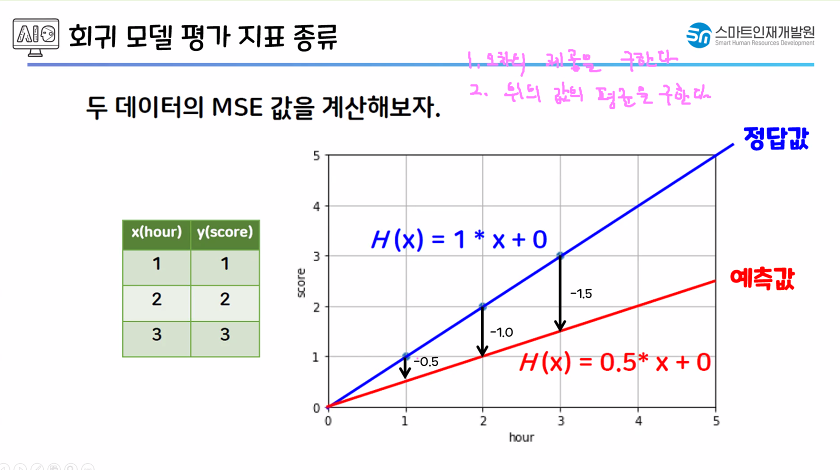
1. 오차의 제곱을 구한다.
2. 위의 값의 평균을 구한다.
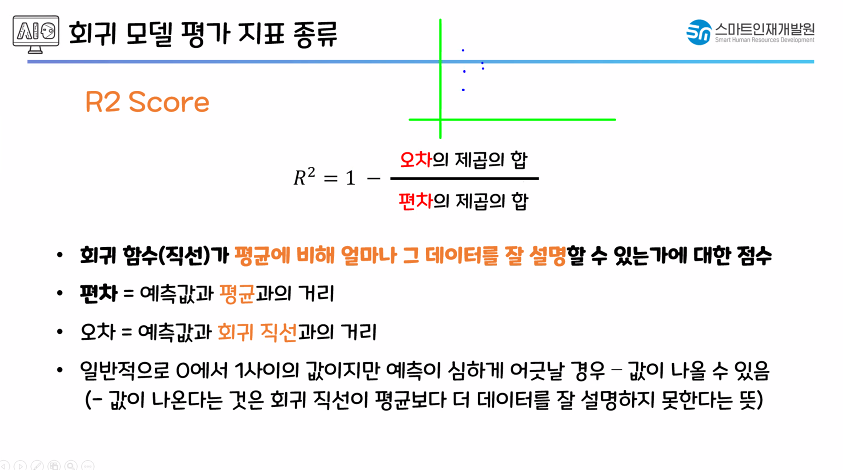
R2 Score : 0~1(1 → 성능 good, 0 → 성능 bad), -1(값이 아예 틀어졌다)
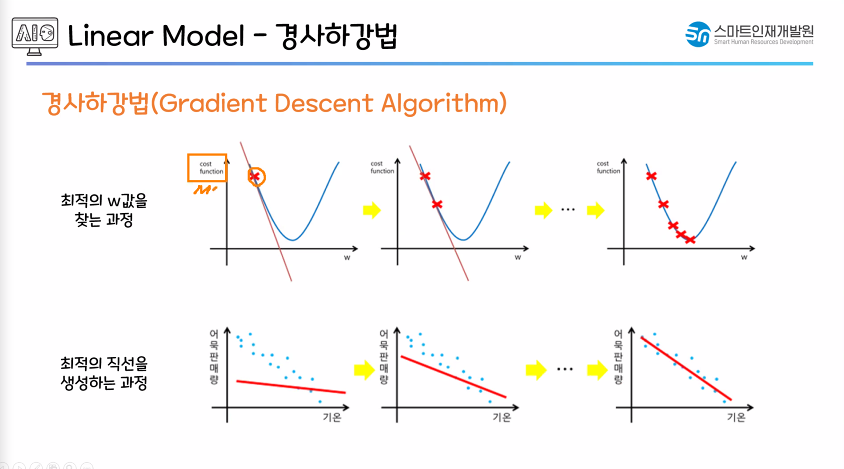
MSE가 최소가 되는 최적의 w,b값 구하기
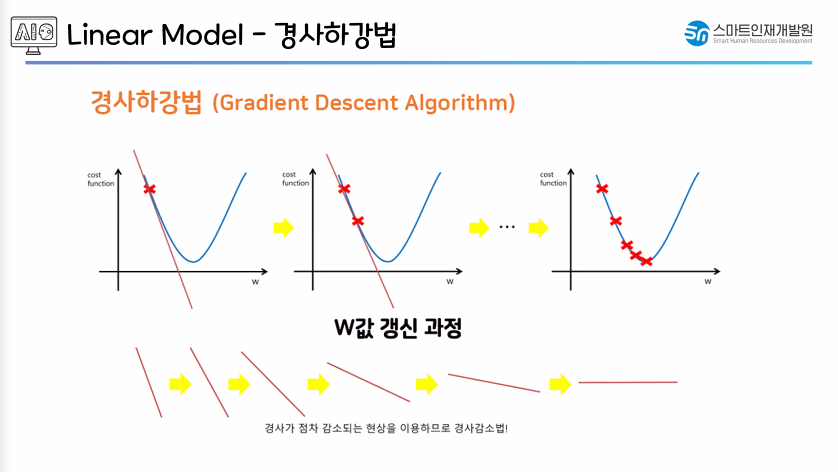
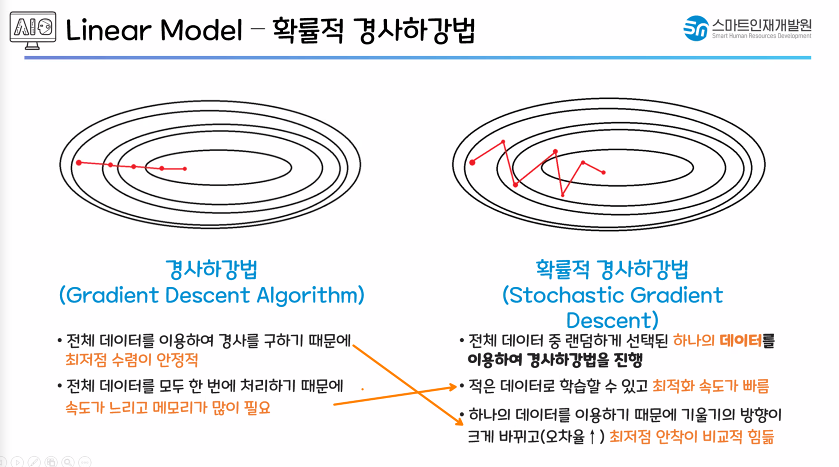
- 경사하강법 : 최적의 가중치, 편향을 구하기 위한 방법론 중 하나(연산, 경사하강법)
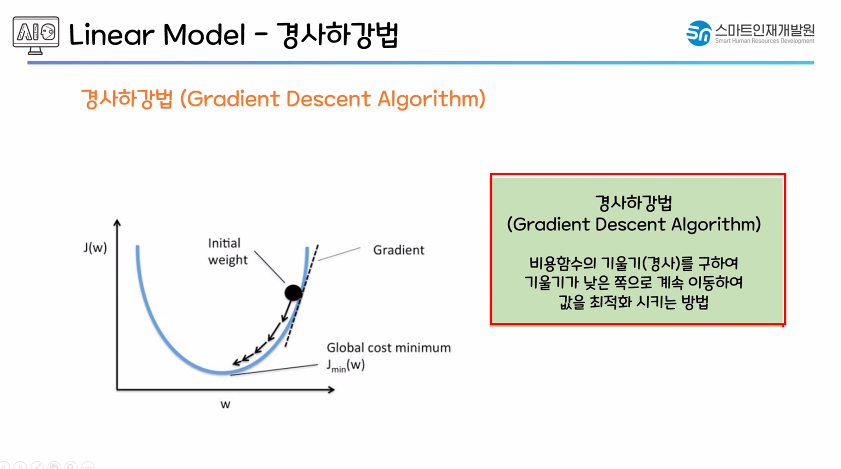
- 경사하강법
- 처음 가중치값(w)을 랜덤으로 지정
- 접선의 기울기가 낮아지도록 만듬.
- 기울기가 낮아질수록 오차값(J(w))이 작아지는 것을 확인 가능함.
(편미분 : 한쪽 방향으로만 진행 - 값이 작아지는 쪽으로만 진행하면 되므로 미분이 아닌 편미분 사용)
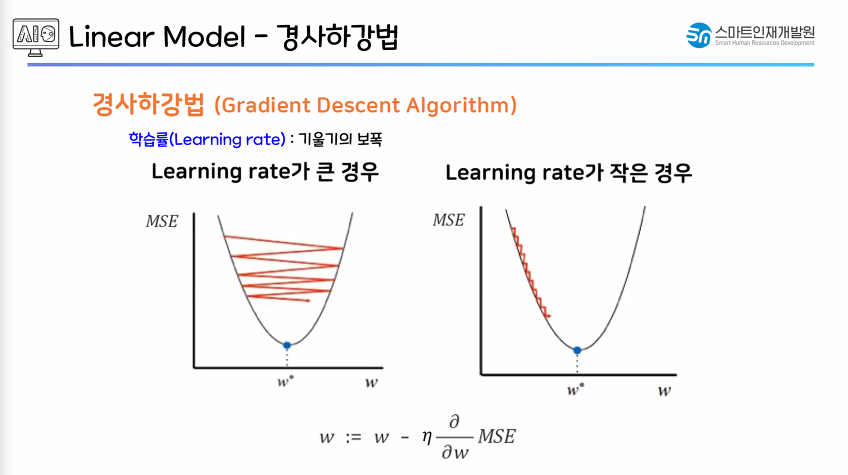
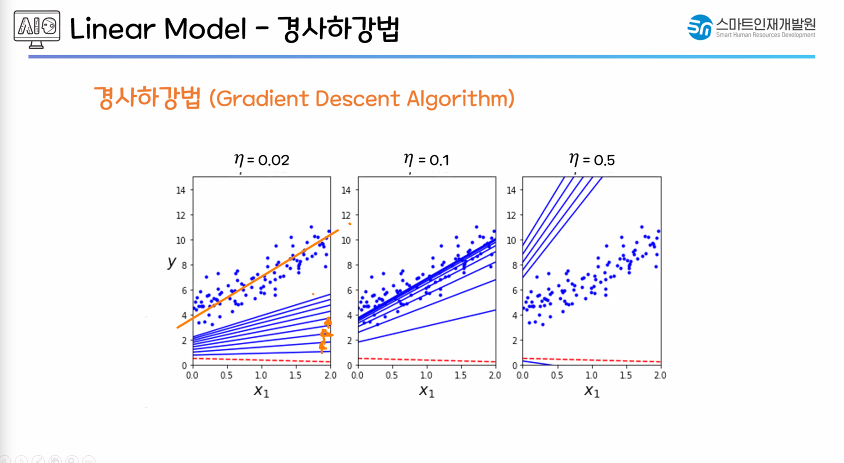
- 학습률(Learning rate) : 기울기의 보폭(보폭 : 기울기를 줄이는 보폭을 얼마로 정할 것 인지)
