• 원문 : https://towardsdatascience.com/dimensionality-reduction-for-data-visualization-pca-vs-tsne-vs-umap-be4aa7b1cb29

  	이 글은 개인적인 공부를 위해 해외 기사를 번역해서 리뷰한 것입니다!

What is Dimensionality Reduction?

• 많은 피처를 가진 머신러닝에서 가장 중요한 문제들:
  • 많은 피처가 training을 굉장히 느리게 만드는 것
  • 좋은 솔루션을 찾기 어렵게 만드는 것
    
    
• Curse of dimensionality (차원의 저주)
  • 차원을 축소하는 것은 하나의 중요한 요소이다.

• Dimenstionality Reduction이 사용되는 곳
  • Data Compression
  • Noise Reduction
  • Data Classification
  • Data Visualization

---

Main Approaches for Dimensionality Reduction

Projection

• 높은 차원의 데이터들을 낮은 차원으로 끌고 오는 것
• 포인트 간의 거리를 대략적으로 보존하는 특징이 있다.

*PCA

Manifold Learning

• training instance가 있는 위치에서 manifold를 모델링하여 차원을 축소하는 방식을 Manifold Learning이라고 부른다.
  -> training instance가 있는 위치라는 게 실제 subspace를 뜻하는 듯

What is Manifold Learning?

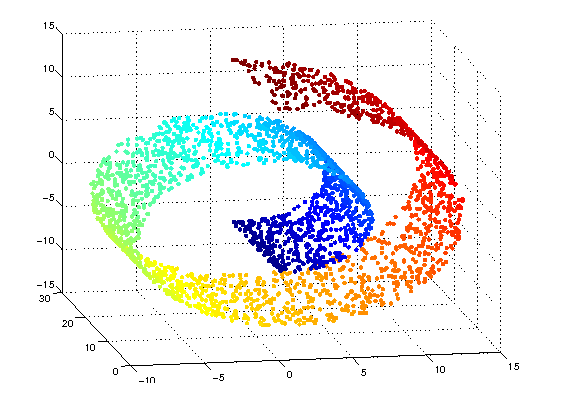
Manifold = 고차원의 데이터
- 고차원의 데이터를 공간상에 표현할 때 찍히는 점들을 아우르는 subspace = Manifold(원본 공간)
- Manifold를 찾는 것 = Manifold Learning
- 잘 찾은 Manifold에서 projection 시키면 데이터의 차원이 축소될 수 있다.
- Manifold 학습 = 학습이 되지 않은 상태에서 데이터를 통해 모델을 학습해 나가는 것.
- 스위스 롤

• Manifold Learning은 Manifold assumption에 기반을 두고 있다.
  

  • Manifold Hypothesis(assumption) in general
    (a) Natural data in high dimensional spaces concemtrates close to lower dimensional manifolds
    : 고차원의 데이터의 밀도는 낮지만, 이들의 집합을 포함하는 저차원의 매니폴드가 있다.
    (b) Probability density decreases very rapidly when moving away from the supporting manifold.
    : 이 저차원의 매니폴드를 벗어나는 순간 밀도는 급격히 낮아진다.

    				reference : https://junstar92.tistory.com/157

• Manifold assumption in semi-supervised learning?
  (a) the input space is composed of multiple lower-dimensional manifolds on which all data lie
  (b) data points lying on the same manifold have the same label
  

• Manifold 학습은 탐색적 데이터 분석에 유용하고, 지도학습에는 사용하지 않기 때문에 semi-supervised로 사용

• 이웃 데이터 포인트에 대한 정보 보존이 가장 큰 목적이다.

*t-SNE

---

PCA(principal Component Analysis)

• for "unsupervised" algorithm
  

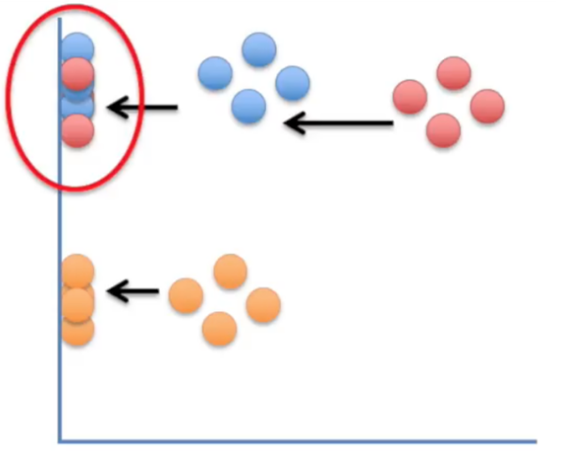
Principal Components

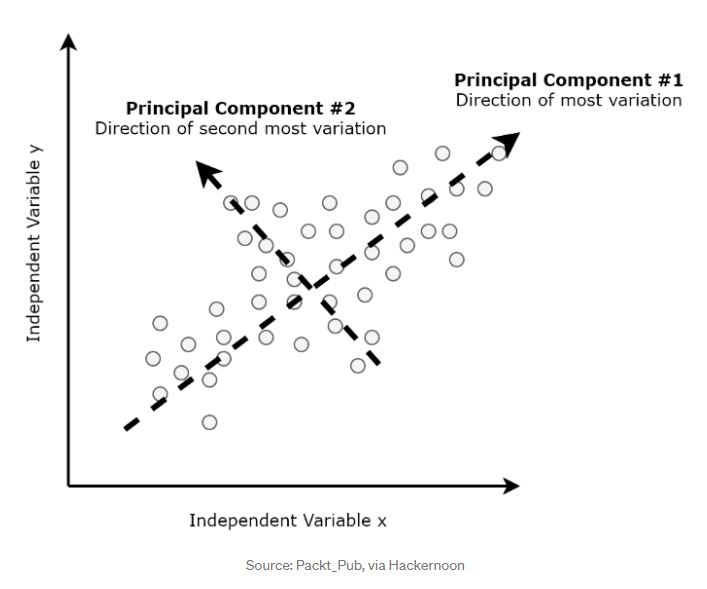
• Principal components: 트레이닝 데이터 안의 최대 variance의 갯수에 대한 축(axis)
  • means finding the First, Second, Third components orthogonal to the other component(s)
  • 각 variance를 하나 축으로 해서 직교하는 애들을 하나씩 그어 나간다는 뜻

---

t-SNE(T-distributed stochastic neighbour embedding)

• high dimensional dataset을 사용한다.
• 하나의 데이터 포인트에 대해 2-3차원으로 된 맵 위치를 제공한다.
• 모든 데이터에 대해 거리를 찍는 게 아니라 데이터 하나에 대해 2-3차원의 거리를 만들어서 그 데이터들의 의미 사이의 cluster를 찾는 것
  • 따라서 데이터 안의 의미를 보존하는 것이 가능하다.
• t-SNE는 비슷한 인스턴스들끼리의 거리를 지키고, 다른 인스턴스를 떨구면서 차원축소한다.

---

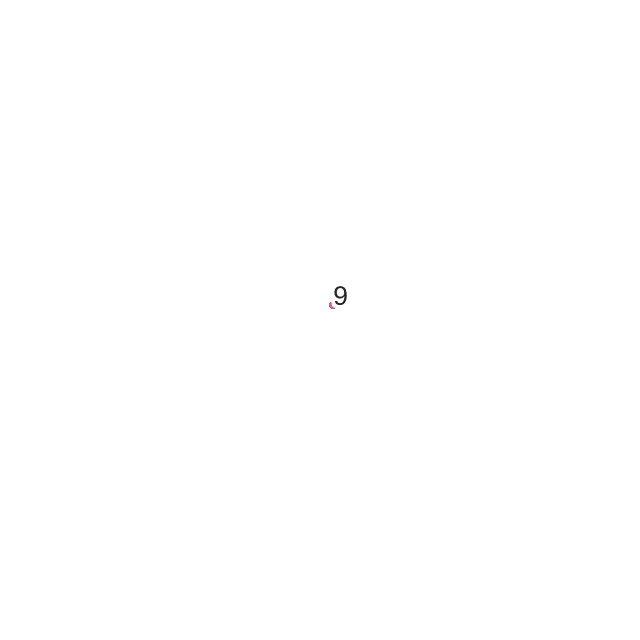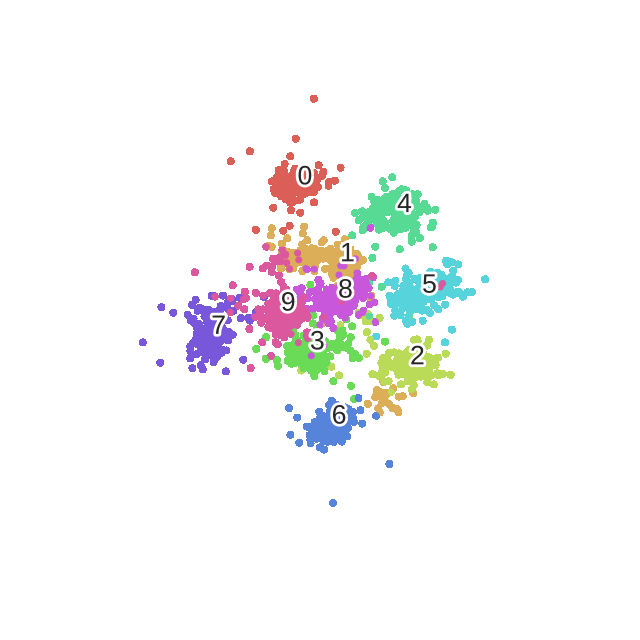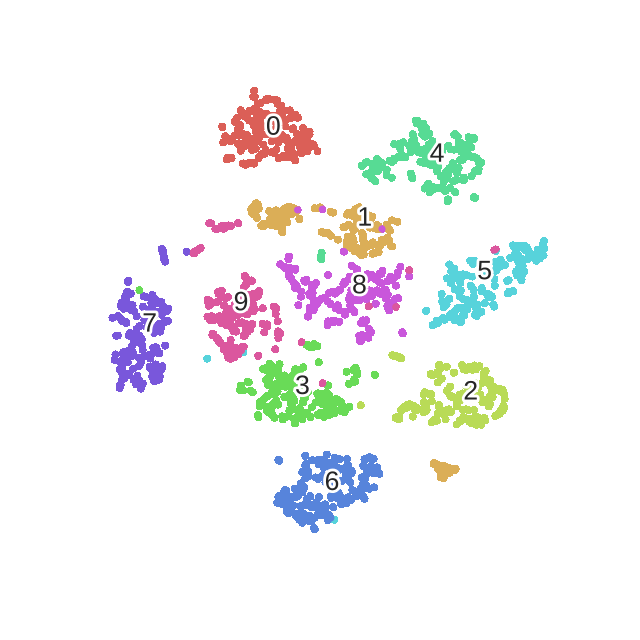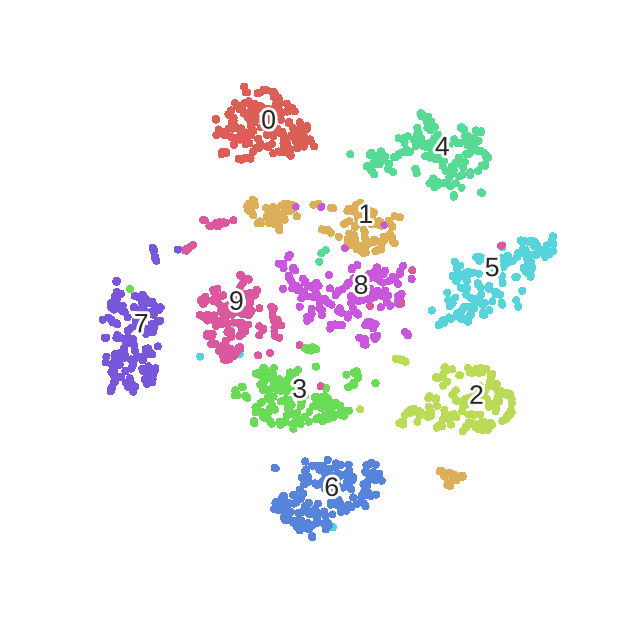
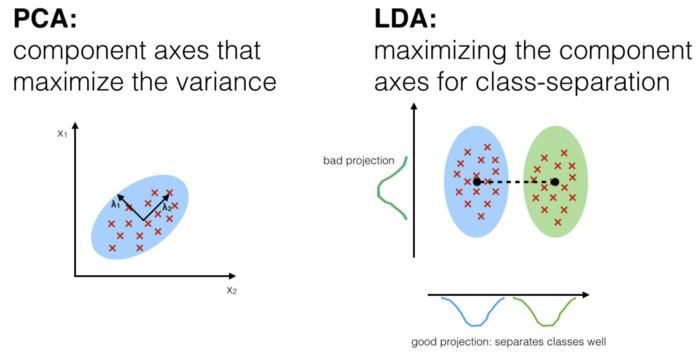
LDA(Linear Discriminant Analysis)

• "supervised" and computes the directions("linear discriminants") seperation maximized
• pattern classification의 전처리 과정에서 주로 사용하는 기법
• 오버피팅과 computational cost를 줄이기 위해서 class-seperability를 좋게 만들려고 고안됨.
  • class-separability: 클래스의 분류 정도(?)로 해석해야 할 것 같다.
• PCA와 비슷하지만 다양한 클래스들간의 분리를 최대화한다는 점에서 차이가 있다.

---

UMAP(Uniform Maniold Approximation and Projection)

• nonlinear dimensionality reduction method
  • effective for visualizing clusterings or groups of data points and their relative proximities
• t-SNE와의 차이 = scalability (확장성)
  • sparse한 matrices에 바로 적용될 수 있다.
  • preprocessing 과정 전에도 적용될 수 있다는 장점이 있음.
• t-SNE와 비슷하지만 더 빠름.