2021.09.01 공부

원문 : https://towardsdatascience.com/5-exciting-deep-learning-advancements-to-keep-your-eye-on-in-2021-6f6a9b6d2406
노션 : https://resilient-jackfruit-555.notion.site/5-Exciting-Deep-Learning-Advancements-in-2021-5b5f758ddc8d40ec84ec1a8a0f47a474

GrowNet

GrowNet Intro.

• 얕은 신경망에 gradient boosting을 적용한 것

• 분류, 회귀, 랭킹에서 굉장한 성과를 보여주고 있음.

• Non-specialized or sequence data (ex. 이미지가 아닌) 데이터에서 이용됨

• GN의 아이디어: weak learner를 앙상블하는 것, 각각의 weak learner들은 이전 weak learner의 실수를 바로잡아 준다. (얇은 레이어를 많이 깔면서 이전 레이어의 오차를 개선하는 방식으로 나아가는 듯?)

• 예시를 보면 모델1, 모델2, 모델3이 이전 모델의 잔차를 이용해서 학습하고, 이 각각의 모델은 심플하지만 전체를 앙상블하면 복잡하게 된다.

• GN 앙상블은 k개의 모델로 이루어져 있으며, 각각의 모델은 original features와 이전 모델의 예측값들에게서 영향을 받음
• 전체 모델들의 예측값을 마지막에 합해서 내놓는데, 하나의 모델은 히든 레이어를 하나밖에 가지고 있지 않을 정도로 굉장히 심플

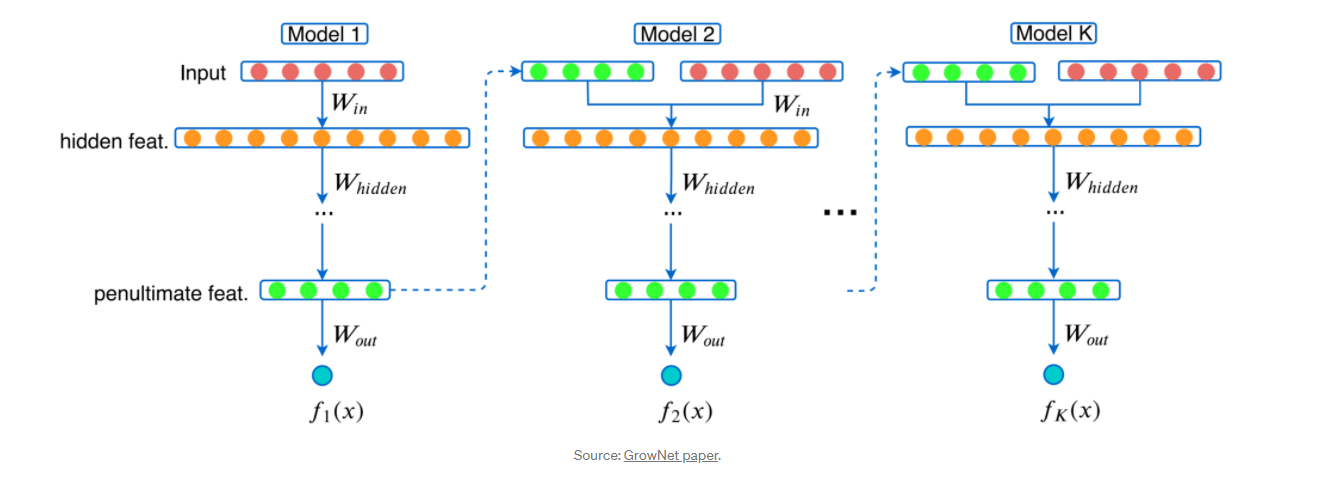
• GN 모델은 계산도 적고, 학습하는 시간도 짧아서 튜닝하기 굉장히 쉬우므로 회귀, 분류, 랭킹에서 엄청 좋은 성과를 내고 있다고 함

(그래서 열심히 자료를 찾았는데 없슴니다 ㅠ_ㅠ)

TabNet

스터디에서 한번 다루었으니 패스

EfficientNet

워낙 유명하니 패스

The Lottery Ticket Hypothesis

The Lottery Ticket Hypothesis Intro.

- NN의 pruning(가지치기)을 설명할 수 있는 하나의 예시 - 아마존에서 펜을 샀는데, 박스 안에 충전재(ex.뽁뽁이)가 가득 들어있고, 그 안에서 작은 펜을 찾는다고 가정하면, 작은 펜을 찾는 동안은 쓸데없는 충전재를 하나하나 확인해야 하는데, 펜을 찾고 나면 충전재는 모두 쓸모가 없게 된다. - 이 상황에서 알 수 있듯, 박스 안에는 pen이라는 real work를 하는 subnet이 있고, 쓸데없고 다양한 neural network들이 존재한다. 우리는 이 '진짜 일'을 하는 subnet을 찾기만 하면 된다! - 하지만 이 subnet을 찾기 위해서는 결국 처음에는 커다란 네트워크가 필요하다는 것.

✔️ 이 많은 것들 사이에서 당첨복권(subnet)을 찾겠다!

Q. 그럼 왜 모델이 클수록 공부가 잘 될까? subnet을 찾기가 더 어려울텐데?!
A. 논문에서는 모델이 클수록 subnet을 찾기가 쉽다고 함. 사람들이 복권을 많이 살수록 복권 당첨되는 사람들이 많아지는 것처럼. 내가 복권을 많이 살 수록 당첨 확률도 높아질 것. 모델이 클수록 subnet을 찾을 수 있는 확률도 높아진다고 보면 될 것 같다.

• Lottery Ticket Hypothesis: 충분히 깊은 모든 신경망 모델 안에는 전체 신경망 모델만큼의 성능을 낼 수 있는 작은 subnetwork가 존재한다.

• Deep Double Descent
  

  • Bias-Variance Trade-Off
    
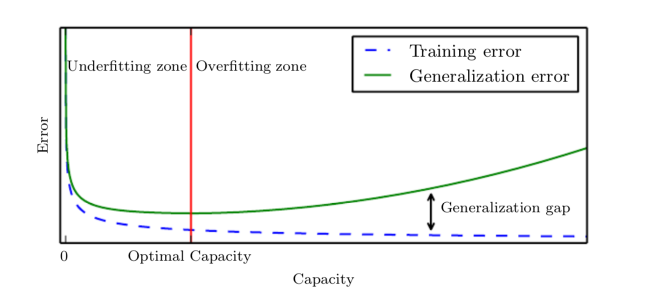
    : 고전 ML의 통념인, 큰 모델(파라미터도 많고, 데이터도 많고, 에폭도 많은)은 Overfitting이 일어나기가 쉽다.를 설명하고자 가져온 그래프
    

  • Model-wise Double Descent
    
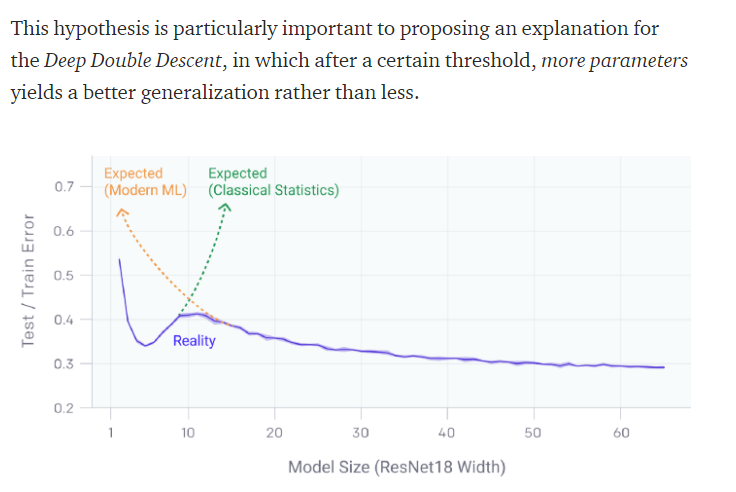
    : Interpolation Threshold를 기점으로 왼쪽은 Bias-Variance Trade-Off를 따르고 있지만, 오른쪽은 파라미터 갯수가 커질수록 성능이 향상되는 모습을 보이고 있다.

    Q. What is Interpolation Threshold?
    A. The interpolation Threshold is the point at which there are the fewest reachable models with zero training error.
    - 근사함수 임계값: 가장 정답에 근사한 함수의 최대값(한계값) : 쉽게 말해, 가장 잘 찾은 값, 가장 근사한 함수에 다가갈 수 있는 한계값

    Q. 아니 그러면 그냥 파라미터 수가 많고 파라미터를 잘 설정했을 수도 있자나?!
    A. Nope!
    - Epoch-wise Double Descent
    
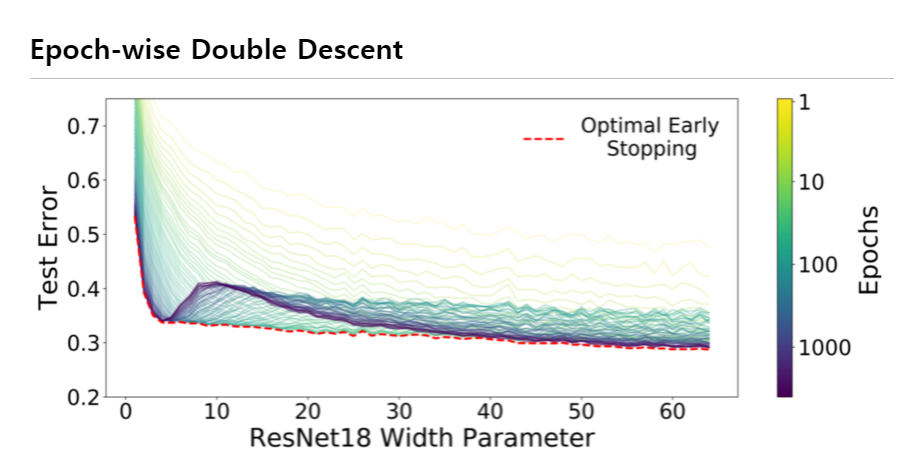
    : Epoch이 많아져도 같은 모습을 보인다. Optional Early Stopping이 최저 Test Error에 도달했다가 다시 그보다 더 낮은 Test Error를 가지게 되는 모습을 볼 수 있다.
    
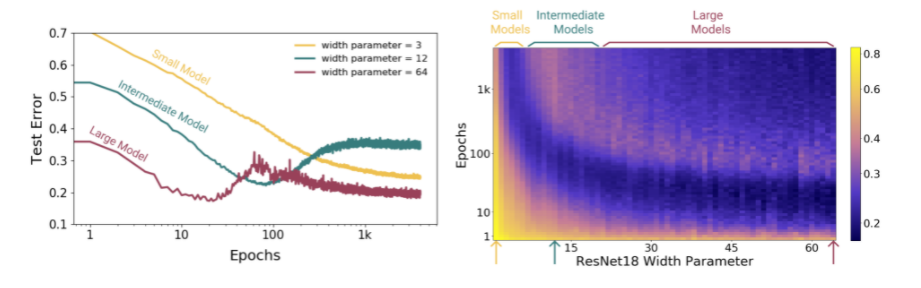
    : 위 현상은 Optimizer나 LR Scheduler를 바꿔도 일어난다.
    
    

∴ 파라미터 외에도 다양한 아이들이 모델의 복잡도와 크기에 영향을 준다. 그리고 큰 모델이 무조건 안좋은 것은 아님! 왜? 모델이 클수록 subnetwork를 찾을 확률이 높아지니까!!

• 후속 논문: 링크텍스트

The Top-Performing Model with Zero Training

The Top-Performing Model with Zero Training Intro.

• 쉽게 말해서, 훈련이 안된 모델이 훈련이 된 모델만큼의 성과를 보인다는 연구 결과가 있다는 이야기
• 앞서 말한 Lottery Ticket Hypothesis와 비슷하게, 신경망 안에 얼마나 많은 정보가 있는지 그냥 찾는 방식이다.

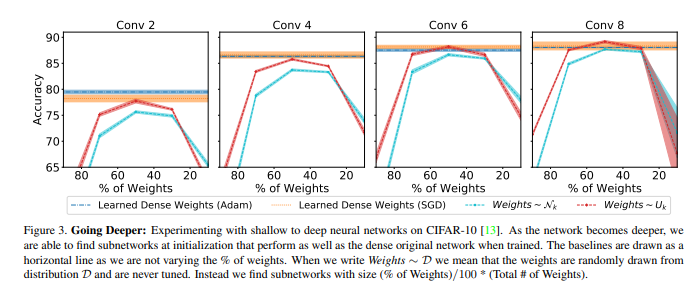
• 이미지 데이터 기준으로, Conv의 갯수를 조금씩 늘릴 수록 Accuracy가 늘어난다.
  - 당연한 거 아니야? 라고 할 수 있겠지만, 훈련 데이터를 지정해주거나 하지 않고 완전히 랜덤한 애들을 뽑았다는 점!
  • 다시 말해, 잘못 뽑으면 성능이 훅 떨어질 수 있는데 그러지 않는다는 것
  • 모델이 커질 수록 앞서 말한 subnetwork를 찾을 확률이 높다는 가설의 근거가 되기도 하고 가설을 적용한 방식이 될 수도 있다는 것!

• 완전히 랜덤한 신경망 모델에서 subnetwork를 찾을 수 있었다는 게 대단하지 않느냐..
• 예시를 들자면, 아무렇게나 막 쓴 알파벳 중에서 우연히 내 이름을 찾은 것과 같다.

• 하지만 이 모델은 아직 연구중이고, 모르는 부분이 너무 많아서 answer보다는 question이 더 많은 상태임을 인지해 두라고 마지막에 말하고 끝난다...

• 논문 원문
  링크텍스트