TPS Jan 데이터를 받아다가 구경했는데
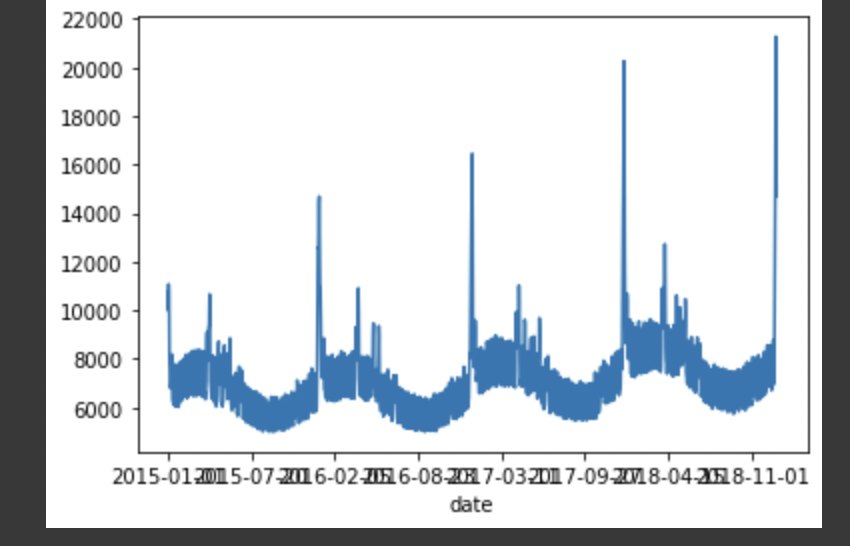
날짜로 groupby를 했더니 데이터가 이렇게 생겨서 당황했다
생겨먹은 게 시계열 데이터 스타일이라는 건 알겠는데, 시계열 개념 자체에 대한 이해가 별로 없어서 모델 이름은 아는데 언제 어떻게 쓰는건지도 모르겠고
그래서 모델에 데이터를 적용하기 위해 아주 간단히만 시계열 기초와 시계열 모델에 대해 공부해보고자 한다.
그래서 오늘은 구글링으로 시계열 무근본 공부하기 ✨
시계열 예측(Time-Series forecasting)?
시계열은 일정 시간 간격으로 배치된 데이터들의 수열을 말한다. 시계열 해석(time-series analysis)라고 하는 것은 이런 시계열을 해석하고 이해하는 데 쓰이는 여러 가지 방법을 연구하는 분야이다.
시계열 예측이라고 하는 것은 주어진 시계열을 보고 수학적인 모델을 만들어서 미래에 일어날 것들을 예측하는 것을 뜻한다.
시계열 데이터를 분석하는 수학적 모델은 여러가지가 있을 수 있는데, 실제 응용에서 가장 많이 쓰이는 세 가지 범용 모델은 AR, I, MA 모델 등이 있다. 이 세가지 방법은 이미 얻어진 시계열 데이터에 선형 종속적이다. 비선형 종속적인 방법들은 나름대로 의미있는 것들이 있는데, 예컨대 혼돈 시계열 등을 만들어낼 수 있기 때문이다.
- https://ko.wikipedia.org/wiki/%EC%8B%9C%EA%B3%84%EC%97%B4
Basics of Time-Series Forecasting

시계열 예측 태스크에서 중요한 것은 세가지의 포인트임
1) Seasonality

한국어로 해석하면 계절 변동성쯤 되나,,
계절 변동성이란 시계열 데이터 내에 다른 시기들과 뚜렷하게 비교되는 몇 시기(달)이 존재한다..인데
다른 말로 하면 어느 기준에 따라 계속해서 반복되는 시즌이 있다는 것이다.
본문에서는 예시로 3년간의 여행 데이터에서 11월과 12월이 휴가 및 축제 시즌이기 때문에 여행자 분포가 굉장히 높다는 사실을 발견했다는 점을 들었다.
이런 게 바로 Seasonality (계절 변동성)이며, 시계열을 예측할 때는 이 계절 변동성을 포착하는 것이 중요하다.
2) Trend

trend(추세)란 확실히 올라가거나 내려오는 트랜드(예?)를 가진 시기가 있다는 것이다.
어느 시기 + seasonality 가 증가하거나 감소하는 것과 비슷한 맥락이라고 생각해볼 수 있음.
으에? 먼소리여 한국어로 해석하기가 힘드네계절적 변동성 + 알파 -> 어느 트랜드
이런 느낌으로 이해
3) Unexpected Events

unexpected events란 예측될 수 없는, 혹은 잡을 수 없는 동적인 변화들이 일어나는 것을 뜻한다.(한국어로 만드는 걸 포기하기로 함)
예를 들어서 코로나는 예측하지 못한 상황이기에, 일부 회사 주가의 엄청난 감소를 불러왔다. 이런 것
Result
seasonality와 trend는 어느 정도 예측이 가능한 부분이지만, unexpected events는 예측하기가 매우 힘들다는 특징이 있다.
reference: https://www.analyticsvidhya.com/blog/2021/07/time-series-forecasting-complete-tutorial-part-1/Additive and Multiplicative Time Series
Additive Time Series
Additive Time Series란 trend(T), seasonality(S), irregularity(I) 의 덧셈(addition)이다.
Multiplicative Time Series
반면에 Multiplicative Time Series란 trend, seasonality, irregularity 세 요소의 곱셈(multiple)이다.
Time Series Exponential Smoothing
지수 평활법.. 태블로할 때 한번 들어봤다..ㅎ,,,
지수 평활법은 과거 값들의 평균을 내는 방식인데, 과거 값의 빈도에 따라 가중치를 다르게 주고, 현재의 값일수록 가중치를 더 많이 준다는 특징이 있다.
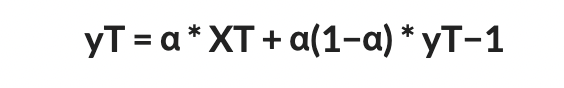
수식은 이허라다... 이후는 코드 베이스의 설명이므로 넘어가도록 한다...ㅎㅎ..
규칙적 시계열 분석과 불규칙적 시계열 분석
시계열 분석은 크게 규칙적과 불규칙적 시계열 분석으로 나뉜다.
규칙적 시계열이란 트랜드와 분산에 큰 변화가 없는 데이터를 말하고, 불규칙적 시계열이란 앞서 말한 바와 같이 트랜드가 변화하는 것을 말한다.
이 불규칙한 시계열 데이터를 규칙성을 부여하여 분석을 하는 게 바로 AR, MA, ARMA, ARIMA 방법이라고 볼 수 있다.
RNN 중의 하나인 LSTM은 이전 상태를 꽤 오래 기억하면서 순환적인 네트워크의 파라미터를 자동으로 학습하는 모델이다.
NLP 공부를 할 때 이전 값의 영향을 받으면서 학습해서 언어적인 학습이 가능하다는 기초 이론을 접한 적이 있는데, 이전 값의 영향을 받는 건 역시 시계열 데이터도 마찬가지이므로 비슷한 맥락에서 공부할 수 있지 않을까 싶다.
reference: https://yamalab.tistory.com/112다양한 모델들
AR 모델
AR 모델(Auto Regression), 다른 말로 자기회귀모델이라고 한다.
자기 자신의 과거를 사용하기 때문에 이런 이름이 붙었다.
이전에 모델 자신이 관측한 값이 이후 자신이 관측할 값에 영향을 준다는 것.
RNN이랑 진짜 비슷하네..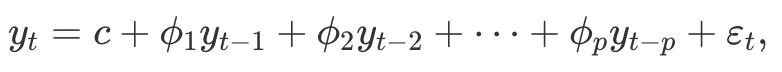
출처: https://otexts.com/fppkr/AR.html여기에서 제일 마지막에 더해주는 값은 white noise라고 한다.
앞서 Yt-1에서 보이듯이 자기 자신의 이전 값에 영향을 받는다.
이 모델은 과거에 기반해서 미래를 예측하기엔 매우 적절하지만, 과거의 데이터와 관련이 적게 트랜드가 변동하는 경우(사실은 모르는 거겠지만..)에는 부적절하다고 한다.
이 경우 MA(Moving Average)모델을 사용할 수 있다.
MA 모델
MA(Moving Average) 모델은 트랜드가 변화하는 상황에서 적합하다.
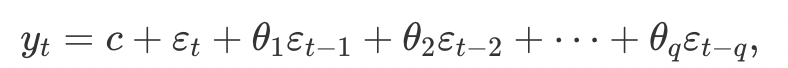
출처: https://otexts.com/fppkr/MA.html여기서도 마찬가지로 white noise가 존재한다.
앞서 말한 AR모델과 다르게, MA모델은 과거에 예측했던 값의 오차를 통해 학습한다는 점이 다르다.
오차값을 반영한다는 건, 변화하는 값을 반영한다는 것이므로 이전 값 자체를 반영하는 것보다 트랜드에 민감하다고 이해하는 정도이면 되지 않을까 싶다.
평균 평활과 헷갈리지 말자. 이동 평균 평활은 과거 값의 추세를 통해 주기를 예측할 때 사용하고, 이동 평균 모델은 미래 값을 예측할 때 사용한다는 점을 알아야 할 것 같다.
ARMA모델
이제 앞서 언급한 AR과 MA모델을 합한 ARMA라는 모델에 대해서 공부한다!
즉, 과거의 값 자체와 그 과거 값의 오차값을 통해 현재 값을 예측한다.
실제로 이렇게 더했을 때 분석의 정확도가 꽤 많이 올라간다고 한다.
AR, MA 두 가지 관점에서 1 윈도우 이전만큼의 과거를 참고하는 것을 ARMA(1,1) 모델이라고 하고, 2윈도우 이전을 참고하는 것을 ARMA(2,2) 모델이라고 한다.
참고: 윈도우?
sliding window 알고리즘에서 이 윈도우라는 의미를 찾을 수 있을 것 같다.
전체 길이에서 어느 정도의 길이를 잘라서 이 길이만큼을 윈도우라고 하는 것 같은데, 예를 들어
( 1, 2, 3, 4, 5) 의 값을 가진 리스트가 있을 때 길이가 3인 subset을 찾아보면,
(1,2,3) (2,3,4) (3,4,5) 가 나올 수 있다. 이때 이 subset 하나를 윈도우라고 할 수 있을듯!
reference: https://undeadkwandoll.tistory.com/45
ARIMA 모델
앞서 말한 ARMA에서 가운데에 Intergrated라는 개념을 추가한 모델이다. 다른 말로 비-계절성(non-seasonal) ARIMA 모델이라고도 표현하는 것 같다. (이동평균을 누적한 자기회귀)
ARMA가 과거의 데이터를 사용하는 것에 반해 ARIMA는 거기에 그 데이터가 지니고 있는 trend까지 반영한다고 생각하면 된다고 한다. (Correlation + Cointegration)
정확히 말하자면 ARIMA 모델은 관측치 사이의 차분(Difference)라는 개념을 사용하여 불규칙적 데이터를 규칙적 데이터로 활용할 수 있도록 하는 과정을 거친다는 것.
reference: https://yamalab.tistory.com/112차분(Difference)? 추가로 정상성(stationarity)?
정상성(stationary)
정상성을 나타내는 시계열은 시계열의 특징이 해당 시계열이 관측된 시간에 무관하다.
따라서, 추세나 계절성이 없는 시계열이 정상성을 나타낸다고 볼 수 있다. - 추세(아마 trend겠지)와 계절성은 서로 다른 시간에 시계열에 값에 영향을 주기 때문..(trend와 seasonality는 계속해서 전체 시계열 데이터에 영향을 주기 때문임(ex. 매년 여름에 아이스크림이 잘 팔린다) ,,정도로 해석하면 더 좋을 것 같다.)
반면에, white noise는 정상성을 나타내는 시계열이다. 왜냐햐면, 언제 관찰하는지에 상관이 없고, 어떤 시점에서 보더라도 똑같이 보이기 때문에. (아까 수식에서 더해준 것.)
차분(Difference)
차분은 정상성을 나타내지 않는 시계열을 정상성을 나타내도록 만드는 방법. - 연이은 관측값들의 차이를 계산하는 것
차분은 시계열의 수준에서 나타나는 변화를 제거하여 시계열의 평균 변화를 일정하게 만드는 데 도움이 될 수 있다. 결과적으로 추세나 계절성을 제거(또는 감소)하는 역할을 한다고 볼 수 있다.
정상성을 나타내지 않는 시계열을 찾아낼 때 데이터의 시간 그래프를 보는 것만큼, ACF 그래프도 유용함.
정상성을 나타내지 않는 데이터에서는 ACF가 느리게 감소하지만, 정상성이 있으면 ACF가 비교적 빠르게 0으로 떨어지기 때문. - ACF는 뒤에서 다시!
ARIMA 모델은 자기 자신의 추세만 고려하기 때문에 white noise의 추세는 고려하지 않으며, 사람들은 ARMA 모델과 비슷하다고 생각해서 선호하지 않는다고 한다.. 어디서 보니 ARMA 모델이 연구자들에게 많은 사랑을 받는다고 하더라..그래서 그런가 8ㅁ8
reference: https://continuous-development.tistory.com/235#1.%EC%9E%90%EA%B8%B0%EC%83%81%EA%B4%80(Autocorrelation)%20-%20AR%20%EB%AA%A8%ED%98%95추가: 시계열에 관한 학문에서는 데이터의 trend와 seasonality를 제거해서 whitening 시킨다고 표현하는 것 같다. white noise가 trend와 seasonality에 영향을 받지 않는 것인 것처럼..?
이 ARIMA 모델은 차수가 결정되어야 하는데, 이 차수가 달라짐에 따라 ARIMA(p,d,q)가 구성된다고 한다.

이 차수를 찾아내는 것으로 아까 만난 ACF(Auto-Correlation Function, 자기 상관 함수), PACF(Partial Auto-Correlation Function, 편 자기 상관 함수)를 사용하게 된다고 한다. 밑에서 공부해보자.
출처: https://otexts.com/fppkr/non-seasonal-arima.htmlSARIMA
앞서 설명한 (non-seasonal) ARIMA 모델에 계절성을 추가한 Seasonal ARIMA 모델도 존재한다.
seasonality를 가지고 있기 때문에 데이터의 주기(계절이니까 계절에 맞게 주기가 추가된다는 것 같다.)를 설정해주면서 SARIMA 모델을 사용할 수 있을 것 같다.
SARIMA에서의 파라미터를 결정해주기 위해서는 다른 방법을 통해 차분을 수행한다고 한다.
(.......이건 이렇게만 알고 넘어가자...)
- reference: https://techblog-history-younghunjo1.tistory.com/98ACF와 PACF
ACF
ACF(Auto-Correlation Function), 자기 상관 함수는 어떤 신호의 시간이동된 자기자신과의 상관성(Correlation) 척도
k 시간 단위로 구분된 시계열의 관측치간 상관의 측도
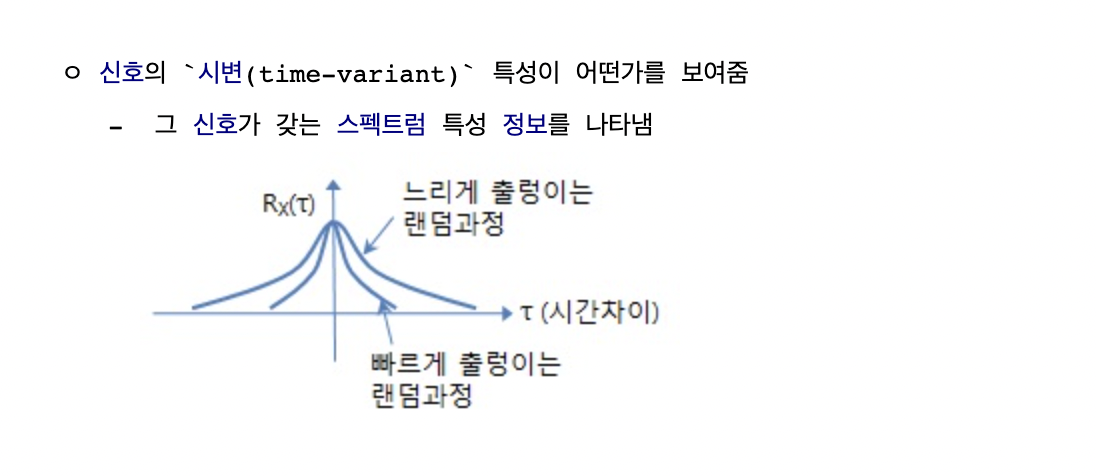

....예? 머라구여..?
출처: http://www.ktword.co.kr/test/view/view.php?m_temp1=3547그냥 쉽게 이해한 바로는, 시간에 따라 변화하는 특성이 어떤가를 알려주는 건데,
시간이 바뀌면서 변화하는 값들이 서로 어느정도 상관관계가 있냐라는 걸 계산하는 게 자기상관함수라는 걸로 이해했다. 그러니까 그냥 시간이 변화하는 거랑 값이 변화하는 게 관계가 있냐!!!! 아까 정상성 이야기할 때 나왔던 개념과 비슷한 것 같은데!!!!!!!😵💫
출처: https://otexts.com/fppkr/graphics-autocorrelation.html- 데이터에 trend가 있을 때, 작은 시차(짧은 시기)에 대한 자기상관은 큰 양의 값을 갖는다.
- 시간적으로 가까운 관측치들이 값의 크기도 비슷하기 때문. (y=x 생각하면 쉬울듯)
- 그래서 trend가 있는 시계열의 ACF는 양의 값을 가진다. (아까 정상성 이야기할 때!! ACF와 정상성 확인하는 방법에서!!! 아하!!! 희열🤓)
- seasonality가 있을 때는 계절성 시차의 경우에 더 크게 나타난다.
- trend와 seasonality를 모두 나타낼 때는 이거 두개가 다 나타난다. 대환장파티 ;ㅅ;
reference: https://otexts.com/fppkr/graphics-autocorrelation.htmlPACF
PACF(Partial Auto-Correlation Function), 편자기함수는 다른 모든 짧은 시차 항에 따라 조정한 후 k시간 단위로 구분된 시계열의 관측치 간 상관의 측도입니다.
예...?.....ㅠ_ㅠ편자기상관함수는 자기상관성을 파악하되, 한 시점과 그 시점으로부터 k 시점 이전의 값, 딱 둘 사이의 관계를 파악하고 그 사잇값들의 영향을 제거하고자 하는 것이다.
reference: https://freshrimpsushi.github.io/posts/pacf-partial-autocorrelation-function/아래의 설명이 조금 더 와닿는 것 같다. 구글에도 많이 자료가 없다.
minitab의 독스에서 설명하는 그림을 첨부한다. 이걸 보면 그냥 자기상관함수에서 k시간 단위로 구분된 것이기 때문에 partial을 붙여줬다고 생각하면 될 것 같다. (미니탭 오랜만이네..안녕..?)
자기상관함수
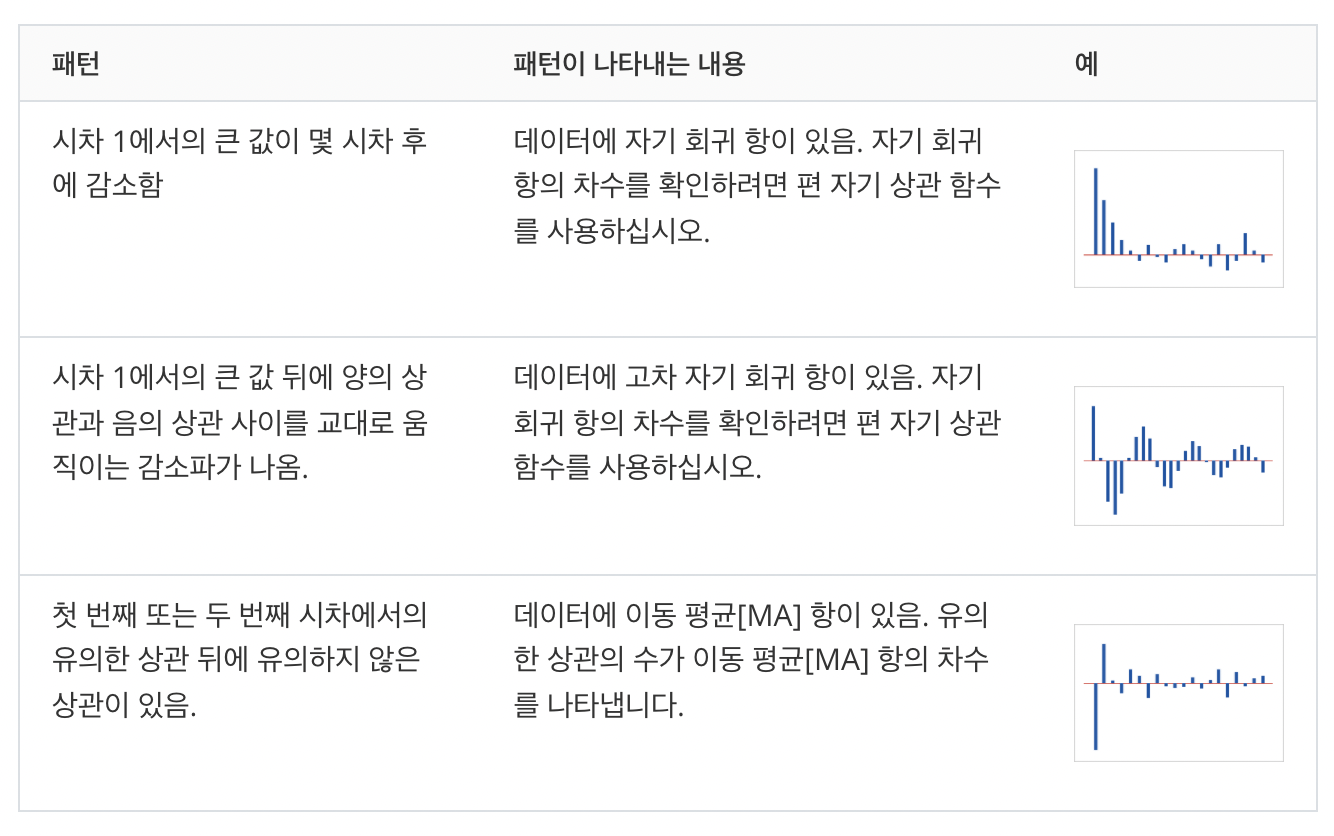
partial 자기상관함수 ⬅️ 편- 보다 이게 조금 더 직관적인듯
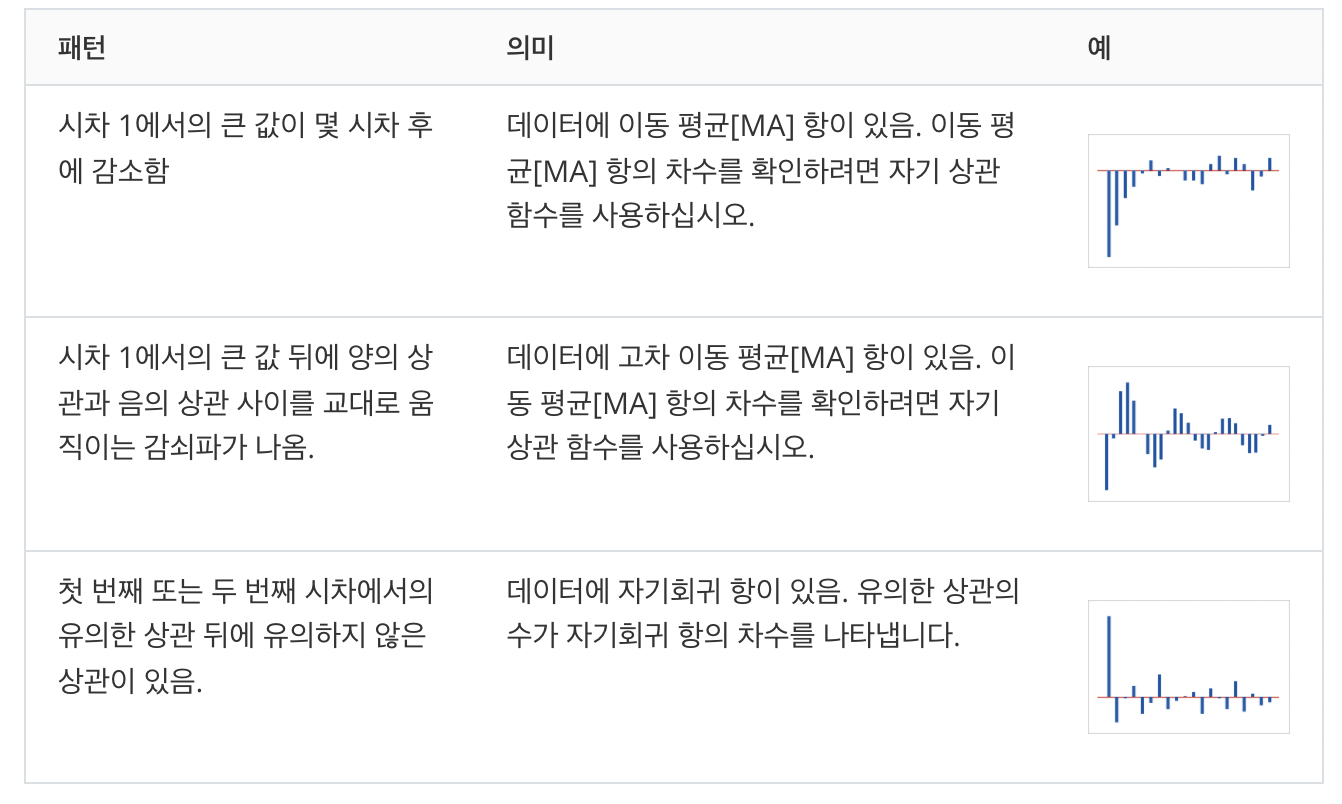
출처 및 reference:
https://support.minitab.com/ko-kr/minitab/18/help-and-how-to/modeling-statistics/time-series/how-to/autocorrelation/interpret-the-results/autocorrelation-function-acf/
https://support.minitab.com/ko-kr/minitab/18/help-and-how-to/modeling-statistics/time-series/how-to/partial-autocorrelation/interpret-the-results/partial-autocorrelation-function-pacf/추가) White noise
백색 잡음(white noise), 앞서서 계속 말했고, 이미 이해하고 넘어간 부분이지만 나중에 다시 읽을 나는 기억이 안날거기 때문에 추가해본다. (안녕? 공부좀해^^)
말했다시피 white noise는 trend나 seasonality를 가지고 있지 않다.
따라서 이를 제거해주는 게 whitening이라는 말로 불리기도 한다는 것 같다.
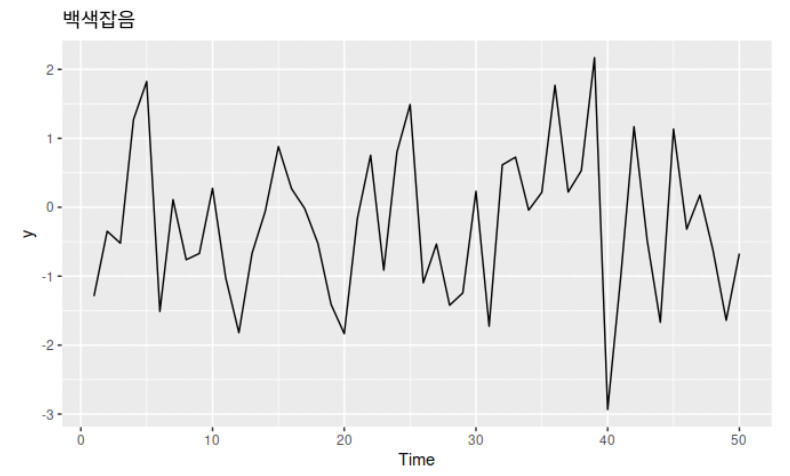
데린이인 나는 뭔가 보이는 것 같다는 착각을 한다..^^ 아이고 데린아..
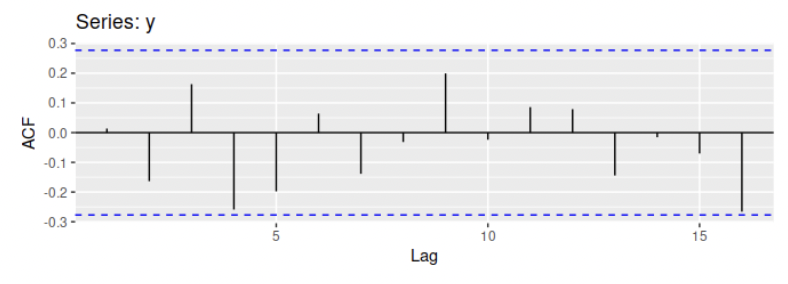
위의 그래프는 백색잡음 시계열 그래프이고, 아래 것은 백색잡음 시계열에 대한 자기상관함수이다. 앞에서 공부한 ACF!
아까 trend가 있으면 ACF가 강한 양의 값을 가진다고 했는데 그래서 강한 양의 값이 보이지 않는 것 같다.
출처: https://otexts.com/fppkr/wn.html솔직히 LSTM도 하고 싶은데 구글링을 통해 시계열 공부만 꼬박 하루 하고 글만 점심먹고 꼬박 5시간째 쓰고있어서 힘들어 죽을 것 같다 이제 좀 쉬자.. 8ㅁ8
