[백준] 1039번 교환

🔔 문제

0으로 시작하지 않는 정수 N이 주어진다. 이때, M을 정수 N의 자릿수라고 했을 때, 다음과 같은 연산을 K번 수행한다.

• 1 ≤ i < j ≤ M인 i와 j를 고른다.
• 그 다음, i번 위치의 숫자와 j번 위치의 숫자를 바꾼다. 이때, 바꾼 수가 0으로 시작하면 안 된다.
• 위의 연산을 K번 했을 때, 나올 수 있는 수의 최댓값을 구하는 프로그램을 작성하시오.

입력
첫째 줄에 정수 N과 K가 주어진다. N은 1,000,000보다 작거나 같은 자연수이고, K는 10보다 작거나 같은 자연수이다.

출력
첫째 줄에 문제에 주어진 연산을 K번 했을 때, 만들 수 있는 가장 큰 수를 출력한다. 만약 연산을 K번 할 수 없으면 -1을 출력한다.

⏱ 시간복잡도

O(N) = N

🎯 풀이방법

핵심포인트

1. K번 수행했을 때 최댓값을 구하는 것이다. 중간에 구하는 최댓값은 중요하지 않다.
2. 같은 수이더라도 교환할 수 있다.
   
   

예시) N=132, K=3

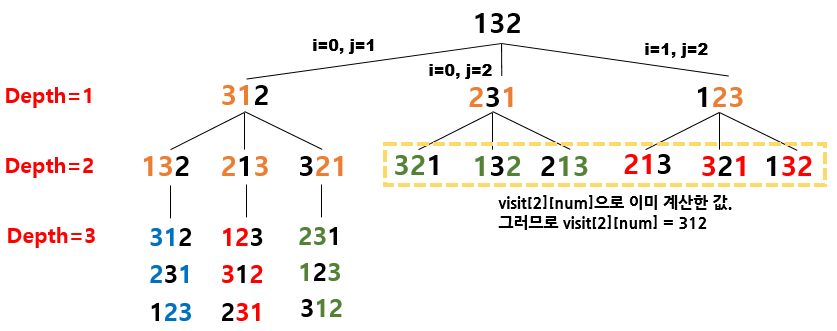
depth=3에 도달하면 현재 숫자를 리턴한다.
depth=2의 경우, visit[3][num] 중 가장 큰 값을 visit[2][num]에 저장한다. depth=1도 동일한 과정을 거친다.

🙄 놓쳤던 점

처음 잘못 생각한 것이 1단계씩 연산을 수행할 때마다 j가 가리키는 값들 중 가장 큰 값을 골라 최댓값을 만들자!이다. 그래서 내가 생각한 로직으로 예시를 계산하면 정답과 예측값이 달랐다. 그러므로 중요한 포인트는 K번 수행한 결과들 중 최댓값을 구한다는 점이다.

💡 이 문제를 통해 얻어갈 것

DFS와 DP를 접목해서 접근하면 해결책이 보인다.

💻 Java 코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

// 백준 1039번 교환

public class Main {
	static int K,len,sol;
	static String N;
	static int[][] visit;  // [변경횟수][최대숫자]

	public static void main(String[] args) throws Exception {
		// 1. 입력
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		N = st.nextToken();
		K = Integer.parseInt(st.nextToken());
		
		len = N.length();
		visit = new int[K+1][1000001]; // [변경횟수][최대숫자]
		
		sol = -1; // 연산 불가능
		sol = dfs(N,0);
		
		System.out.println(sol);
	}
	
	// i,j 위치를 바꿔줌
	static String swapLoc(String str, int i, int j) {
		char[] chars = str.toCharArray();
		char tmp = chars[i];
		chars[i] = chars[j];
		chars[j] = tmp;
		return String.valueOf(chars);
	}
	
	static int dfs(String strN, int depth) {
		int num = Integer.parseInt(strN); 
		if(depth == K) {
			//System.out.println(num + " - depth : "+depth);
			return num;
		}
		
		int ret = visit[depth][num];
		
		// 같은 depth에서 방문한 이력이 있으면 메모지에이션 된 값 리턴
		if(ret != 0)
			return ret;
		
		// 처음 방문한 경우, 안된다고 가정하고(-1) 시작
		ret = -1;
		for(int i=0; i<len-1; i++) {
			for(int j=i+1; j<len; j++) {
				// 0을 맨 앞으로 가져올 수 없음
				if(i==0 && strN.charAt(j)=='0')
					continue;
				
				String tmpStr = swapLoc(strN, i, j);
				
				int tmpRet = dfs(tmpStr, depth+1);
				if(tmpRet > ret) {
					ret = tmpRet;
				}
			}
		}
		
		visit[depth][num] = ret;
		return ret;
	}
}