[백준] 11057번 오르막수

🔔 문제

오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다. 예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다. 수의 길이 N이 주어졌을 때, 오르막 수의 개수를 구하는 프로그램을 작성하시오. 수는 0으로 시작할 수 있다.

입력
첫째 줄에 N (1 ≤ N ≤ 1,000)이 주어진다.

출력
첫째 줄에 길이가 N인 오르막 수의 개수를 10,007로 나눈 나머지를 출력한다.

⏱ 시간복잡도

O(N) = N

🎯 풀이방법

DP 문제이며, 해당 2차원 배열을 구성할 때 아래의 기준으로 설계한다.

• row : i, 1~N까지의 자릿수 (i번째)
• col : j, i번째의 현재 숫자 (0~9)
• dp[i][j] : i번째 자릿수가 가리키는 값이 j일 때 만들 수 있는 오르막 수의 개수

예를 들어, N=5일 때의 dp 테이블이다.

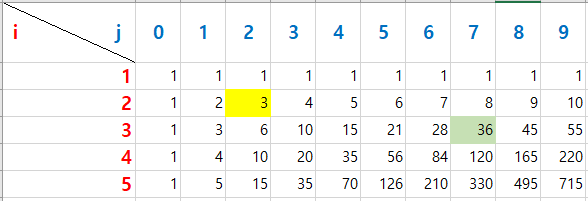
노란색 칸의 의미는 " ❓ 2 "인 경우의 수이다. 즉, 2번째 자릿수가 가리키는 값이 2일 때 만들 수 있는 오르막 수의 개수이다. 다른 예시로 초록색 칸의 의미는 "❓ ❓ 7"인 경우의 수이다. 즉, 3번째 자릿수가 가리키는 값이 7일 때 만들 수 있는 오르막 수의 개수이다. 결과적으로 길이가 N인 오르막 수의 개수를 구할려면 N행의 dp[i][j]의 총 합이 정답이다.

1. 길이가 1인 경우(=dp[1][j])는 1이다.
2. j가 0이면(=dp[i][0]) 1이다. 무조건 0, 00, 000, 0000 밖에 안되기 때문이다.
3. 점화식 : dp[i][j] = dp[i-1][j] + dp[i][j-1]

• ex) dp[3][2] = dp[2][2] + dp[3][1]
  

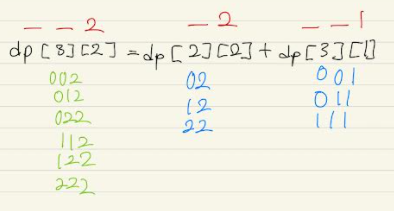
🙄 놓쳤던 점

길이가 N인 오르막의 개수를 10007개로 나눈 나머지를 출력한다. 라는 제한조건을 까먹었었다. 총합을 구할 때나 dp[i][j]를 구할 때도 10007을 나눠줘야 한다.

💡 이 문제를 통해 얻어갈 것

최소 5 step까지 dp를 직접 적어본 후 점화식을 발견하자!

💻 Java 코드

import java.io.BufferedReader;
import java.io.InputStreamReader;

public class Main {
	static int N;
	static long[][] dp; 
	static long answer=0;
	
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		// 1. 입력
		N = Integer.parseInt(br.readLine());
		
		// 2. dp[i][j]- i:N(자릿수), j:현재숫자
		dp = new long[N+1][10];
		
		// 초기화
		for(int i=0; i<10; i++)
			dp[1][i] = 1;
		
		if(N<=1) {
			answer = getSum();
			System.out.println(answer);
			return;
		}
		
		// 3. dp[i][j] : i = step, j = 0~9 현재 step이 가리키는 숫자
		for(int i=2; i<=N; i++) {
			for(int j=0; j<=9; j++) {
				if(j==0) {
					// 3-1. 경우의 수 1개. 무조건 0, 00, 000, 0000 밖에 안되기 때문에,,,
					dp[i][j] = 1;
				}
				else {
					// 3-2. 점화식 dp[i][j] = dp[i-1][j] + dp[i][j-1]
					dp[i][j] = (dp[i-1][j]+dp[i][j-1])%10007;
				}
			}
		}
		
		// 경우의 수 모두 합하기
		answer = getSum();
		System.out.println(answer);
	}
	
	// 모든 경우의 수 합 구하기
	static long getSum() {
		long answer = 0;
		for(int j=0; j<=9; j++) {
			answer += dp[N][j];
		}
		answer %= 10007;
		return answer;
	}
}