[백준] 11438번 LCA 2

🔔 문제

https://www.acmicpc.net/problem/11438

🎯 풀이방법

⭐ LCA

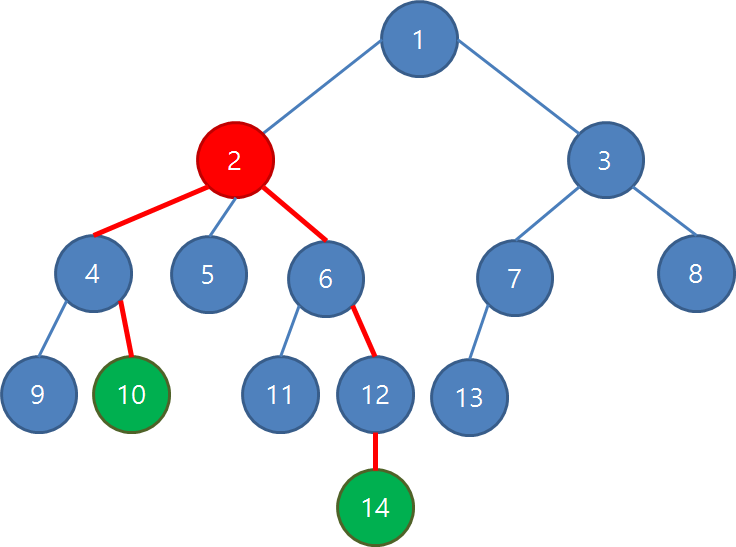
Tree 상에서 두 정점 u,v가 있을 때, u의 조상이면서 v의 조상인 노드들 중 가장 첫번째 공통 조상을 찾는 것이다. 아래의 예시에서, 10번과, 14번의 LCA는 2번이다.

✔ 희소 테이블 : parent
parent[K][V]는 정점 V의 2^K번째 조상 정점 번호를 의미한다. 이 희소 테이블을 사용하면 정점을 건너뛰는 것을 좀 더 빨리할 수 있다. 위의 그래프를 parent 배열로 나타내면 다음과 같다.

✔ 점화식
2^K = 2^(K-1) + 2^(K-1)이므로, 다음과 같은 점화식을 구할 수 있다. 이렇게 k=i-1일 때의 정보가 있다면 k=i일 때의 정보를 얻을 수 있으므로, Bottom-Up방식의 DP를 사용하여 parent 테이블을 채울 수 있다.

parent[K][V] = parent[K-1][parent[K-1][N]]

✔ LCA를 찾는 방식
1. 깊이를 맞추기 위해, depth[u] > depth[v]일 때, u를 parent[u]로 대체하는 것을 반복한다.
2. depth를 맞췄는데 노드가 같다면 종료한다.
3. K를 큰 값부터 순회하여 parent[K][u]!=parent[K][v]라면 u,v를 동시에 2^K만큼 위로 이동한다.

psedu-code

1. LCA 관련 변수, TREE를 할당하고 K를 설정한다.
2. 각 노드의 depth를 DFS로 확인한다. 루트는 늘 1번 노드이다.
3. 희소 테이블인 parent 배열의 값들을 채운다. (점화식)
4. LCA 찾는 방식을 수행한다.
   
   

💡 이 문제에서 알게된 점

• 희소 테이블 (parent)
• LCA(최소 공통 조상, Lowest Common Ancestor)
  
  

💻 Java code

import java.io.*;
import java.util.*;

public class Main {
    static int N,M,K=0;

    // LCA 변수
    static int[] depth;
    static int[][] parent; // parent[K][V] : 정점 V의 2^k번째 조상정점 번호

    static ArrayList[] tree;

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        StringBuilder sb = new StringBuilder();

        // 1. 입력 & 초기화
        N = Integer.parseInt(br.readLine());

        // 2^K > N인 K찾기
        for(int i=1; i<=N; i*=2)
            K++;

        // LCA 초기화
        depth = new int[N+1];
        parent = new int[K][N+1];

        // TREE
        tree = new ArrayList[N+1];
        for(int i=1; i<=N; i++)
            tree[i] = new ArrayList<Integer>();

        for(int i=1; i<N; i++) {
            st = new StringTokenizer(br.readLine());
            int v1 = Integer.parseInt(st.nextToken());
            int v2 = Integer.parseInt(st.nextToken());

            // 양방향 간선
            tree[v1].add(v2);
            tree[v2].add(v1);
        }

        // 2. DETPH 확인
        dfs(1,1);

        // 3. 2^N까지 parent 채우기
        fillParent();

        // LCA 진행
        M = Integer.parseInt(br.readLine());
        for(int i=0; i<M; i++) {
            st = new StringTokenizer(br.readLine());
            int v1 = Integer.parseInt(st.nextToken());
            int v2 = Integer.parseInt(st.nextToken());

            // 공통 조상 출력
            sb.append(LCA(v1, v2)+"\n");
        }

        System.out.println(sb);
    }

    // 최소 공통 조상
    private static int LCA(int a, int b) {
        // 1. depth[a] >= depth[b]이도록 조정하기
        if(depth[a] < depth[b]) {
            int tmp = a;
            a = b;
            b = tmp;
        }

        // 2. 더 깊은 a를 2^K승 점프하여 depth 맞추기
        for(int i=K-1; i>=0 ; i--) {
            if(Math.pow(2, i) <= depth[a]-depth[b])
                a = parent[i][a];
        }

        // 3. depth를 맞췄는데 같다면 종료
        if(a==b)
            return a;

        // 4. a-b는 같은 depth이므로 2^K승 점프하며 공통부모 바로 아래까지 올리기
        for(int i=K-1; i>=0; i--) {
            if(parent[i][a] != parent[i][b]) {
                a = parent[i][a];
                b = parent[i][b];
            }
        }

        return parent[0][a];
    }

    // 부모 채우기
    private static void fillParent() {
        for(int i=1; i<K; i++) {
            for(int j=1; j<=N; j++) {  // 1~N번까지 정점 번호
                // 정점 N의 2^K번째 조상 정점 번호
                parent[i][j] = parent[i-1][parent[i-1][j]];
            }
        }
    }

    // DEPTH 확인 DFS
    static void dfs(int id, int cnt) {
        // 1. depth 기록
        depth[id] = cnt;

        // 2. 자식들의 depth 기록
        for(int i=0; i<tree[id].size(); i++) {
            int next = (Integer)tree[id].get(i);
            if(depth[next] == 0) {
                dfs(next, cnt+1);
                parent[0][next] = id;  // 바로 위(1번째 부모를 기록)
            }
        }
    }
}