[백준] 2957번 이진 탐색 트리

🔔 문제

https://www.acmicpc.net/problem/2957

🎯 풀이방법

이진 탐색 트리의 삽입의 성질을 제대로 이해해야 풀 수 있는 문제이다. 만약 제시된 pseudo code대로 문제를 푼다면 시간초과가 발생한다. 왜냐하면 최악의 경우 30만개가 1부터 30만까지 차례대로 들어온다면 시간복잡도는 O(N^2)이다.

이 문제에서는 카운터 C만 출력하면 된다. C는 이진트리에 삽입이 될 때 누적된 높이의 값이다. 이를 풀기 위해서는 이진 탐색 트리에서 삽입할 때의 특징을 찾아야 한다. 만약 x라는 값을 삽입한다면, x는 x보다 작은 값들 중 가장 큰 값의 오른쪽에 삽입 또는 x보다 큰 값들 중 가장 작은 값의 왼쪽에 삽입된다. 예를 들어, 트리에 3과 5가 삽입된 상태에서 4를 삽입된다면 어떻게 될까?
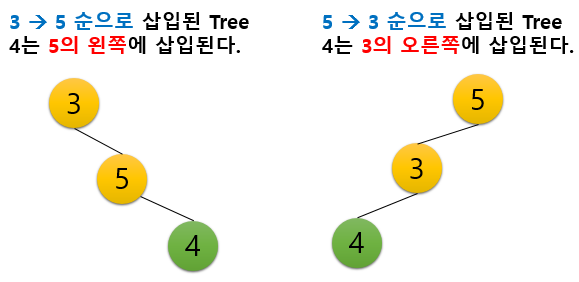위의 2가지 경우로 나뉘게 된다. 결과적으로 어느쪽에 삽입되는 가를 결정하는 것은 누가 먼저 삽입되었는가에 달려있고 이는 높이가 더 깊은 쪽에 삽입된다라고 말할 수 있다. 이를 일반화하면, x의 값보다 작은 것들 중 가장 큰 것의 높이와 x의 값보다 큰 것들 중 가장 작은 것의 높이를 비교한 후, 높이가 더 깊은 것에 +1을 한 것이 x의 높이가 된다.

depth[num] = Math.max(depth[treeSet.lower(num)], depth[treeSet.higher(num)]) + 1;

✔ Java의 TreeSet

이진 탐색 트리 구조로 데이터를 저장하는 클래스이다. TreeSet은 BST 중에서도 성능을 향상시킨 레드-블랙 트리로 구현되어 있기 때문에 부모노드보다 작은 값을 가지는 노드는 왼쪽 자식으로, 큰 값을 가지는 노드는 오른쪽 자식으로 배치하여 데이터의 추가나 삭제 시 트리가 한쪽으로 치우쳐지지 않도록 균형을 맞추어준다.

lower과 higher 메소드
lower 메소드는 해당 객체 바로 아래에 있는 객체를 찾아준다. higher은 해당 객체 바로 위에 있는 객체를 찾아준다. 주의할 점은 x보다 큰 값이 없거나 작은 값이 없을 경우 null을 리턴해주므로 이에 대한 예외처리를 해줘야 한다.

TreeSet<Integer> treeSet = new TreeSet<Integer>();
treeSet.add(new Integer(90));
treeSet.add(new Integer(35));
treeSet.add(new Integer(75));
treeSet.add(new Integer(100));
treeSet.add(new Integer(100));

System.out.println(treeSet.lower(100));  // 90 출력
System.out.println(treeSet.higher(75));  // 90 출력

💡 이 문제에서 얻어갈 것

BST의 특징에 대해 정확히 이해해야 이 문제를 풀 수 있다. 단순히 BST 구현만 한다면 시간초과로 풀 수 없다.

💻 java code

import java.io.*;
import java.util.*;

public class Main {
    static int N;
    static long count=0;
    static int depth[];

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();

        N = Integer.parseInt(br.readLine());
        depth = new int[N+2];

        // 초기화
        // TreeSet : 이진탐색트리, 작은 값은 왼쪽 자식으로, 큰 값은 오른쪽 자식으로
        TreeSet<Integer> treeSet = new TreeSet<>();
        treeSet.add(0);
        treeSet.add(N+1);

        depth[0] = -1;
        depth[N+1] = -1;

        for(int i=0; i<N; i++) {
            int num = Integer.parseInt(br.readLine());

            // lower : 해당 객체 바로 아래에 있는 객체, higher : 바로 위에 있는 객체
            // 깊이가 더 깊은 수를 선택해 그 밑에 위치
            depth[num] = Math.max(depth[treeSet.lower(num)], depth[treeSet.higher(num)]) + 1;
            treeSet.add(num);

            // count update
            count += depth[num];
            sb.append(count + "\n");
        }

        System.out.println(sb);
    }
}

시간 초과 코드

import java.io.*;
import java.util.*;

public class Main {
    static class Node {
        int num;
        Node left, right;

        public Node(int num) {
            this.num = num;
        }
    }

    static int N, count=0;

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();

        //  입력
        N = Integer.parseInt(br.readLine());

        // root Node 입력
        int rootNum = Integer.parseInt(br.readLine());
        Node root = new Node(rootNum);
        sb.append(count + "\n");
        
        if(N <= 1) {
            System.out.println(sb);
            return;
        }

        // 2~N까지 입력
        for(int i=2; i<=N; i++) {
            int x = Integer.parseInt(br.readLine());
            insert(x, root);
            sb.append(count + "\n");
        }

        System.out.println(sb);
    }

    public static void insert(int x, Node node) {
        count++;

        if(x<node.num) {
            if(node.left == null)
                node.left = new Node(x);
            else
                insert(x, node.left);
        } else {
            if(node.right == null)
                node.right = new Node(x);
            else
                insert(x, node.right);
        }
    }
}