
🔔 문제
https://www.acmicpc.net/problem/2579
🎯 풀이방법
계단을 오르는데 3가지 제한 조건이 있다.
1) 계단은 한 번에 1칸 또는 2칸씩 오를 수 있다
2) 연속된 3개의 계단을 밟으면 안된다. 즉, 전전계단을 밟을 수 없다
3) 마지막 도착 계단은 반드시 밟는다.dp[i] : i번째 계단에서 얻을 수 있는 최대 점수로 정의한다면, 다음과 같은 점화식을 얻을 수 있다.
dp[i] = Math.max(steps[i]+p[i-2], steps[i]+steps[i-1]+dp[i-3])
해석하자면, 현재 계단에서 2칸 점프로 온 경우 또는 1칸 점프로 온 경우 중 최댓값을 선택한다.
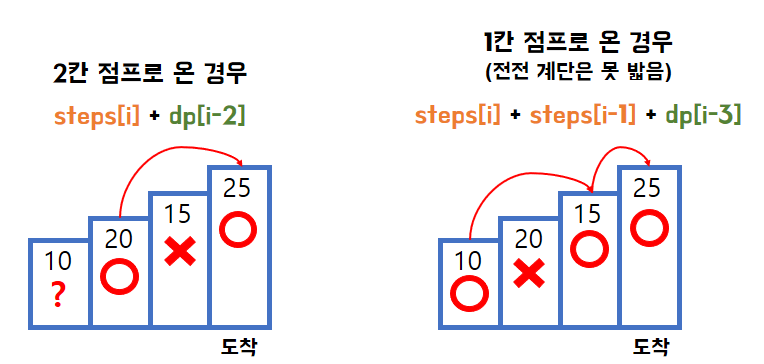
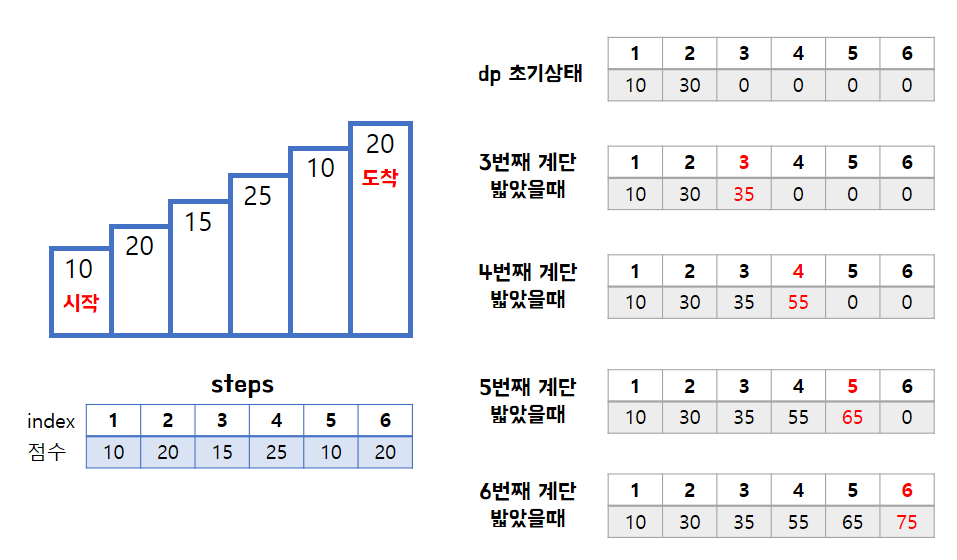
그렇다면 1번째 예제에서 위의 점화식으로 계산한다면 아래의 그림으로 표현할 수 있다.
💡 이 문제를 통해 얻어갈 것
다이내믹 프로그래밍(DP) 사고방식으로 생각하기
📝 java code
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class bj_2579 {
static int N;
static int[] steps, dp;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
steps = new int[N+1];
dp = new int[N+1];
for(int i=1; i<=N; i++)
steps[i] = Integer.parseInt(br.readLine());
// 1. 1칸 : 밟은게 최댓값, N==1이면 종료
dp[1] = steps[1];
if(N<=1) {
System.out.println(dp[1]);
return;
}
// 2. 2칸 : 1칸+2칸 연달아 밟기가 최대
dp[2] = steps[1] + steps[2];
// 3. 3칸 ~ N칸 : DP 진행
for(int i=3; i<=N; i++) {
// 현재 계단 점수 + 2칸 점프 vs 1칸 점프 (연달아 온 거 제외)
dp[i] = Math.max(steps[i]+dp[i-2], steps[i]+steps[i-1]+dp[i-3]);
}
System.out.println(dp[N]);
}
}