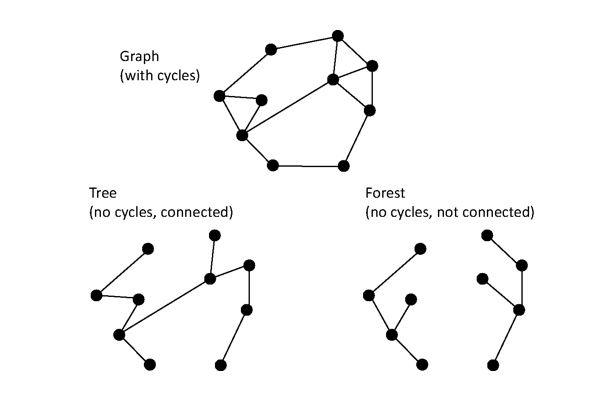
✔ 그래프(Graph)
- 현실세계의 사물이나 개념 간의 연결 관계를 수학적 모델로 단순화하여 표현한 것
- 정점(vertex)과 정점 간의 연결 관계를 나타내는 간선(edge)으로 이루어진 자료구조
| 종류 | 의미 |
|---|---|
Undirected Graph | 무향 간선(=방향이 없는 간선)으로 이루어진 그래프 |
Directed Graph | 유향 간선(=방향이 있는 간선)으로 이루어진 그래프 |
가중치 그래프 | 가중치를 갖는 간선으로 이루어진 그래프 |
Connected Graph | 임의의 두 정점 v1,v2에 대해서 경로 Path(v1,v2)가 존재하는 그래프 |
부분 그래프 | 어떤 그래프의 정점 집합의 부분집합과 그에 속한 간선들로 이루어진 그래프 어떤 그래프의 간선집합의 부분집합과 그에 속한 정점들로 이루어진 그래프 |
트리 그래프 | 순환을 갖지 않는 연결 그래프 임의의 두 정점에 대하여 경로가 정확히 1개 존재한다 |
서로소 집합(Union-Find)
-
교집합이 공집합인 집합(서로소 집합)들의 정보를 확인(Find)하고 조작(Union)할 수 있는 자료구조
-
Union 연산
- 어떤 두 원소 a,b에 대해서 union(a,b)는 각 원소가 속한 집합을 하나로 합치는 연산
- 하나의 루트 노드를 다른 하나의 루트노드의 자식노드로 넣어 두 트리를 합침
def union(a,b):
A_root = find(a)
B_root = find(b)
parent[A_root] = B_root- Find 연산
- 어떤 원소 a에 대하서 a가 속한 집합을 반환
- 주어진 원소의 루트 노드 번호를 반환
def find(a):
if(parent[a]==a)
return a
else return parent[a] = find(parent[a])✔ 트리 (Tree)
- 자료들 사이의 계층적 관계를 나타내는데 사용하는 자료구조로 부모-자식 관계로 표현된다
- Connected Acyclic Graph의 한 종류이다
- 루트 노드가 존재한다.
- 트리의 부분트리 또한 트리 구조이다.
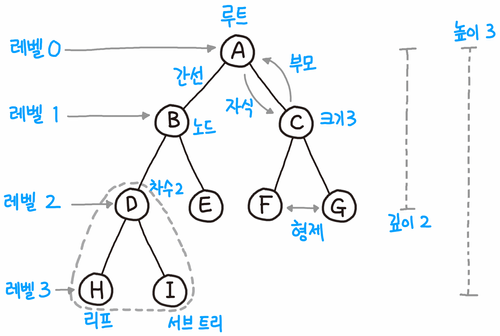
| 용어 | 의미 |
|---|---|
루트 노드 (Root Node) | 트리의 최상위 노드 |
깊이 (Depth) | 루트 노드에서 해당 노드까지 도달하는데 사용하는 간선의 갯수 |
레벨 (Level) | 깊이 + 1 |
트리의 분지 수 | 해당 트리 내 모든 노드의 분지 수 중 최댓값 |
내부 노드 (internal Node) | 자식이 있는 노드 |
외부 노드 (leaf Node) | 자식이 없는 노드 |
높이 (Height) | 루트 노드에서 해당 노드까지 도달하는데 지나간 정점의 갯수 |
이진 트리
: 트리의 분지 수가 2 이하인 트리
- 자식이 최대 2개이므로 왼쪽 자식과 오른쪽 자식으로 구분한다.
- 높이가 N인 이진 트리의 최대 노드 개수는 2^N-1개이다.
| 종류 | 의미 |
|---|---|
정 이진 트리 (Full Binary Tree) | 모든 노드의 차수가 0 or 2인 이진 트리 |
포화 이진 트리 (Perfect Binary Tree) | 정 이진 트리에서 모든 단말 노드의 깊이가 같은 이진 트리. 높이가 H인 포화 이진 트리의 노드 개수는 2^H-1개이다. |
완전 이진 트리 (Complete Binary Tree) | 마지막 레벨은 노드가 왼쪽에 몰려있고 마지막 레벨을 제외하면 포화 이진 트리 구조를 띄고 있는 이진 트리 |
사향 이진 트리 (Skewed Binary Tree) | 연결리스트처럼 한 줄로 연결 되어 있는 형태의 이진 트리 |
이진 트리의 순회
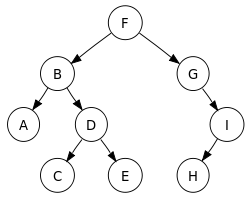
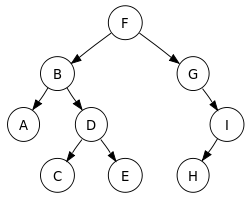
이진 트리의 순회는 왼쪽 자식 탐색, 오른쪽 자식 탐색, 현재 노드 방문의 3가지 주요 과정을 통해 진행되며, 노드 방문 순서에 따라 전위 순회(pre-order), 중위 순회(in-order), 후위 순회(post-order)로 나뉜다.
- 전위 순회 : ROOT → LEFT → RIGHT (FBADCEGIH)
- 중위 순회 : LEFT → ROOT → RIGHT (ABCDEFGHI)
- 후위 순회 : LEFT → RIGHT → ROOT (ACEDBHIGF)
힙 (Heap)
: 완전 이진트리 형태의 자료구조. 일반적으로 그룹을 정렬하거나 입력된 데이터 안에서 최소/최대 값을 찾을 때 사용한다. 데이터의 삽입과 삭제가 빠르며 각각의 수행시간이 O(logN)이다.
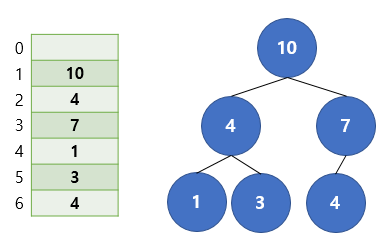
- 최소 힙 (Min Heap) : 부모 노드의 키 < 자식 노드의 키
- 최대 힙 (Max Heap) : 부모 노드의 키 > 자식 노드의 키
▶ 힙의 삽입 연산
1. 트리의 가장 마지막 위치에 노드를 삽입한다.
2. 추가된 노드와 그 부모의 노드가 힙 조건을 만족하는지 확인한다
3. 만족하지 않는다면 부모와 자식의 키 값을 바꾼다.
4. 조건에 만족하거나 추가된 노드가 루트에 도달할 때까지 2~3 과정을 반복한다.
▶ 힙의 삭제 연산
1. 루트 노드를 삭제한다
2. 트리의 가장 마지막 노드를 루트 자리로 삽입한다
3. 바꾼 위치의 노드가 힙 조건을 만족하는지 확인한다
4. 만족하지 않는다면 왼쪽 자식과 오른쪽 자식 중 적합한 노드와 키 값을 바꾼다.
5. 조건을 만족하거나 리프 노드에 도달할 때까지 3~4 과정을 반복한다.
📌 요약
그래프
1) 2개 이상의 경로가 가능하다. 노드들 사이에 무방향/방향에서 양방향 경로를 가질 수 있다.
2) self-loop 뿐 아니라 loop/circuit 모두 가능하다.
3) 루트 노드라는 개념이 없다.
4) 부모-자식 관계라는 개념이 없다.
5) 그래프의 순회는 DFS나 BFS로 이루어진다.
6) 그래프는 Cyclic 혹은 Acyclic이다.
7) 그래프는 크게 방향 그래프와 무방향 그래프가 있다.
8) 간선의 유무는 그래프에 따라 다르다.
9) 그래프는 네트워크 모델이다.
트리
1) 트리는 그래프의 특별한 케이스이며 "최소 연결 트리"라고도 불린다. 두 개의 정점 사이에 반드시 1개의 경로만을 가진다.
2) loop나 circuit이 없다. 당연히 self-loop도 없다.
3) 한 개의 루트 노드만이 존재하며 모든 자식노드는 한 개의 부모노드만을 가진다.
4) 부모-자식 관계이므로 흐름은 top-bottom 아니면 bottom-top으로 이루어진다.
5) 트리의 순회는 Pre-order, In-order 아니면 Post-order로 이루어진다. 이 3가지 모두 DFS/BFS안에 있다.
6) 트리는 DAG(Directed Acyclic Graphs)의 한 종류이다. DAG는 사이클이 없는 방향 그래프를 말한다.
7) 트리는 이진트리, 이진탐색트리, AVL 트리, 힙이 있다.
8) 간선은 항상 정점의개수-1 만큼을 가진다.
9) 트리는 계층 모델이다.
백준 추천 문제
jeewoo1025.velog의 백준 문제 추천에서 "그래프" 문제들
🔔 QUIZ
- 트리의 정의에 대해 설명하세요
- 최소신장트리란? 최소신장트리를 구하기 위한 알고리즘 2가지를 설명하시오.
- 트리의 높이를 구하는 알고리즘을 재귀적으로 구성해보시오.
- tree traversal의 3가지 방식을 설명하시오.
- 그래프의 정의는? 트리와 그래프의 관계는?
- 트리와 숲의 차이는?
- 이진트리의 높이가 logN이 이유는?
👩🏫 답
1. 트리는 DAG(사이클이 없는 방향 그래프)의 일종으로 부모-자식 같은 계층적 관계를 나타내는 데 사용하는 자료구조이다. 루트 노드가 존재하고 트리의 부분트리 또한 트리 구조이다.
2. 최소신장트리(Minimum Spanning Tree, MST)는 Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리이다. Spanning Tree는 그래프에서 일부 간선을 선택해서 만든 트리를 말한다. Spanning Tree의 특징은 모든 정점들이 연결되어 있어야 하고 사이클을 포함해서는 안된다.
- 크루스칼 알고리즘 : Greedy method를 이용하여 그래프의 모든 정점을 최소 비용으로 연결하는 최적의 해를 구하는 것. O(elog₂e)
- 프림 알고리즘 : 시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장해나가는 방법. O(n^2)
3. 트리의 높이와 너비 문제 참고
- 중위 순회(in-order) DFS 알고리즘을 적용
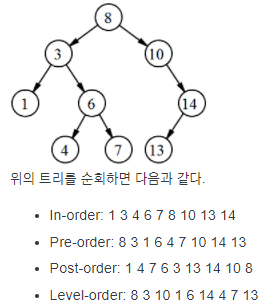
4. 트리 순회는 노드의 방문 순서에 따라 전위 순회(pre-order), 중위 순회(in-order), 후위 순회(post-order)로 나눌 수 있으며 추가적으로 레벨 순서 순회가 있다.
- 전위 순회 : 현재노드 → 왼쪽 노드 → 오른쪽 노드 순서로 방문
- 중위 순회 : 왼쪽노드 → 현재노드 → 오른쪽 노드 순서로 방문
- 후위 순회 : 왼쪽노드 → 오른쪽 노드 → 현재노드 순서로 방문
- 레벨 순서 순회 : 너비 우선 순회라고도 하며, 노드를 레벨 순서로 방문하는 순회 방법.
5. 그래프는 현실 세계의 사물이나 개념 간의 연결 관계를 수학적 모델로 단순화하여 표현한 것으로 정점(vertex)와 정점을 연결하는 간선(edge)으로 이루어진 자료구조이다.

6. 포레스트(Forest)는 하나 이상의 트리로 이루어진 집합이다. n개의 서브 트리를 가진 루트 노드를 제거하면, n개의 분리된 트리가 생겨 포레스트를 이룬다.
7. 처음에 1개, 그 다음 세대의 자식이 2개, 그 다음 세대의 자식이 4개, ... 즉, 이진 트리는 1개로부터 2개씩 되는 모양이다. 전체 노드의 개수에 따른 높이를 살펴보면
전체 노드의 개수가 1개일 때 0
전체 노드의 개수가 2개일 때 1
전체 노드의 개수가 3개일 때 1
전체 노드의 개수가 4개일 때 2
전체 노드의 개수가 5개일 때 2
전체 노드의 개수가 6개일 때 2
전체 노드의 개수가 7개일 때 2
전체 노드의 개수가 8개일 때 3
...
위의 규칙을 바탕으로 전체 노드의 개수가 n이라고 했을 때 높이는 logN이다.
