기사단원의 무기 (자바)

김재현·2023년 11월 27일

알고리즘 풀이

목록 보기

30/90

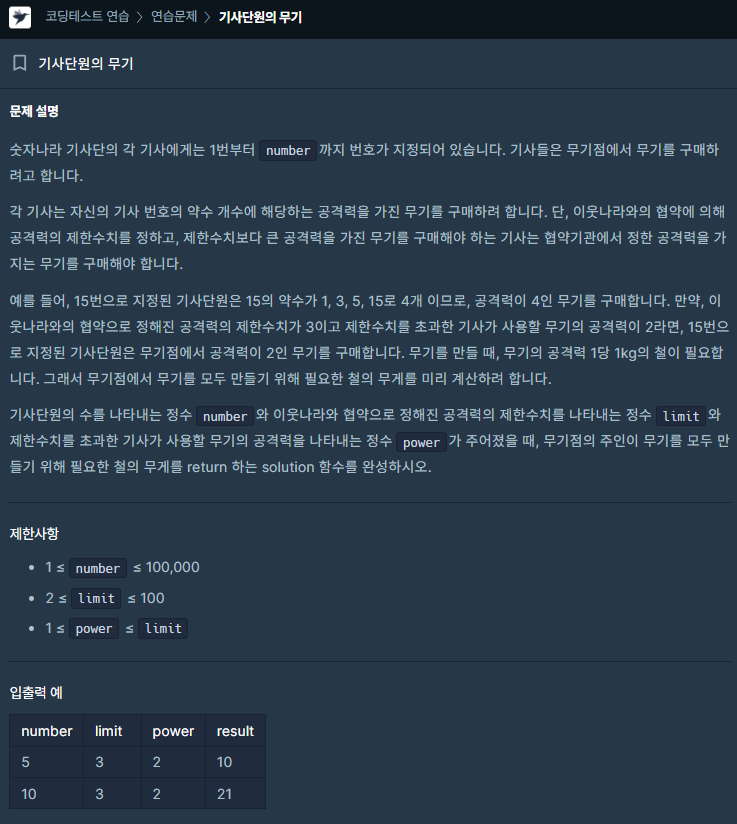
문제

정답 코드

class Solution {
    public int solution(int number, int limit, int power) {
        int answer = 0;
        
        int[] powerArray = new int[number];
        
        // 처음의 약수 구하는 코드 -> 시간초과
//        for(int i=0;i<number;i++) {
//            for(int j=1;j<=i+1;j++) {
//                if ((i+1) % j == 0) {
//                    powerArray[i]++;
//                }
//            }
//        }

        for(int i=0;i<number;i++) {
            for(int j=1;j*j<=i+1;j++) {
                if(j*j==i+1) {
                    powerArray[i]++;
                } else if ((i+1) % j == 0) {
                    powerArray[i]+=2;
                }
            }
        }

        for(int i=0;i<number;i++) {
            if (powerArray[i]>limit) {
                powerArray[i]=power;
            }
            answer+=powerArray[i];
        }
        
        return answer;
    }
}

약수 구한 뒤 그 숫자를 비교하여 limit으로 맞추고 count하는 문제였다.
쉽게 풀었지만 시간 초과가 떴다..!!

어떻게 줄여야하나 고민하다가 저번주에 포스팅했던 제곱근이 생각났다.
그때는 소수 판별을 위해 썼는데, 약수를 구할 때도 같은 방식으로 구할 수 있겠다고 생각했다.
그리고 성공!
(for문을 i=0으로 시작해서 복잡해보인다. 차라리 i=1로 시작하고 powerArray[i-1]로 할 껄 그랬다.)

다른 사람 풀이

class Solution {

    public int solution(int number, int limit, int power) {
        int[] count = new int[number + 1];    
        for (int i = 1; i <= number; i++) {
            for (int j = 1; j <= number / i; j++) {
                count[i * j]++;
            }
        }
        int answer = 0;
        for (int i = 1; i <= number; i++) {
            if (count[i] > limit) {
                answer += power;
            } else {
                answer += count[i];
            }
        }
        return answer;
    }
}

약수의 개수를 이렇게도 구할 수 있겠구나!

i의 배수들을 찾아가며 해당 위치의 배열 값을 증가.
예를 들어, i가 2이면 2, 4, 6, 8, ... 등의 위치의 배열 값을 1씩 증가.

하고 돌려봤는데 나보다 빠르다!?

시간복잡도

왜 내것이 더 느리지 궁금해서 시간복잡도를 구해보았다.

여기서 잠깐, 시간복잡도란? (ㅋㅋㅋ)
시간 복잡도는 알고리즘이 문제를 해결하는 데 걸리는 시간의 증가율을 나타내는 개념이다.
일반적으로 입력 크기에 대한 함수로 표현되며 알고리즘의 효율성을 평가한다.
입력이 커질수록 알고리즘의 성능이 어떻게 변하는지를 설명한다.

시간 복잡도는 일반적으로 "O 표기법"으로 나타내어지며, 입력 크기에 대한 함수를 나타낸다.
("O"는 "Order of"의 약자로, 주어진 함수의 상한을 나타낸다.)

내가 풀이한 시간 복잡도는 제곱근을 이용했기 때문에 -> O(number * sqrt(number))
다른 사람의 시간 복잡도는 for문을 2번 돌리는 것이기 때문에 -> O(number^2)