문제

"Tiling" 알고리즘 문제를 풀어봤다.

문제는 다음과 같다.

• 세로가 2의 크기를 갖는 공간에 타일들을 깔아 넣는 작업을 하려고 한다.
• 타일 하나는 1*2의 크기를 갖는다.
• 가로가 n의 정수로 주어질 때, 똑같이 생긴 타일들로 주어진 공간을 채워넣는 경우의 수는 몇이 될까?

그림으로 보면 더 이해하기 쉬울 것 같다.

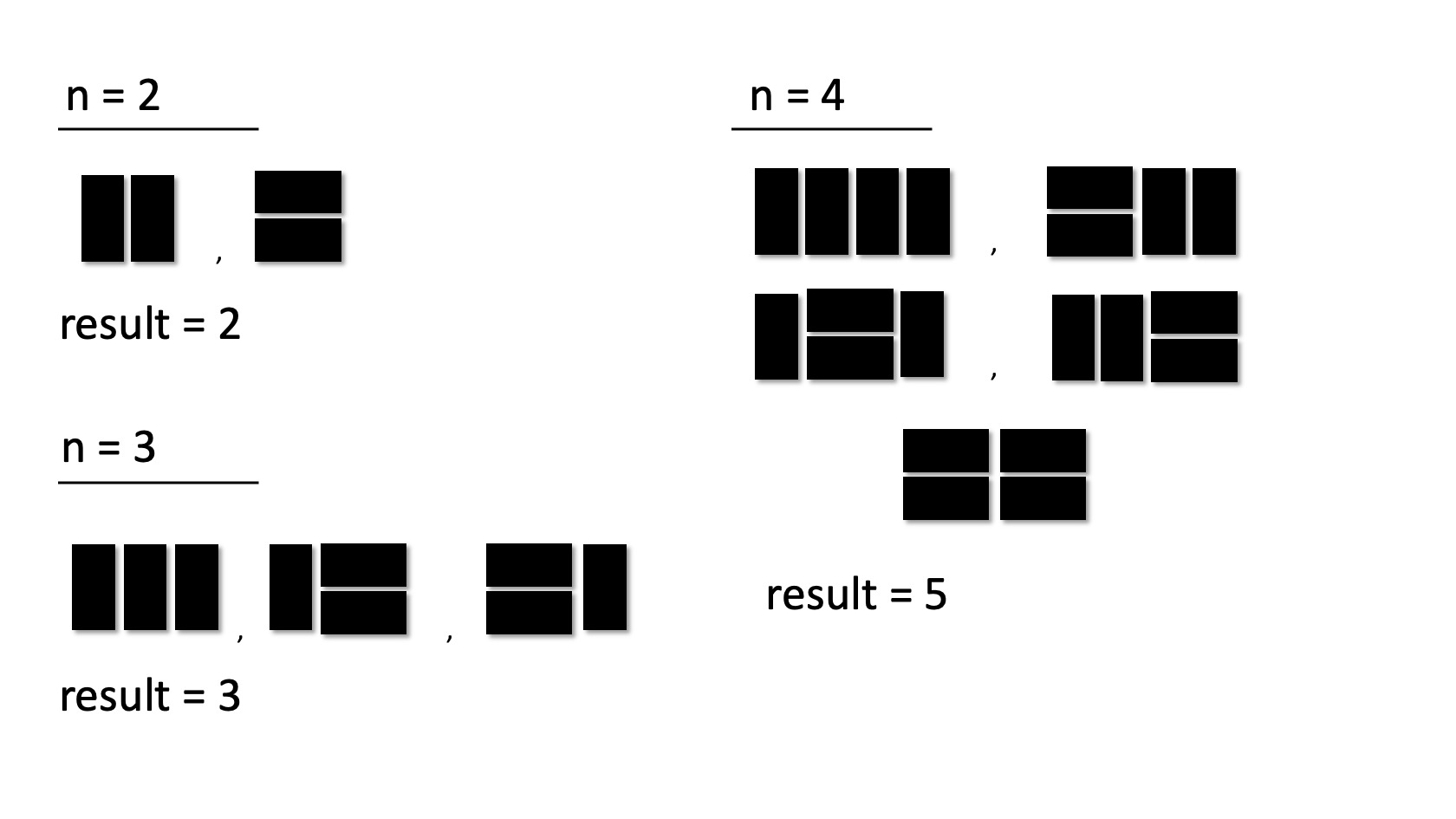
접근방법

우선 나는 규칙을 찾아보려고 했다. 신경써야할 사항들이 많았다. 타일 하나가 가로로 놓인다면 나머지 한 타일도 가로로 놓여야 한다. 그리고 가로로 놓일 수 공간이 생기는 만큼 경우의 수도 증가했다.
n에 대한 방적식이 있을지 고민해봤다. 나는 조합으로 생각해봤다. 가로로 놓인 타일은 한 묶음으로 생각하고 n*2의 공간에 가로로 놓일 수 있는 공간이 몇일지 나눠봤다.
만약 n이 5으로 주어지면 가로로 놓일 수 있는 공간은 최대 2 공간이 나오고, 1공간 그리고 아예 가로로 놓이지 않은 경우가 생긴다. 그리고 각각의 경우 남은 곳은 세로의 타일이 어떻게 매워지는지에 따라서 경우의 수가 늘어난다.

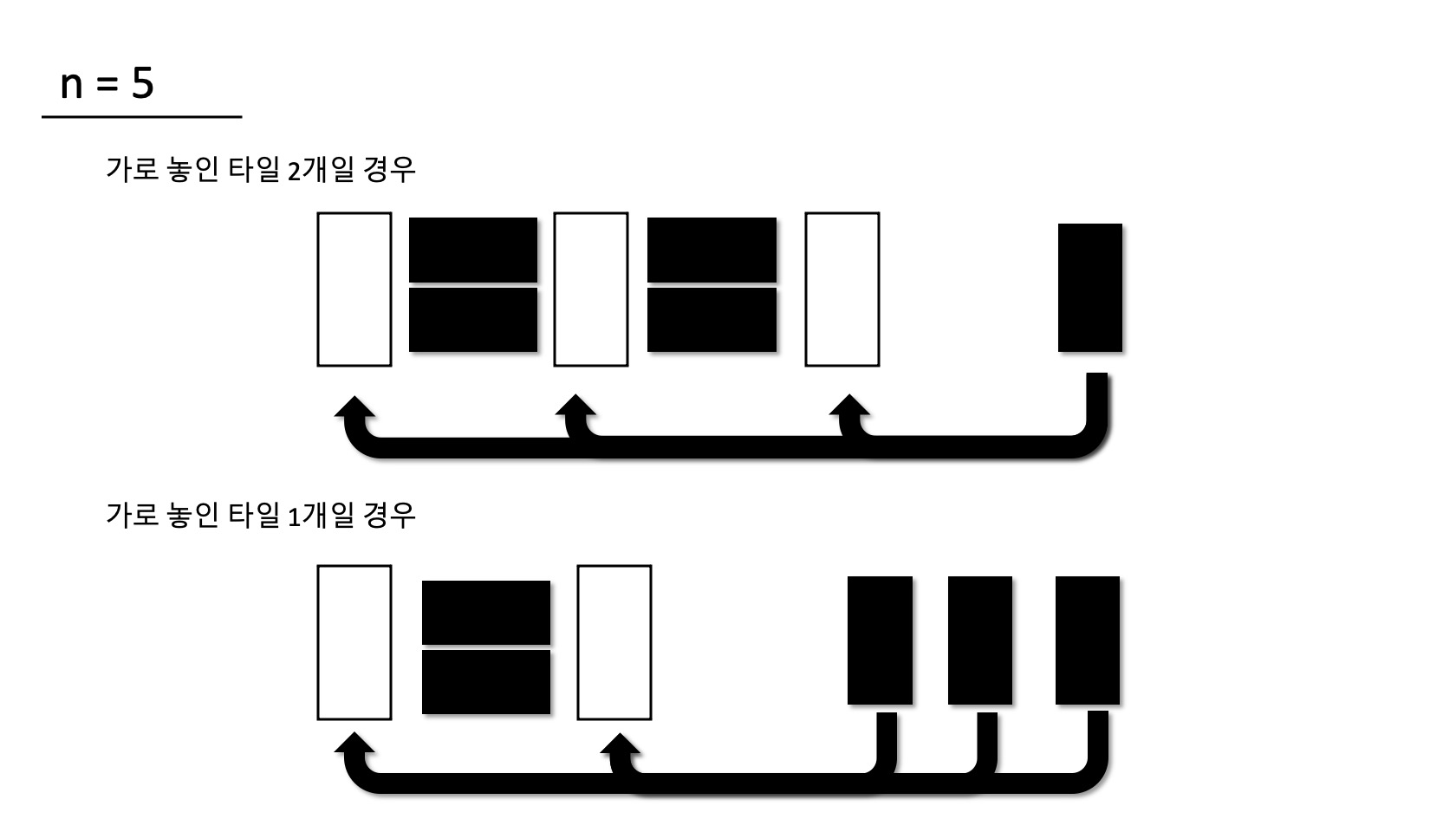
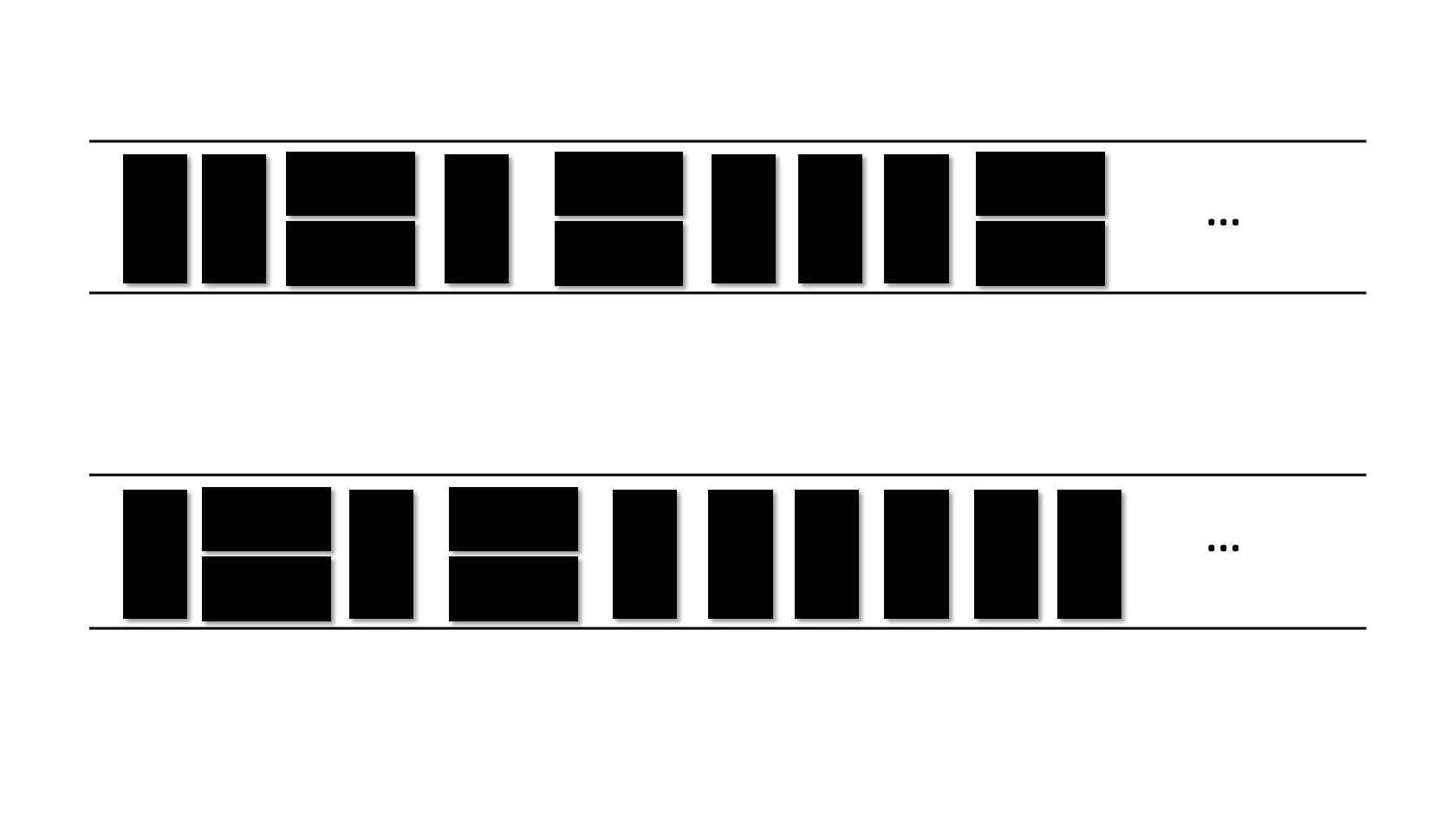
여기까지 생각이 미친 순간 나는 조합을 생각했다. 가로로 놓이는 타일들 사이사이에 몇 개의 남은 세로 타일이 들어가는 지를 따지고 모든 경우의 수를 더하면 답이 나온다. 가로로 놓인 타일이 파티션이 되는 것이다.
중복조합이다

중복조합으로 다음과 같이 경우의 수를 구하고보니, 규칙이 또 보였다. 피보나치였다.
결국 이 문제는 n의 경우를 구하려면 n-1의 경우의 수와 n-2의 경우의 수를 더하여 구하면 되는 간단한 문제였다.

풀이

let tiling = function (n) {
  let memo = []

  memo[0] = 0 ; memo[1] = 1; memo[2] = 1; memo[3] = 2;

  let k = n + 1

  function takeSum(k, memo){
    if (memo[k] !== undefined) return memo[k];

    memo[k] = takeSum(k-1, memo) + takeSum(k-2, memo);
    
    return memo[k]
  }
  return takeSum(k, memo);
};

예전에 만들어놨던 피보나치 코드를 약간만 수정해서 제출했다. 코드 자체는 개선해야될 게 많다. 하지만 나는 그 이전에 다른 문제를 고민해봤다. 자바스크립트를 기반으로 했다.

고민

또 재귀 문제를 눈 앞에서 놓쳤다. 아직도 추상화가 안된다. 어떻게 문제를 보고 재귀를 써야하는 문제라는 것을 판단할 수 있을까?
정답을 제출하고 해설을 보면 이렇게 나온다.

이때, 타일이 아직 놓이지 않은 부분은 사실 크기만 다를뿐 같은 종류의 문제라는 것을 알 수 있다.

하지만 나는 앞으로도 같을 거라는 것을 확신하지 못했다. 그리고 왜 n-1의 경우 생기는 모양의 개수와 n-2의 경우 생기는 모양의 개수를 더한 게 n의 경우의 모양들을 형성하는 지 의미를 찾아내지 못했다. 나는 이 문제가 위 해설처럼 쉽게 풀리는 문제가 절대 아니라고 믿는다.

참고

• 보물 고블린의 보물창고 <- 정말 개념을 잘 정리해놓고 있는 사이트 강추