[알고리즘] 피보나치 재귀 구현으로 배운 메모이제이션(Memoization)

피보나치 수열은 학교 수학 시간에 수열을 배울 때 잠깐 구경했었다.
피보나치 수열은 어떤 수열의 n번째 항목이 n-1번째 항목과 n-2번째 항목의 합과 같다.
수식으로 정리하자면 다음과 같다.

$P_n = P_{n-1} + P_{n-2}$

이번에 구현하는 피보나치 수열의 조건은 다음과 같다.

$P_0=0$, $P_1=1$, $P_n$ 을 구하여라
단 for, while을 사용하지 말 것.

처음 구현한 피보나치 재귀 함수

function fibonacci(num) {
  // 종료조건문
  if (num === 0) return 0;
  else if (num === 1) return 1;
  
  return fibonacci(num-1) + fibonacci(num-2);
}

작은 수에서는 잘 작동하는 모습을 보인다. 하지만 구하고자 하는 항목 n의 크기가 커질수록 연산도 기하급수적으로 늘어난다. 이는 한 피보나치 함수가 두 개의 피보나치 호출하기 때문이다. 위 피보나치 재귀 함수의 시간 복잡도는 그래서 $O(n^2)$이다. 어떻게 하면 효율이 더 좋은 함수를 만들 수 있을까?

메모이제이션(Memoization)

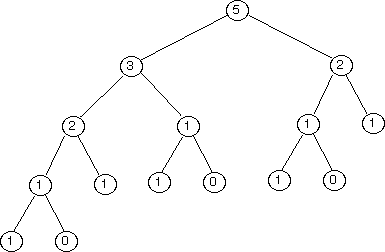
피보나치 수열을 트리구조로 살펴보면 위와 같은 그림이 되겠다. 위 그림에서 우리는 반복되는 서브 트리가 있다는 것을 확인할 수 있다. 위에서 구현한 재귀함수는 현재의 스택에서 반환값을 얻기 위해 다른 함수의 반환값을 계산해야 한다. 하지만 이미 계산된 값을 참조할 수 있으면 반환값을 기다리지 않고 그 값을 반환하기만 하면 된다. 미리 계산된 값을 저장하고 다음번 똑같은 조건을 계산하게 될 때 값을 참조하게 설계하는 기법이 Memoization이다.

다시 구현한 피보나치 재귀 함수

function fibonacci(n) {
  let memo = [0,1] // 계산값을 저장할 배열, 배열 초기화

  function subFunc(n, memo){
    // 종료식
    if (memo[n] !== undefined) return memo[n];
	// 재귀 호출
    memo[n] = subFunc(n-1, memo) + subFunc(n-2, memo);
   	
    return memo[n]
  }

  return subFunc(n, memo);
}

생각보다 간단하다. 먼저 호출되는 재귀함수는 가장 긴 줄기를 가지기 때문에 피보나치 계산값을 거의 구하게 된다. 그리고 다음에 호출되는 재귀함수는 먼저 호출되었던 재귀함수가 구한 값들을 memo 배열에서 참조하기만하고 값을 반환한다. 값이 이미 계산된 재귀함수를 호출할 필요가 없는 것이다. 메모이제이션을 통해서 피보나치 함수를 최적화하는 방법을 알아보았다.