블록체인의 처음 모습은 PoW합의 알고리즘을 이용한 분산원장 시스템, 비트코인이었다. 그리고 블록체인 생태계는 계속해서 문제들을 해결하면서 발전을 해나가고 있다.
결국 블록체인은 증명하는 것이 핵심이다. 내가 코인을 가지고 있는지 없는지는 내 디지털 서명으로 소비 가능한 코인이 풀에 남아있는지(비트코인의 예), 아니면 해당 네트워크 참여자들 모두에 기록되는 나의 계정 잔고(이더리움의 예)를 통해서 증명할 수 있다. 내가 당신한테 코인을 보냈는지, 내가 보낸 코인이 누구한테 갔는지도 트랜잭션과 블록의 기록을 통해서 증명할 수 있다.

하지만 증명은 행해질수록 나의 프라이버시를 노출하게 된다. 블록체인에 오랫동안 기록된 내 소비 패턴과 거래 당사자들을 통해서 나를 특정할 수 있게 된다. 온체인 데이터로 남는 기록에 의한 프라이버시 문제를 해결하기 위해 여러 해결방법들이 나오고 있고, 그 중 영지식증명에 관심이 모여지고 있다.

영지식증명(Zero-Knowledge proof)

⌞ 동굴 예시

[Computer Science Stack Exchange 이미지]

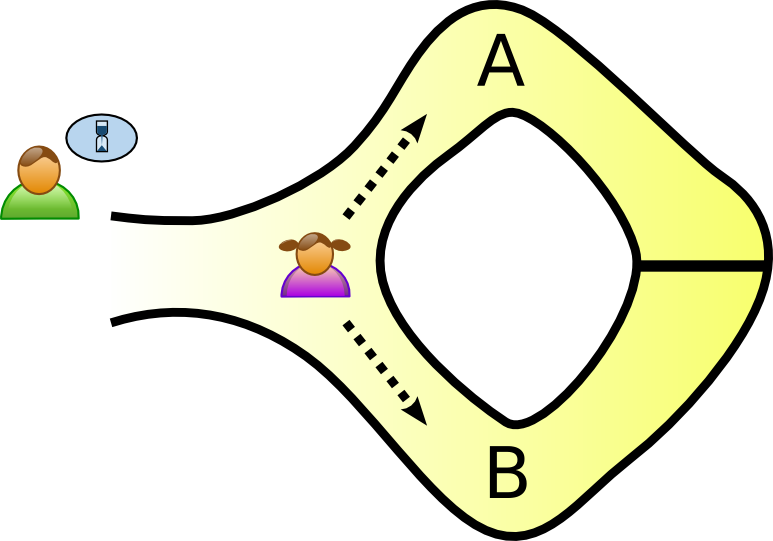
어린이용 영지식증명은 다음과 같다. 동굴은 한 통로로 들어가 다른 쪽 방향 통로로 나올 수 있는 구조이다. 하지만 중간에 자물쇠로 문이 잠겨져 있어 열쇠가 필요하다. 영희는 A와 B 어떤 방향으로든 동굴 안 깊숙히 들어간다.

이제 철수가 A와 B 통로를 모두 확인할 수 있는 동굴 입구로 와 영희에게 A 혹은 B 방향으로 나와보라고 한다. 철수가 말하는 통로로 영희가 매번 맞춰서 나온다면 우리가 추측해 볼 수 있는 사실이 무엇이 있을까? 물론 영희가 괴력을 발휘해 문을 부시고 나왔을 수도 있지만(그것도 능력이니까) 중간문 열쇠를 가지고 있다는 추론을 해볼 수 있다.

⌞ 수학적 구현

영지식 증명은 이산로그 문제를 기반으로 구현될 수 있다.
또한 갈루아체 라는 개념을 이해해볼 필요가 있는데, 갈루아체란 유한 개의 원소로 이루어진 체이다. 체는 우선 지금은 우리가 일반적으로 생각하는 연산들이 가능한 수들의 집합이라고 생각하면 되겠다.
갈루아는 체가 유한하기 위해서는 원소의 개수가 소수의 거듭제곱꼴이여야 한다고 밝힌다. $GF(p^n)$ 로 쓰인다.

유한체에서는 곱셈이 잘 정의된다는 특성을 가지고 있다고 한다. 이를 이산 거듭제곱이라고 한다.
아래 참고한 블로그에서는 다음의 예시를 들어 설명한다.

$Z_7$ 에서 3의 5 제곱을 생각했을 때, 그 값은 243이고. 7로 나눈 나머지는 5이다. $Z_7$에서 $3^5 = 5$이다.

이산 거듭제곱이 정의된다면 이산로그도 구해볼 수 있다.

$3^k ≡ 5(mod\ 7)$ 라고 수식을 쓸 수 있다면, 이를 만족하는 제일 작은 정수 k는 밑이 3인 5의 로그값이다.

암호학적으로는 유한체에서의 이산 거듭제곱은 쉽게 구할 수 있고, 유한체에서의 이산로그는 구하기가 어렵다는 점을 이용하여 암호체계를 만들 수 있다. 현재 예시는 비교적 쉽게 구해지지만 적당히 큰 p를 이용한다면 이산로그 계산의 난이도가 급격하게 커지고, 이는 거의 못 구할 정도라고 생각하면 된다.

이 문제를 증명 차원에서 사용을 하게 된다면 다음과 같이 사용할 수 있다.

$y=g\times x (mod\ p)$ 를 구하여 상대방에게 보낸다. 그리고 랜덤하게 구한 r 값으로 $C = g\times r(mod\ p)$를 구하여 또 상대방에게 보낸다. 상대방은 $(x+r)\ mod\ (p-1)$ 값이나 $r$값을 요구한다. 전자의 경우 $(C\times y)\ mod\ p ≡ g^{(x+r)\ mod\ (p-1)}\ mod\ p$ 로 $C \times y$를 검증할 수 있다. 후자의 경우는 $C≡g^r\ mod\ p$ 로 C를 검증할 수가 있다. $C\times y$ 와 $C$를 매 라운드마다 50% 확률로 검증을 해서 매번 y를 올바르게 계산을 해낼 수 있게 된다면 증명하는 사람이 확률적으로 y를 계산하기 위한 x를 알고 있다는 것을 충분히 받아들일 수 있다.

참고

• 브런치 블로그: 영지식 증명이란 무엇인가?
• soowon.log Velog: 이산 로그 문제