(javascript) 프로그래머스 배달

[링크]

https://programmers.co.kr/learn/courses/30/lessons/12978?language=javascript

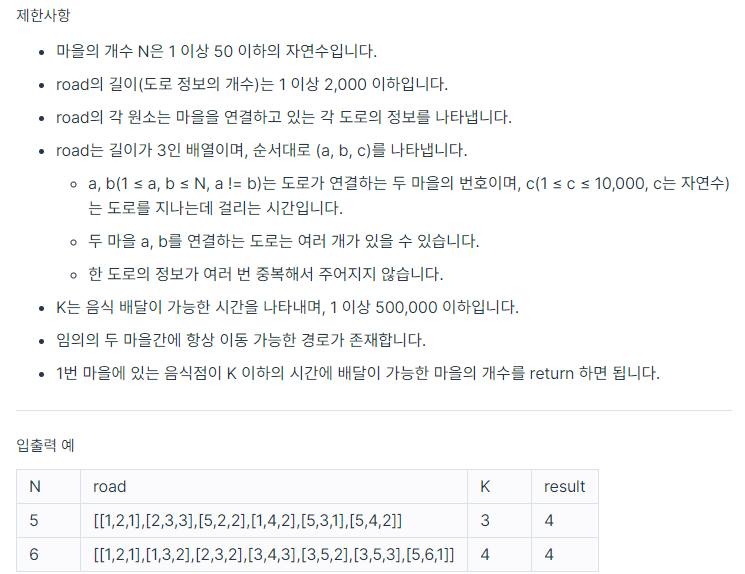
[문제]

[풀이]

처음에 문제를 보았을때 간선과 최소거리임을 확인하고 bfs로 풀이를 접근하였습니다. bfs에서는 queue에 visit하지 않은 node들을 넣고 FIFO해야하는데 이렇게 하려다 보니 최소거리가 갱신되지않거나, 같은 node를 계속해서 확인하는 경우가 생겼습니다.

다익스트라 알고리즘은 최단거리를 찾는 알고리즘인데, 이걸 적용하기 쉬운 문제였습니다. FIFO로만 queue를 추가하고 갱신하는 것은 최단거리를 얻지 못하는 경우가 생겼습니다. 하지만 다익스트라 알고리즘을 통해 현재 가보지않은 node들 중 edge가 최소인 것들을 가다보면 최단거리를 먼저 갱신할 수 있습니다.

다익스트라 알고리즘에서 제가 생각하는 중요한 핵심 코드는 이러합니다. 먼저 visited[]와 distance[] 배열을 만들어 visited==true 인 node들은 배열에 넣지않고 distance만 비교하여 다음에 확인할 node table을 갱신하는 것입니다.

[성공 코드]

// 전역변수
var limit
var distance = []
var visited = []
var result
function solution(N, road, K) {
  var answer = 0;
  
  //변수 초기화
  limit = K
  result = 0
  visited = new Array(N + 1).fill(false)
  /*10001 * N 인 이유는 간선의 최대값의 최대합 
  즉, 1~N까지 edge가 모두 10000이라면 distance는 10000*N이 될 수 있기 때문입니다*/
  distance = new Array(N + 1).fill(10001 * N)
  distance[1] = 0

  var pq = []

  pq.push(1)

  dijkstra(1, road, pq)
  return distance.filter((item) => { return item <= limit }).length;
}

function dijkstra(i, road, pq) {
  while (pq.length) {
    //splice는 배열을 return하기 때문에 pop()을 통해 꺼내 주었습니다.
    i = pq.splice(findMin(pq), 1).pop()
    if (visited[i]) continue
    visited[i] = true
    
    // road는 양방향 이기 때문에 item[0]과 item[1] 둘중 하나라도 존재하면 node에 붙은 edge입니다.
    var found = road.filter(item => { return item[0] == i || item[1] == i })
    found.sort((a, b) => a[2] - b[2])
    
    for (var item of found) {
      var src = i
      var dst = item[0] == i ? item[1] : item[0]
	  // 기존의 distance와 새로 찾은 distace의 비교 후 갱신
      if (distance[dst] > distance[src] + item[2]) {
        distance[dst] = distance[src] + item[2]
      }
      if (!visited[dst] && pq.indexOf(dst) == -1) {
        pq.push(dst)
      }

    }
  }
}

//이 함수는 arr중 ditance가 최소인 node의 arr index값을 리턴해 주는 함수 입니다.
function findMin(arr) {
  var min = distance[arr[0]]
  var idx = 0
  for (var i in arr) {
    if (min > distance[arr[i]]) {
      min = distance[arr[i]]
      idx = i
    }
  }
  return idx
}