Algorithm with Math - GCD / LCM

• 약수: 어떤 수를 나누어떨어지게 하는 수
• 배수: 어떤 수의 1, 2, 3, ...n 배하여 얻는 수
• 공약수: 둘 이상의 수의 공통인 약수
• 공배수: 둘 이상의 수의 공통인 배수
• 최대 공약수(GCD. Greatest Common Divisor): 둘 이상의 공약수 중에서 최대인 수
• 최소 공배수(LCM. Least Common Multiple): 둘 이상의 공배수 중에서 최소인 수

LCM

GCD

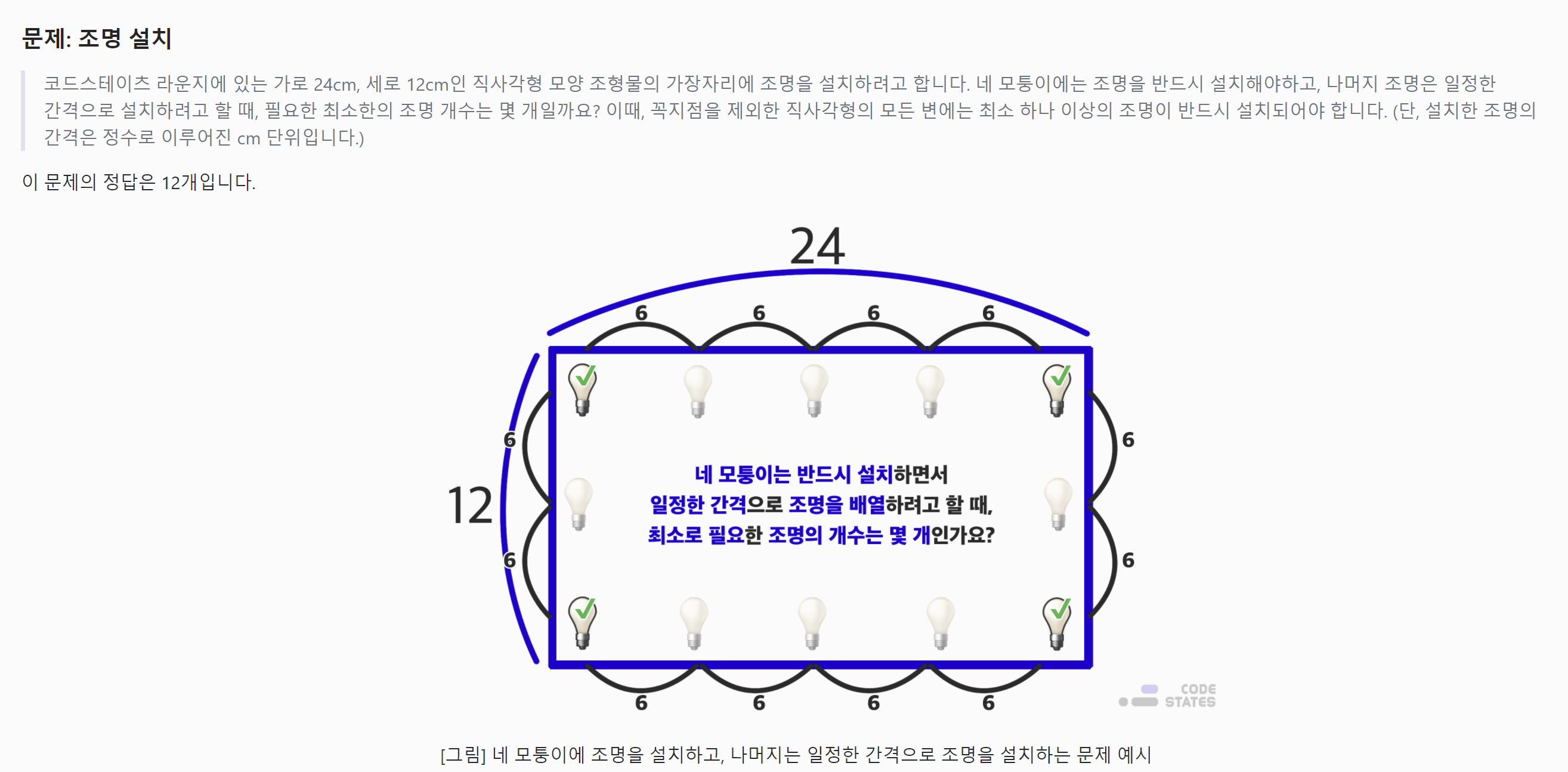
• GCD 코플릿 문제
  
  입출력예시

let M = 4;
let N = 8;
let output = divideChocolateStick(M, N);
console.log(output);
// [[1, 4, 8], [2, 2, 4], [4, 1, 2]]

Code

// 최대 공약수(유클리드 호제법: Euclidean algorithm)
function gcd(m, n) {
  if (m % n === 0) return n;
  return gcd(n, m % n);
}

function divideChocolateStick(M, N) {
  const result = [];
  // 최대공약수를 구한다.
  // M, N의 순서는 상관없다.
  const GCD = gcd(M, N);
  let temp = 0; //

  // 약수는 대칭적이므로 제곱근까지만 반복해도 된다.
  // 예) 36의 약수는 1, 2, 3, 4, 6, 9, 12, 18, 36이다.
  // 제곱근을 기준으로 양쪽의 값 하나씩 곱했을 때 36이 되기 때문에
  // 제곱근 보다 큰 약수는 제곱근보다 작은 약수에서 구할 수 있다.
  const sqrt = Math.floor(Math.sqrt(GCD));
  for (let left = 1; left <= sqrt; left++) {
    if (GCD % left === 0) {
      // 최대공약수의 약수인 경우 중 제곱근 보다 작은 약수의 경우
      result.push([left, M / left, N / left]);
      if (left * left < GCD) {
        // 제곱근이 아닌 경우(제곱근 보다 작은)
        right = GCD / left; // 최대 공약수를 제곱근이 아닌 수로 나누면 제곱근 보다 큰 약수를 구할 수 있다.
        result.push([right, M / right, N / right]);
      }
    }
  }

  // '빼빼로를 받게 되는 직원의 수'를 기준으로 오름차순으로 정렬
  result.sort((op1, op2) => op1[0] - op2[0]);

  return result;
}