Algorithm with Math - 순열 / 조합

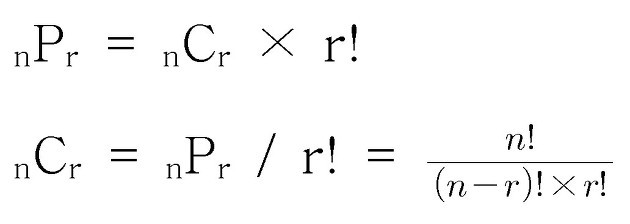
조합 - 순서에 상관없이 선택한다.

순열로 구할 수 있는 경우를 찾습니다.
순열로 구할 수 있는 경우에서 중복된 경우의 수를 나눕니다.
(5 X 4 X 3 X 2 X 1) / ((3 X 2 X 1) X (2 X 1)) = 10
5C3 = 5! / (3! * 2!) = 10

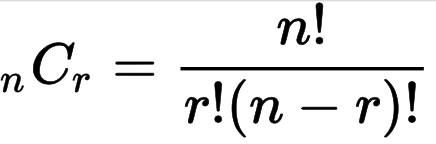
• 문제: 일곱 난쟁이
  왕비를 피해 일곱 난쟁이와 함께 평화롭게 생활하고 있던 백설 공주에게 위기가 찾아왔습니다. 하루일과를 마치고 돌아온 "일곱" 난쟁이가 "아홉" 명이었던 겁니다. 아홉 명의 난쟁이는 모두 자신이 "백설 공주와 일곱 난쟁이"의 주인공이라고 주장했습니다. (뛰어난 수학적 직관력을 가지고 있던) 백설 공주는 일곱 난쟁이의 키의 합이 100임을 기억해 냈습니다. 아홉 난쟁이 각각의 키가 주어질 때, 원래 백설 공주와 평화롭게 생활하던 일곱 난쟁이를 찾는 방법은 무엇인가요?

• 위 문제는 조합을 이용해서 일곱 난쟁이를 찾을 수 있습니다. 모든 일곱 난쟁이의 키를 합했을 때 100이 된다고 주어졌기 때문에, 9명의 난쟁이 중 7명의 난쟁이를 순서를 생각하지 않고, 난쟁이 7명의 키를 합했을 때 100이 되는 경우를 찾으면 됩니다.

순열 - 순서에 상관있이 선택한다.

• 5개중에 3개를 고르는 방법
  첫번째 선택하는 방법에는 다섯 가지가 있습니다.
  첫번째 선택을 하고 난 뒤에, 두번째 선택하는 방법에는 네 가지가 있습니다.
  두번째 선택을 하고 난 뒤에, 세번째 선택하는 방법에는 세 가지가 있습니다.
  5 X 4 X 3 = 60
5P3 = (5 X 4 X 3 X 2 X 1) / (2 X 1) = 60
  

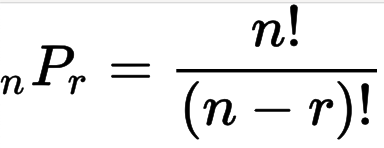
• 문제: 소수 찾기
  한 자리 숫자가 적힌 종잇조각이 흩어져 있습니다. 흩어진 종잇조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다. 종이에 기록된 모든 숫자가 배열로 주어진다면, 이 종잇조각으로 만들 수 있는 소수는 몇 개인가요?

• 숫자는 순서에 의해 전혀 다른 값이 될 수 있습니다. 예를 들어 123과 321은 전혀 다른 숫자입니다. 만약 이 문제를 조합으로 접근하게 된다면, 123과 321은 같은 경우로 취급합니다. 따라서, 순서를 고려하지 않고 k 개를 뽑아내는 조합으로는 이 문제를 해결할 수 없습니다.

• n 개의 숫자 중에 1~k 개를 뽑아서 순열을 생성합니다.

• 각 순열을 정수로 변환하고, 해당 정수가 중복되지 않으면서 동시에 소수인지 검사합니다.

• 소수이면 개수를 셉니다.

중복순열은 무엇인가 ?

• 요소를 반복해서 쓸수 있는것 !!

for 반복문

3개중에 3개를 뽑아서 중복순열을 만들어보자

function forloop(){
  let result = [] ;
  let lookip = [1,2,3];
  
  for(let i=0; i<3; i++){
    let pick1 = lookup[i]
      for(let j=0; j<3; j++){
        let pick2 = lookup[j]
          for(let k=0; k<3; k++){
            let pick3 = lookup[k]
               result .push([pick1, pick2, pick3])
             }
          }
      }
      return result;
  }
// 위와 같은 코드
function forloop(){
  let result = [] ;
  let lookip = [1,2,3];
  
  for(let i=0; i<3; i++){
      for(let j=0; j<3; j++){
         for(let k=0; k<3; k++){
             result .push([lookup[i], lookup[j], lookup[k]])
             }
          }
      }
      return result;
  }

3개중에 2개를 뽑아서 중복순열을 만들어보자

function forloop(){
  let result = [] ;
  let lookip = [1,2,3];
  
  for(let i=0; i<3; i++){
      for(let j=0; j<3; j++){
             result .push([lookup[i], lookup[j]])
          }
      }
      return result;
  }

재귀함수를 사용

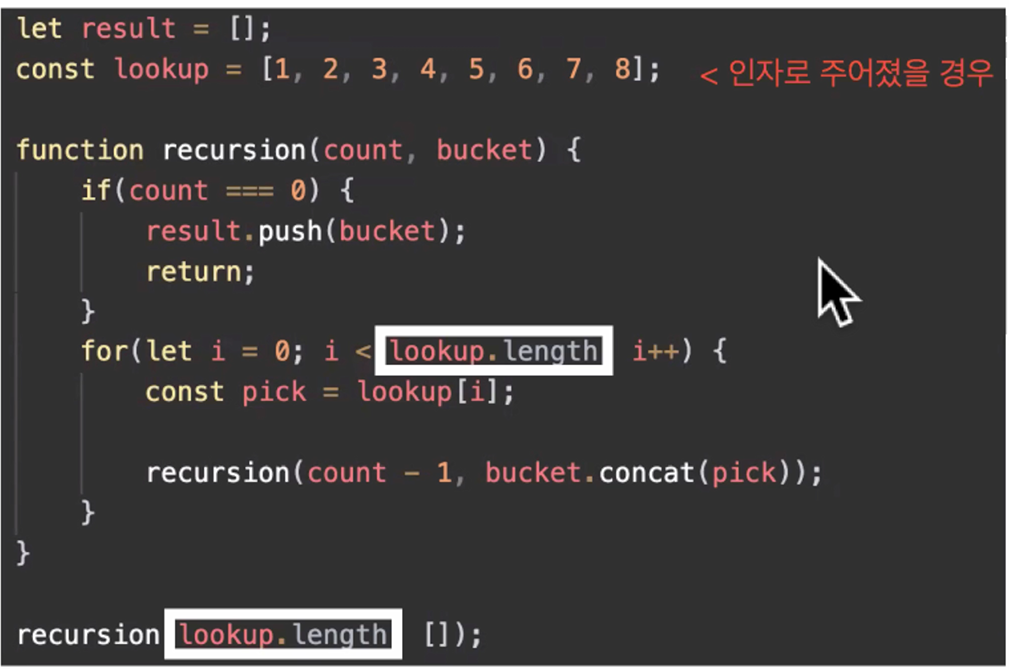
3개중에 3개를 뽑아서 중복순열을 만들어보자

let result = [];
let lookup = [1,2,3];

function recursion(count, bucket){
  if(count =0){
    result.push(bucket);
    return;
  }
  for(let i=0; i<3; i++){
    const pick =lookup[i];
    recursion(count-1, bucket.concat(pick)); // push 말고 concat을 사용하는 이유 push를 쓰면 길이의 값이 반환되기 때문에 매개변수로 적절한 값이 들어가지 않는다.
  }
}
recursion(3, []);

n개중에 n개를 뽑아서 중복순열을 만들어보자

관련 코플릿 : rockPaperScissors

문제
가위바위보 게임은 2인 이상의 사람이 동시에 '가위, 바위, 보'를 외치고 동시에 가위, 바위 또는 보 중에서 한 가지를 의미하는 손 모양을 내밀어 승부를 결정짓는 게임입니다. 세 판의 가위바위보 게임을 할 경우, 한 사람은 세 번의 선택(예. 가위, 가위, 보)을 할 수 있습니다. 세 번의 선택으로 가능한 모든 경우의 수를 구하는 함수를 작성합니다.

입출력 예시

let output = rockPaperScissors();

console.log(output);
/*
    [
      ["rock", "rock", "rock"],
      ["rock", "rock", "paper"],
      ["rock", "rock", "scissors"],
      ["rock", "paper", "rock"],
      // ...etc ...
    ]
  */
  
 let output = rockPaperScissors(5);

console.log(output);
/*
    [
      ["rock", "rock", "rock", "rock", "rock"],
      ["rock", "rock", , "rock", "rock", "paper"],
      ["rock", "rock", , "rock", "rock", "scissors"],
      ["rock", "rock", "rock", "paper", "rock"],
      ["rock", "rock", "rock", "paper", "paper"],
      ["rock", "rock", "rock", "paper", "scissors"],
      ["rock", "rock", "rock", "scissors", "rock"],
      // ...etc ...
    ]
  */

사고하는 방법
1. 한번씩은 요소가 들어가야 한다.
2. 그렇다면 순회해야 한다. -> 반복문!!! or 재귀 !!!

Code

const rockPaperScissors = function(n) {
  let result = [];
  let rps = [['rock'], ['paper'], ['scissors']];
  if (n === undefined) n = 3;
  // n이 없을 때 처리해줘야 됨
  if (n === 1) return [['rock'], ['paper'], ['scissors']];

  let prev = rockPaperScissors(n - 1);

  for (let i = 0; i < rps.length; i++) {
    for (let j = 0; j < prev.length; j++) {
      result.push([...rps[i], ...prev[j]]);
    }
  }
  return result;
};

reference code

// Advanced가 포함된 레퍼런스 코드입니다.
const rockPaperScissors = function (rounds) {

  // rounds 매개변수를 임의로 넣습니다.
  // rounds 변수가 있을 경우 그대로 사용하고, 없다면 3(기본)을 사용합니다.
  rounds = rounds || 3;
  const rps = ['rock', 'paper', 'scissors'];

  // 결과를 담을 배열 선언
  const outcomes = [];

  // 재귀를 사용할 함수 선언
  // rounds를 넣을 변수 roundsToGo, 일회용 배열인 playedSoFar 변수를 선언합니다.

  // 재귀를 사용하는 이유는, 배열의 모든 요소의 경우의 수를 훑기 위한 적절한 방법이기 때문입니다.
  // 간단히 말하자면, 이 함수는 rounds 숫자를 기준으로, 일회용 배열에 rps 요소를 rounds 숫자만큼 넣게 됩니다.
  // 이 로직을 잘 이해할 수 있을 때까지 하단의 함수 로직을 연구해야 합니다.
  let permutate = function (roundsToGo, playedSoFar) {

    // rounds가 0일 경우 outcones 배열에 삽입하고, 재귀에서 빠져나옵니다.
    if (roundsToGo === 0) {
      outcomes.push(playedSoFar);
      return;
    }

    // rps 배열을 한 번씩 순회합니다.
    for (let i = 0; i < rps.length; i++) {
      // rps의 i번째 요소를 변수에 담아서
      let currentPlay = rps[i];
      // permutate(본인)에 기존 rounds에서 하나 뺀 숫자와, 일회용 배열 playedSoFar에 currentPlay를 삽입하여 재귀를 실행합니다.
      // rounds에서 하나를 빼는 이유는, 일회용 배열의 크기를 rounds만큼 맞춰주기 위함입니다. [rock, rock, rock]

      // Q. playedSoFar.push(currentPlay)로 할 수 있을 텐데, 왜 concat을 사용할까요?
      permutate(roundsToGo - 1, playedSoFar.concat(currentPlay));
      /**
       * 이 재귀의 로직은 이렇습니다. 처음 실행된 반복문은 rps를 전부 순회해야 끝이 납니다.
       * 그러나 한 번 반복할 때마다 permutate 함수가 실행되고, rounds의 숫자는 짧아지며, playedSoFar에 요소가 계속 쌓일 것입니다.
       * 결국, roundsToGo가 0이 될 때까지 이 반복문은 rps[i]가 0일 것이며, playedSoFar에는 [rock, rock, rock]이 되어 outcones에 Push하고, 종료하게 됩니다.
       * return이 되었으니, 한 번의 재귀 호출이 끝났습니다. 마지막 호출 바로 전으로 돌아가,
       * for문은 i = 1을 가리키게 될 것이고, [rock, rock, paper]을 삽입한 뒤 호출을 하게 됩니다.
       * roundsToGo가 0이 되어, 해당 배열은 outcomes 배열에 삽입됩니다.
       * 이런 식으로 모든 호출의 반복문이 끝날 때까지 반복하며 outcomes에 경우의 수 요소들이 담기게 됩니다.
       */
    }
  };

  // 함수를 실행합니다.
  permutate(rounds, []);

  // outcomes를 반환합니다.
  return outcomes;
};

순열을 만드는 법

3개중에 3개를 뽑아서 중복순열을 만들어보자

function forloop(){
  let result = [] ;
  let lookip = [1,2,3];
  
  for(let i=0; i<3; i++){
      for(let j=0; j<3; j++){
         for(let k=0; k<3; k++){
           if(i === j || j ===k || k ===i) continue;
             result .push([lookup[i], lookup[j], lookup[k]])
             }
          }
      }
      return result;
  }
// 중복된 요소를 피하고 중복되지 않는 것만 넣음
// 중복이든 아니든 일단 실행을 시키고 , 중복된걸 마지막에 쳐낸다.

관련 코플릿 : 새로운 치킨 소스 레시피

문제
개업 이래로 항상 승승장구하는 '승승장구 치킨집'의 비결은 소스에 있다. 수많은 타사 브랜드 치킨집들이 승승장구 치킨집의 소스 비결을 알아내려고 했으나 빈번히 포기했다.
그 이유는 5대째 내려오는 '비밀의 승승장구 치킨 소스 비율 레시피'는 70억 인구 중 사장님만 알고 있기 때문이다. 최근, 누리꾼 사이에서 이 레시피의 일부분을 발췌했다는 소문을 듣게 되었다.
그 소문은 다음과 같다.

• N 가지의 재료 중에 단 M 가지만을 사용하여 조합한 모든 경우의 수 중 하나이다.
• 재료는 0과 1로만 이루어진 숫자로 암호화가 되어 있고, 항상 1로 시작하며 복호화를 할 수 없다.
  단, 0이 3개 이상인 재료는 상한 재료이기 때문에 제외한다.
• 재료의 순서에 따라 맛이 달라지기 때문에, 재료를 넣는 순서가 다르다면 다른 레시피이다.

이 소문을 참고하여 '비밀의 승승장구 치킨 소스'가 될 수 있는 경우의 수를 모두 반환하는 함수를 작성하세요.

입출력예시

const output1 = newChickenRecipe([1, 10, 1100, 1111], 2);
console.log(output1);
/*
  [
    [1, 10], [1, 1100], [1, 1111],
    [10, 1], [10, 1100], [10, 1111],
    [1100, 1], [1100, 10], [1100, 1111],
    [1111, 1], [1111, 10], [1111, 1100]
  ];
*/

const output2 = newChickenRecipe([10000, 10, 1], 3);
console.log(output2); // []

const output3 = newChickenRecipe([11, 1, 10, 1111111111, 10000], 4);
console.log(output3);
/* 
  [
    [1, 10, 11, 1111111111],
    [1, 10, 1111111111, 11],
    [1, 11, 10, 1111111111],
    [1, 11, 1111111111, 10],
    [1, 1111111111, 10, 11],
    [1, 1111111111, 11, 10],
    [10, 1, 11, 1111111111],
    [10, 1, 1111111111, 11],
    [10, 11, 1, 1111111111],
    [10, 11, 1111111111, 1],
    [10, 1111111111, 1, 11],
    [10, 1111111111, 11, 1],
    [11, 1, 10, 1111111111],
    [11, 1, 1111111111, 10],
    [11, 10, 1, 1111111111],
    [11, 10, 1111111111, 1],
    [11, 1111111111, 1, 10],
    [11, 1111111111, 10, 1],
    [1111111111, 1, 10, 11],
    [1111111111, 1, 11, 10],
    [1111111111, 10, 1, 11],
    [1111111111, 10, 11, 1],
    [1111111111, 11, 1, 10],
    [1111111111, 11, 10, 1],
  ]
*/

Code

function newChickenRecipe(stuffArr, choiceNum) {
  const freshArr = [];

  for(let i=0; i<stuffArr.length; i++){
    const findDecay = String(stuffArr[i]).split('').filter((el)=>el=== '0');
    if(findDecay.length <=2){
      freshArr.push(stuffArr[i])
    }
  }

  if (freshArr.length === 0 || freshArr.length < choiceNum){
    return [];
  } 

  function permutation(arr, num) {
    if (num === 1) return arr.map(i => [i]);
    return arr.reduce((acc, target, idx, origin) => {
      const rest = origin.slice();
      rest.splice(idx, 1);
      const pArr = permutation(rest, num - 1);
      const addArr = pArr.map(el => [target, ...el])
      acc.push(...addArr);
      return acc;
    }, [])
  }

Reference Code

function newChickenRecipe(stuffArr, choiceNum) {
  // stuffArr에서 0이 3개 이상이라면 전부 필터로 거르기.
  let freshArr = [];

  for (let i = 0; i < stuffArr.length; i++) {
    const element = String(stuffArr[i])
      .split('')
      .filter((e) => e === '0');
    if (element.length <= 2) {
      freshArr.push(stuffArr[i]);
    }
  }

  // 정렬
  freshArr.sort((a, b) => a - b);

  // 엣지 케이스 처리
  if (freshArr.length === 0 || freshArr.length < choiceNum) return [];

  // 레시피 초기화
  let result = [];

  // freshArr를 상대로 순열 구하기
  const permutation = (arr, bucket, n) => {
    if (n === 0) {
      result.push(bucket);
      return;
    }

    for (let i = 0; i < arr.length; i++) {
      // 하나를 초이스함
      const choice = arr[i];
      // 배열을 슬라이스함
      const sliceArr = arr.slice();
      // 초이스만 뺀다
      sliceArr.splice(i, 1);
      // 재귀
      permutation(sliceArr, bucket.concat(choice), n - 1);
    }
  };

  // 실행
  permutation(freshArr, [], choiceNum);
  
  // 순열의 길이 반환
  return result;
}

조합을 만드는 법

function forloop(){
  let result = [] ;
  let lookip = [1,2,3];
  
  for(let i=0; i<3; i++){
      for(let j=i+1; j<3; j++){
             result .push([lookup[i], lookup[j]])
          }
      }
      return result;
  }
  // [1,2,3] - > 
  [1,2] ,[1,3 ] 이후에는 1로 만들수 있는것을 고려할 필요가 없다.

관련 코플릿 : 블랙잭은 지겨워

문제
평범한 블랙잭 게임에서 수시로 패배하자 흥미가 떨어진 김코딩은 박타짜에게 게임룰을 변형하여 새로운 카드 놀이를 해 볼 것을 제안합니다.
새로운 룰은 다음과 같습니다.

예로, [1, 2, 3, 4]라는 카드를 받았을 때 만들 수 있는 숫자는 6, 7, 8, 9이고, 소수는 7 하나이기 때문에 가지고 있는 소수의 개수는 1개입니다.
[2, 3, 4, 8, 13]라는 카드를 받았을 때 만들 수 있는 숫자는 9, 13, 18, 14, 19, 23, 15, 20, 24, 25이고, 소수는 13, 19, 23 총 3개이기 때문에 가지고 있는 소수의 개수는 3개입니다.

게임을 진행하기 전에 소수에 대해 아무런 지식이 없는 박타짜는 게임을 며칠 미룬 뒤, 게임의 룰을 따르는 함수를 만들기로 했습니다.
소수에 약한 박타짜를 도와 여러 장의 카드 중 세 장씩 조합해 소수가 되는 경우의 수를 리턴하는 함수를 완성해 주세요.

입출력예시

let output = boringBlackjack([1, 2, 3, 4]);
console.log(output); // 1

let output = boringBlackjack([2, 3, 4, 8, 13]);
console.log(output); // 3

Code

function boringBlackjack(cards) {
    const isPrime = (num) => {
    for(let i = 2; i<num/2; i++){
      if(num % i === 0) return false;
    }
    return true;
  }
  let arr = []
  for(let i = 0; i<cards.length; i++){
    for(let j = i+1; j<cards.length; j++){
      for(let k = j+1; k<cards.length;k++){
        let add = cards[i] + cards[j] + cards[k];
        arr.push(add); 
        arr = arr.filter((el)=>{
          if(isPrime(el)) return el;
        })
      }
    }
  }
  return arr.length;
  // TODO: 여기에 코드를 작성합니다.
}

Reference Code

function boringBlackjack(cards) {
  let count = 0;

    // 1. cards 에서 카드 3장 뽑기
    let length = cards.length;
    // 카드 뽑는 방식은 첫 카드를 cards 의 0번 index 부터 고정해 놓고 1씩 뒤로 옮겨간다
    for (let i = 0; i < length; i++) {
    // 두 번째 카드의 인덱스는 첫 카드 + 1에서 시작해야 하고
      for (let j = i + 1; j < length; j++) {
    // 세 번째 카드의 인덱스는 두 번째 카드 + 1에서 시작해야 한다 
        for (let k = j + 1; k < length; k++) {
          const number = cards[i] + cards[j] + cards[k];
          // 세 카드의 합이 소수이면 경우의 수 + 1
          if (isPrime(number)) count++;
        }
      }
    }
  
    //2. 소수 판별
    function isPrime(number) {
    // 2부터 비교하기 시작해서 나누어 떨어지는 수가 있으면 소수가 아니다
    // for 문 조건을 number/2 로 해도 되는 이유는 i > number/2 가 되면 몫이 절대 0이 될수 없기 때문에
    // number/2 까지만 비교해 보아도 소수 판별이 가능하다
      for (let i = 2; i < number/2; i++) {
        if (number % i === 0) return false;
      }
      return true;
    }
  
    return count;
}

Pick or not (응용)

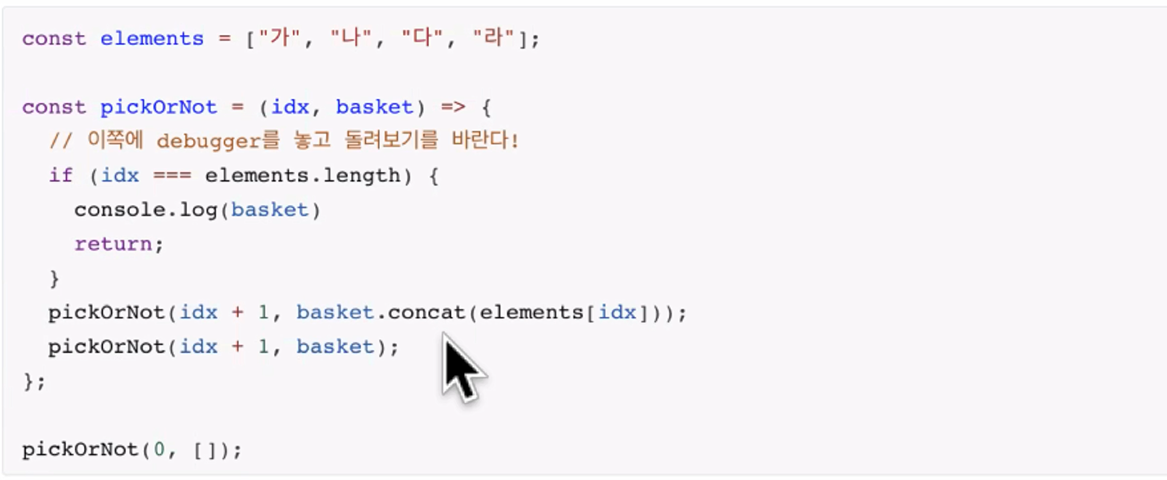
결론

(1)
중복순열: 모든 요소를 다넣음!
순열: 순열과 로직은 같지만 마지막이나 중간에서 중복된 요소가 있다.
조합: 순서를 지켜서 뽑음

(2)
7p5일 경우 5중포문을 만들어야 한다 !!
하지만 너무길다...
혹은 npr 인 경우에 ??
재귀가 필요하다!!!