1.학습한 내용

1) SVM

support vector machines

무한 차원 공간에서 초평면 또는 초평면 세트를 구성한다.

margin 이 클수록 좋은 분리가 가능하다.
이때의 공간을 support 공간이 된다.

선으로 나눌때, 2차원으로는 나눌수 없을때
3차원으로 생각하여 나눌수있게된다.

2차원일때는 1차원(선)으로 나누지만
3차원으로 가면 2차원(면)으로 나누게된다

이런식으로 저차원에서 분류를 할수없던것을 고차원으로 옮겨서 분류를 할수있도록 도와주는 도구이다.

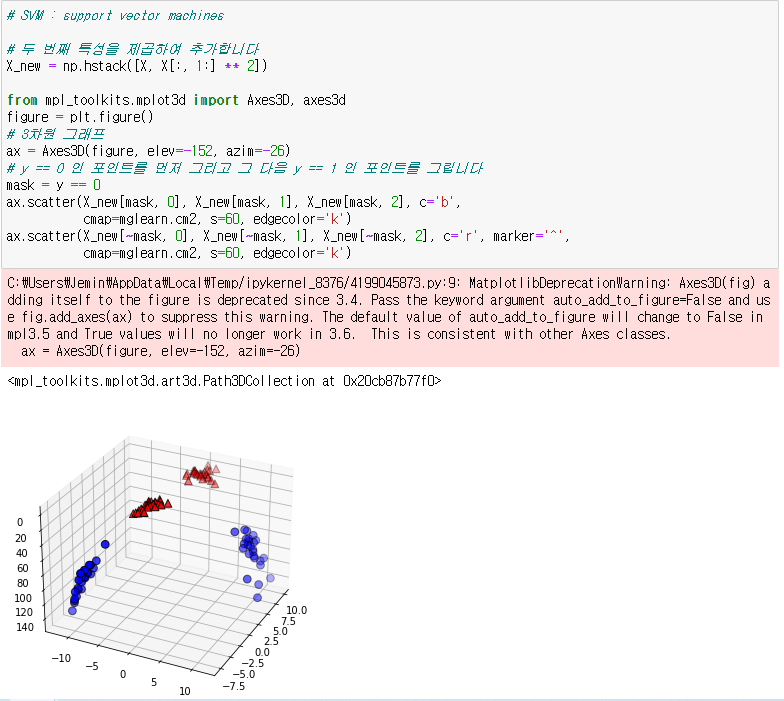
# 두 번째 특성을 제곱하여 추가합니다
X_new = np.hstack([X, X[:, 1:] ** 2])

from mpl_toolkits.mplot3d import Axes3D, axes3d
figure = plt.figure()
# 3차원 그래프
ax = Axes3D(figure, elev=-152, azim=-26)
# y == 0 인 포인트를 먼저 그리고 그 다음 y == 1 인 포인트를 그립니다
mask = y == 0
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
           cmap=mglearn.cm2, s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^',
           cmap=mglearn.cm2, s=60, edgecolor='k')

이전날 2차원에서 2그룹으로 나뉘었던 군집들이
3차원으로 바뀌면서 더 분류하기 쉽도록 보이게 된것을 볼수있다.

2) Deep Learning

한개의 node 로 계산하기 힘든것들을
여러개의 node를 연결한 인공신경망을 통해서 계산할수 있게 되었다.

이때 오늘날 사용하는 Deep Learning Framework 로는

TensorFlow

google, 핵심코드가 C++로 작성
뛰어난 이식성 및 확장성
진입장벽 다소 높음.

Keras

직관적이고 쉬운 API
TensorFlow 를 Backend로 활용
동일한 코드로 CPU,GPU에서 실행 가능

Pytorch

Facebook,
C/CUDA backend 로 사용
진입장벽이 낮음 파이썬 문법과 유사
GPU 가속 연산

완전 연결계층(Fully-connected Layer)

모든 노드 들이 서로 연결된 신경망
Dense Layer 라고도 불림.

Input layer -> (hidden layer) -> output layer

이때 인풋과 아웃풋은 볼수있지만, hidden layer 부분은 볼수가없다.
(중간과정)

hidden layer 가 많을수록 복잡하다.

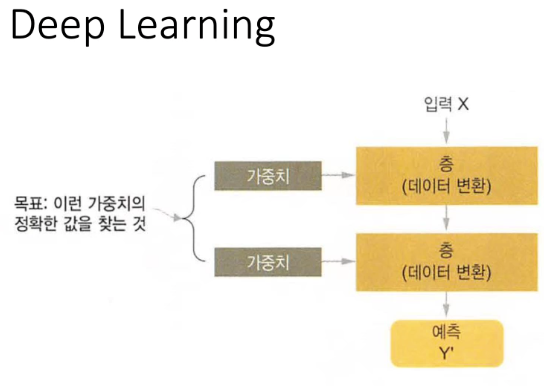
딥러닝의 목표:

가중치를 찾아내는것이 목표.

입력 x1 -> 가중치입력-> 데이터변환층
-> 가중치입력 ->데이터 변환층 -> 예측값 y1

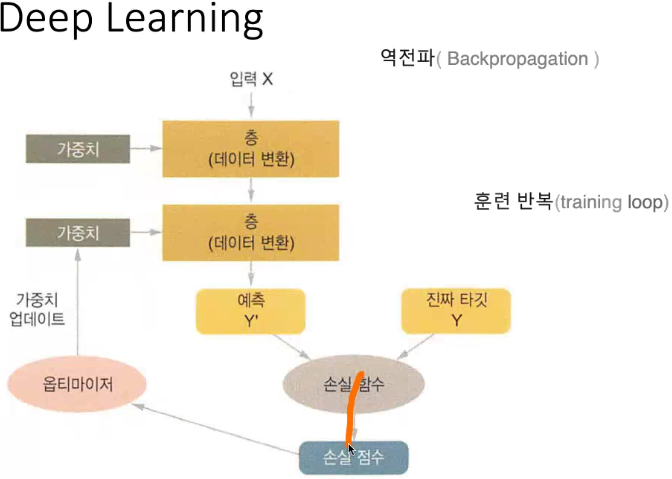
실제타깃 y2

y1과 y2 의 차이를 비교 -> 손실함수
손실함수(Loss Function)를 통해서 손실점수를 측정

그 측정된 손실점수를 바탕으로 가중치에 옵티마이저 값으로 업데이트를 하여 다시 반복한다.

이때 가중치의 정확한 값을 구하기 위해서

2-1) 수학적인 기법 math

1차함수, 2차함수 3차함수, 편미분등의 수학적인 기법이 사용될수있다.

이를 확인하기 위해서 기본적인 라이브러리를 불러온다.

import math

import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')

그리고 1차함수의 경우 간단하게 정의가 가능하다.

def linear_function(x):
    a=0.5
    b=2
    return a*x+b

이를 사용 하여 스칼라값을 입력하면

print(linear_function(5))

1차함수를 사용할수 있고, 이를 시각화 하고자하면

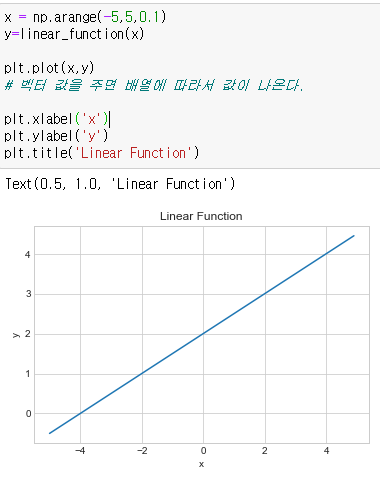
x = np.arange(-5,5,0.1)
y=linear_function(x)

plt.plot(x,y)

plt.xlabel('x')
plt.ylabel('y')
plt.title('Linear Function')

x의 범위를 지정하면 x의 배열만큼 값이 나오며, 이를 그래프로 그리게 되면

직선의 형태가 나오는 것을 알수있다.

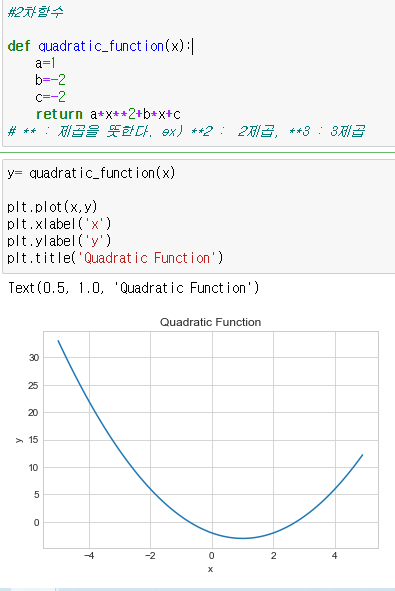
마찬가지로 2차,3차함수의 경우에도

def quadratic_function(x):
    a=1
    b=-2
    c=-2
    return a*x**2+b*x+c

정의를 하고

y= quadratic_function(x)

plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Quadratic Function')

입력을 하는것으로

나오는 것을 확인할수있다.

def cubic_function(x):
    a=4
    b=0
    c=-1
    d=-8
    return a*x**3+b*x**2+c*x+d

y= cubic_function(x)

plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Cubic_function')

2-1) 신경망 데이터 표현

Tensor (텐서)

정보의 단위이다.(tensor)

ex)
1d array : (4,) 1차원텐서
2d array : (2,3) 2차원텐서
3d array : (1,2,3) 3차원텐서

예를들어 스칼라값의 경우에는 0차원 텐서이다.

x = np.array(3)
print(x)

print(x.shape)

print(np.ndim(x))

그리고 리스트의 경우에는 1차원 텐서를 가진다.

a = np.array([1,2,3,4])
b = np.array([5,6,7,8])

c=a+b
print(c)
print(c.shape)
print(np.ndim(c))

이때 스칼라와 벡터값을 곱하는 경우, 벡터값과 다르게 부족한 부분이 있는 스칼라의 경우 나머지 부분을 벡터에 맞게 복사가 되어 입력되는데, 이것을 brodcasting 이라고 한다.

m= np.array(10)
d= a*m
print(d)
print(d.shape)
print(np.ndim(d))

행렬의 경우에는 행과 열로 이루어진 2차원 텐서이다.

a = np.array([[1,2],[3,4]])
b = np.array([[10,10],[10,10]])

print(a)
print(a.shape)
print(np.ndim(a))

print(a*b)

필요에 따라서 행과 열을 바꿔어야 하는 일이 생기는데 이러한 작동을 전치행렬이라고 하며 T로 작동한다.

a=np.array([[1,2,3],[4,5,6]])

a_ = a.T

print(a_)

3차원의 데이터 또한 만들어낼수있다.

X = np.array([[[5,3,2,1],
               [5,5,3,1],
               [6,1,2,3]],
              [[1,1,1,1],
               [3,4,7,5],
               [1,8,3,4]],
              [[10,9,3,9],
               [5,4,3,2],
               [7,6,3,4]]])


print('X\n', X, end='\n\n')
print('X.shape:', X.shape)
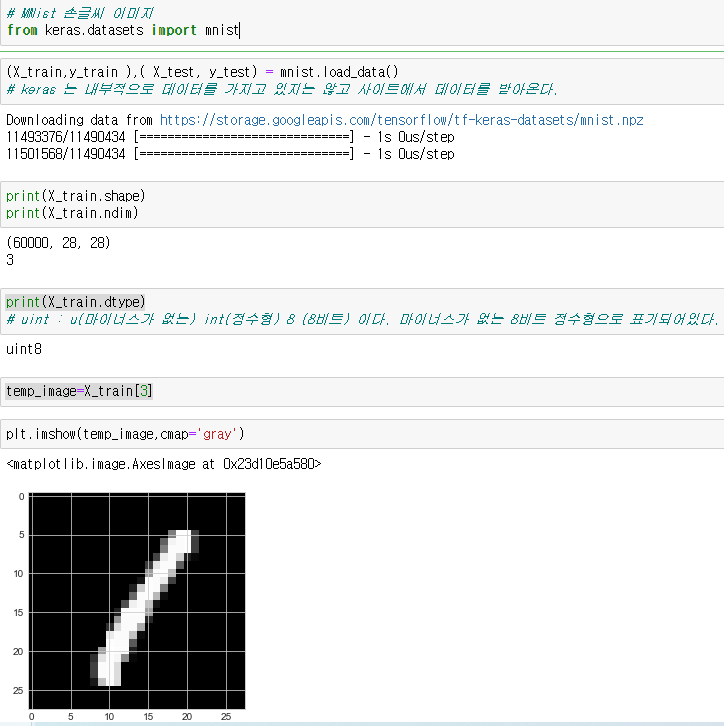
print('X.ndim:', X.ndim)

이후 이미지또한 X축, Y축, 그리고 RGB값을 통해서 3차원 데이터 이므로, 이를 불러낸다.

from keras.datasets import mnist
(X_train,y_train ),( X_test, y_test) = mnist.load_data()
print(X_train.shape)
print(X_train.ndim)
print(X_train.dtype)
temp_image=X_train[3]
plt.imshow(temp_image,cmap='gray')

2-2) 신경망 구조

퍼셉트론

인공신경망의 한 종류

다수의 입력과 가중치를 곱하여 그 값에 편항을 더한 값이 어느 임계치 값을 초과하면 활성화 함수를 통과한 출력값을 내보낸다.

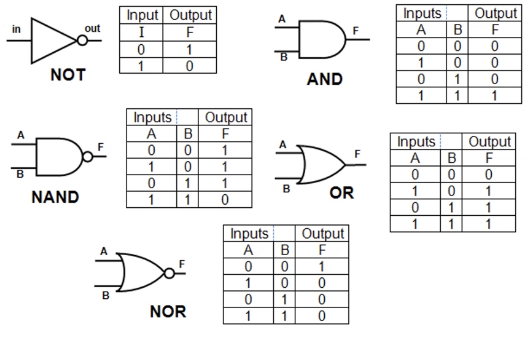
논리게이트(Logic Gates)

AND : 양쪽이 참일때 참, 그 외에는 거짓

OR:둘중에 하나라도 참이면 참

NOT : 무조건 반대로 출력

NAND: AND 의 반대, 양쪽이 참일때 거짓, 그외는 참

NOR:OR 의 반대, 둘중에 하나라도 거짓이면 거짓

이때의 논리게이트 또한 코드로 만드는것이 가능하다. 우선 필요한 라이브러리를 불러온다.

import numpy as np
import matplotlib.pyplot as plt
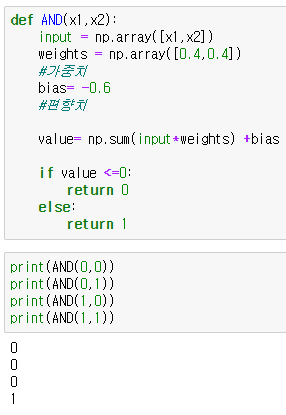
plt.style.use('seaborn-whitegrid')

AND 논리게이트

def AND(x1,x2):
    input = np.array([x1,x2])
    weights = np.array([0.4,0.4]) 
    #가중치
    bias= -0.6
    #편향치
    
    value= np.sum(input*weights) +bias
    
    if value <=0:
        return 0
    else:
        return 1
        
        print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))

이를 그래프를 통하여 확인할수 있다.

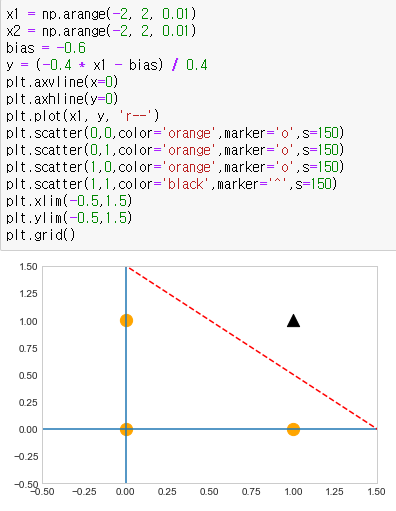
x1 = np.arange(-2, 2, 0.01)
x2 = np.arange(-2, 2, 0.01)
bias = -0.6
y = (-0.4 * x1 - bias) / 0.4
plt.axvline(x=0)
plt.axhline(y=0)
plt.plot(x1, y, 'r--')
plt.scatter(0,0,color='orange',marker='o',s=150)
plt.scatter(0,1,color='orange',marker='o',s=150)
plt.scatter(1,0,color='orange',marker='o',s=150)
plt.scatter(1,1,color='black',marker='^',s=150)
plt.xlim(-0.5,1.5)
plt.ylim(-0.5,1.5)
plt.grid()

이때 기준선의 위에있을때 1이 표시가 되는데,
둘다 1이 이상인 검은색 세모만이 1, 나머지는 0으로 출력된다.

OR 논리게이트

def OR(x1,x2):
    input = np.array([x1,x2])
    weights = np.array([0.4,0.4]) 
    
    bias= -0.3
        
    value= np.sum(input*weights) +bias
    
    if value <=0:
        return 0
    else:
        return 1
print(OR(0,0))
print(OR(0,1))
print(OR(1,0))
print(OR(1,1))

이때 AND 의 코드에서 bias , 편향치만을 조절을 하였는데 OR 논리게이트가 완성이 되었다.
이는 시각적으로 더 확실하게 확인할수 있게되는데.

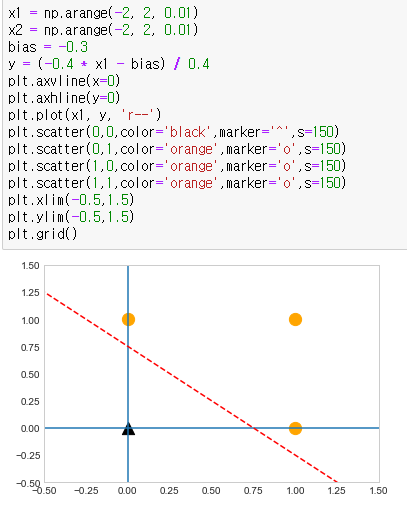
x1 = np.arange(-2, 2, 0.01)
x2 = np.arange(-2, 2, 0.01)
bias = -0.3
y = (-0.4 * x1 - bias) / 0.4
plt.axvline(x=0)
plt.axhline(y=0)
plt.plot(x1, y, 'r--')
plt.scatter(0,0,color='black',marker='^',s=150)
plt.scatter(0,1,color='orange',marker='o',s=150)
plt.scatter(1,0,color='orange',marker='o',s=150)
plt.scatter(1,1,color='orange',marker='o',s=150)
plt.xlim(-0.5,1.5)
plt.ylim(-0.5,1.5)
plt.grid()

y절편이라고 할수있는 bias,편향치를 낮춤으로써 기준선의 위치가 내려갔고, 그로인해서 기준선위의 점이 3개, 아래의 점이 1개로 차이가 나는것을 볼수있다.

NAND 논리게이트

def NAND(x1,x2):
    input = np.array([x1,x2])
    weights = np.array([-0.6,-0.6]) 
    
    bias= 0.7
        
    value= np.sum(input*weights) +bias
    
    if value <=0:
        return 0
    else:
        return 1
print(NAND(0,0))
print(NAND(0,1))
print(NAND(1,0))
print(NAND(1,1))

이번에는 bias 뿐만이 아니라 가중치 또한 바뀌게 되었다.

x1 = np.arange(-2, 2, 0.01)
x2 = np.arange(-2, 2, 0.01)
bias = 0.7
y = (0.6 * x1 - bias) / -(0.6)
plt.axvline(x=0)
plt.axhline(y=0)
plt.plot(x1, y, 'r--')
plt.scatter(0,0,color='orange',marker='o',s=150)
plt.scatter(0,1,color='orange',marker='o',s=150)
plt.scatter(1,0,color='orange',marker='o',s=150)
plt.scatter(1,1,color='black',marker='^',s=150)
plt.xlim(-0.5,1.5)
plt.ylim(-0.5,1.5)
plt.grid()

이를 통해서 AND 의 그래프와 비슷해 보이지만, (0,0) 과 (1,1) 의 값이 다르다는 것을 확인할수있었다.

지난 수업에서 2차원은 자료의 분류가 힘들어 진다는것을 알게되고, 이로 인해서 3차원으로 차원을 늘려서 2차원 면으로 분류를 하는 방식을 사용하였다.
이 또한 논리게이트에서 사용이 되었다.
기존에는 0 1 1 0 의 결과값을 확인하는것이 불가능 했으며, 이 문제를 XOR 이라고 불렀다.
그런데 이 문제또한 3차원으로 차원을 늘려서 2차원 면으로 분류를 하듯이
하나의 퍼셉트론이 아닌 여러개의 퍼셉트론,다층 퍼셉트론 (Multi Layer Perceptron , MLP) 을 사용하는것으로 해결을 하는것이 가능해졌다.

다층 퍼셉트론 (Multi Layer Perceptron , MLP)

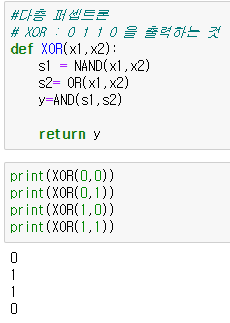
def XOR(x1,x2):
    s1 = NAND(x1,x2)
    s2= OR(x1,x2)
    y=AND(s1,s2)
    
    return y
    
print(XOR(0,0))
print(XOR(0,1))
print(XOR(1,0))
print(XOR(1,1))

NAND 논리게이트와 OR논리게이트 두가지를 사용하는것으로 기존에 표현할수 없었던 0 1 1 0 을 표현할수 있게 되었다.

3)Keras 케라스

많이 사용되는 deep learning framework 중 하나인 케라스를 사용한다.
이를 라이브러리에서 불러온다.

import keras
keras.__version__

이때 keras.version 으로 케라스의 버전을 알수있다.

from keras.datasets import mnist
(train_images,train_labels),(test_images,test_labels)= mnist.load_data()

mnist 데이터를 불러오고, 이를 분류한다.
그리고 그중에 4번째 데이터를 정의한뒤 그것을 이미지로 시각화 한다. 그리고 그때의 데이터의 라벨을 확인한다.

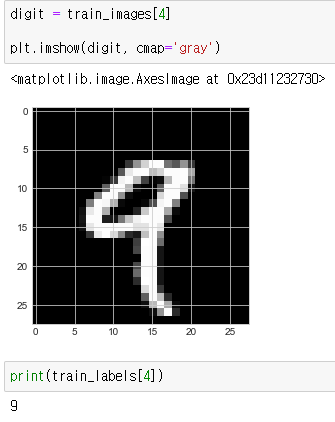
digit = train_images[4]

plt.imshow(digit, cmap='gray')

print(train_labels[4])

이를 통해서 4번째 데이터는 9의 형태를 가진 데이터이며, 라벨은 9인것을 알수있다.

2.학습내용 중 어려웠던 점

딥러닝을 시작하게 되면서, 논리게이트 등의 처음듣는 용어를 듣게 되고, 그를 코드로 구현한다고 했을때, 그에 대해서 지금까지 배운것을 바탕으로 생각을 해보았는데 어려웠다.

3.해결방법

이는 수업을 통해서 생각보다 간단한 코드로 만들수 있다는 점을 알게 되었다.

4.학습소감

이번수업을 통해서 이제 배운것을 활용하여서 함수를 짜고 사용하는것이 아니라, 특정한 목적을 위해서 함수와 코드를 짜는 작업이 제대로 시작하게 된것이라고 생각한다.

이를 제대로 이해하기 위해서는 그저 알려주는것을 듣고 사용하는것 뿐만이 아니라 활용을 하는것을 위해서 코드에 대한 분석을 하는것을 소홀히 하지않고 더 자세히 보는 것을 습관화 해야할것같다.