Machine Learning - Network Training

진수·2023년 9월 3일

Loss Function과 Accuracy

들어가기에 앞서 Optimizer을 설명하기 위해서는 Loss Function과 신경망 학습 과정을 알아야 한다.

Loss Function은 전체 네트워크의 weight가 얼마나 잘 설정되어 있는가를 보여준다.
즉, train 중 또는 train 후에 해당 네트워크가 예측하는 값과 실제 정답과 얼마나 차이가 나는지를 보여준다.

네트워크가 얼마나 잘 학습되었는지를 판단하는 지표는 그 네트워크가 수행하는 문제에 따라 달라지기도 한다. 예를 들어 회귀문제(Regression problem)의 경우 보통 연속적인 수를 결과로 나타내기 때문에 네트워크의 평가지표가 Loss Function그 자체인 MSE(평균 제곱 오차)를 사용한다.(다른걸 이용하기도 함) 하지만 분류문제는 정답이 1(맞음) 0(틀림)의 이진분류가 가능하다. 그래서 Accuracy라는 개념을 이용한다.

Loss function와 Accuracy는 실제 값과 예측값의 차이를 수치화 하는 함수이다. Loss를 구하는 방법은 여러가지가 있을 수 있다. 네트워크의 학습(Weight와 Bias의 업데이트)은 Loss(= cost) 값을 줄이는 방향으로 진행된다.
~~Loss와 cost는 완전히 같은 단어는 아니지만 대부분 비슷한 용어로 사용함~~

그렇다면 분류문제(Accuracy를 평가지표로 이용하는 네트워크)를 학습시킬 때 왜 Accuracy를 토대로 학습을 진행하지 않고 Loss Function을 이용하는지 다음을 통해 알아보자.

예를들어 train이 완료된 네트워크에 10개의 test data가 있다고 해보자, 그러면 Accuracy는 network에 따라 결과값이 다음과 같을것이다.

0(0/10), 0.1, 0.2, ... , 1(10/10)

분류 모델의 전체 네트워크 평가는 accuracy가 지표가 된다. 하지만 accuracy는 위에서 보듯이 불연속적인 값만을 가지게 되므로, 머리로는 1을 향해 가야한다는 것을 알지만 이를 컴퓨터에게 수식으로 1을 향해 가라 라고 말하려면 쉽지 않다. (쉽게 말하면 미분값이 거의 모든 부분에서 0이된다.) 그래서 Loss function을 설정하고 Loss function을 수치미분을 통해 Loss가 줄어드는 방향으로 학습을 진행할 수 있고, 어떤 알고리즘으로 Loss를 줄이는지는 Optimizer이 결정하는 것이다.

신경망 학습(Neural Network Training)

신경망 학습에 들어가기 전 데이터는 크게 세가지로 나눌 수 있다

Train data(훈련 데이터)
Valid data(유효 데이터)
Test data(테스트 데이터)

신경망의 학습이란 훈련 데이터로부터 신경망의 각 가중치와 편향을 조절하는 것을 의미한다. 학습은 데이터로부터 시작되고 데이터로부터 끝나게 되는 것이다.
이것은 큰 의미가 있는데 사람들이 물체를 인식하는 명확한 알고리즘을 제시할 수 없거나, 사람들이 인지하지 못하는 규칙이 있는 경우 인간의 분류보다 더 좋은 결과를 낼 수 있다.

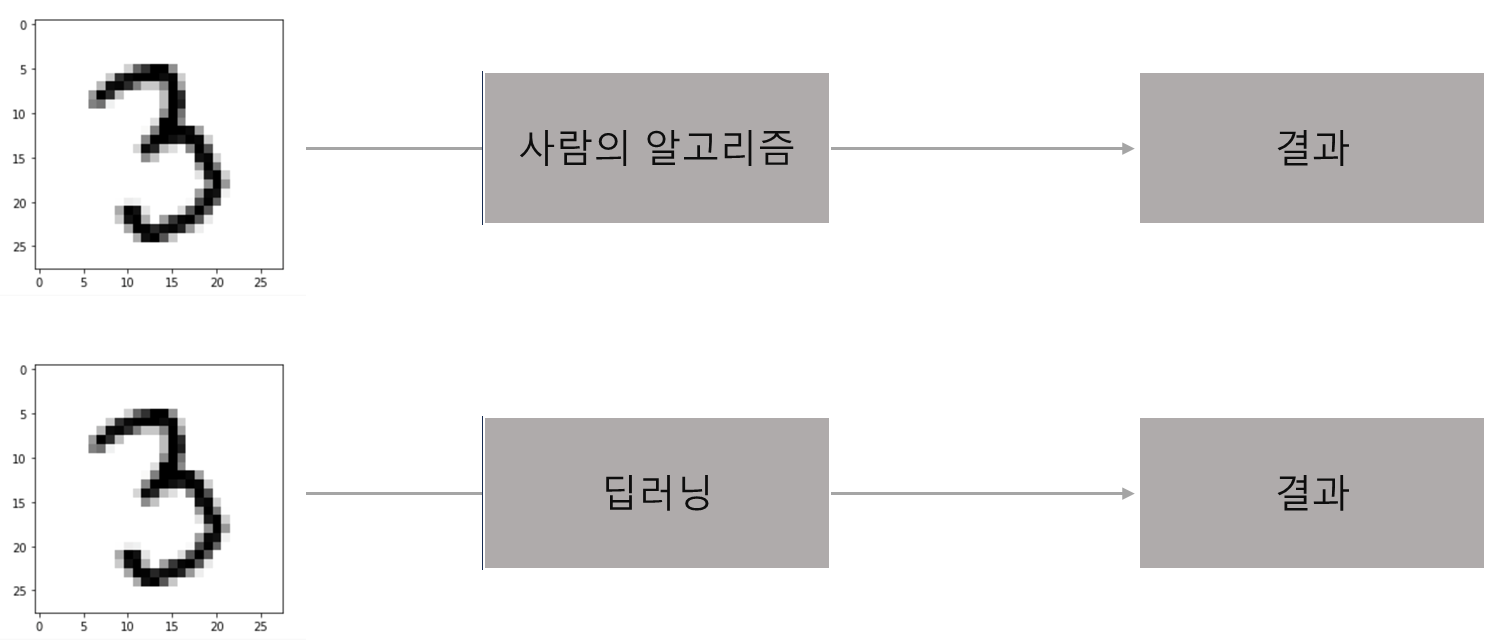
신경망의 학습 정도를 나타내기 위해서 손실함수(Loss Function)을 이용한다.
손실함수의 종류에는 MSE(평균 제곱 오차), CEE(교차 엔트로피 오차)등 여러가지가 있을 수 있다.

배치(Batch)

신경망을 학습할 때 하나의 데이터를 가지고 가중치를 조절할 수 있다. 그러나 만약 데이터가 MNIST같이 60000개의 훈련데이터가 있다면 가중치를 60000번 갱신하게 되는 것이고, 이는 매우 비효율적일 수 있다. 따라서 배치라는 것을 이용해 학습 횟수를 줄일 수 있다. 예를 들어 60000개의 데이터를 600개씩 하나의 배치로 묶게 되면, 학습은 60000/600 = 100번만 진행하게 된다. 이는 데이터의 양이 기하급수적으로 많아졌을 때, 과부하를 막을 수 있다.

에포크(Epoch)

전체 학습 횟수를 의미한다. 예를들어 100개의 데이터를 10개의 배치로 만들면 10번의 입력과 출력이 생길 것이고, 여기서 에포크를 5로 조절하게 되면 100개의 데이터를 5번 입출력하게되는것이다. 즉 총 학습 횟수는 50회가 된다.

total \enspace learning \enspace count = eopchs \ast total \enspace data/batch \enspace size

미니배치

미니배치는 많은 Train data 중에서 랜덤하게 소수의 데이터를 가지고 학습을 진행하는 것을 의미한다.

역전파(Back propagation)

신경망의 학습은 역전파를 이용해서 이루어진다. 역전파란 쉽게 말하면 데이터가 네트워크를 쭉 타면서 결과를 도출해내고, 다시 반대방향으로 가면서 가중치와 편향을 갱신하는것이다. 어떤식으로 이루어지는지 예시를 들면서 보자.

순전파로 계산을 하는 그래프를 먼저 살펴보자

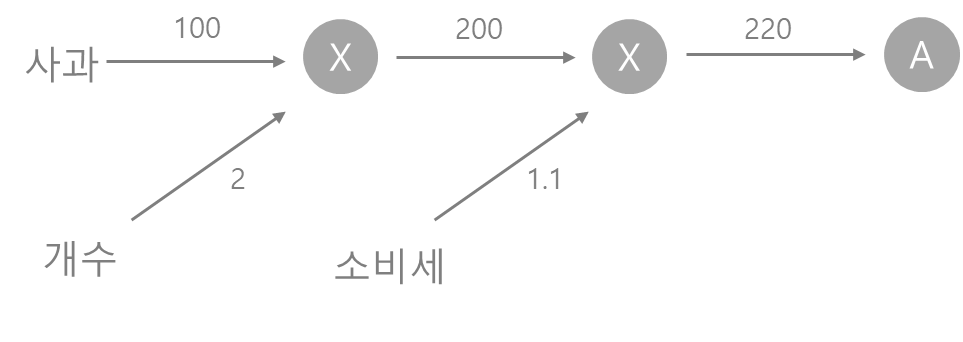
왼쪽에서 오른쪽으로 진행하면서 계산이 진행된다.

역전파는 이런식으로 거꾸로 곱셈이 진행되는 것을 볼 수 있다.
신경망의 학습은 이러한 역전파로 진행된다.

그렇다면 정확히 어떤 식으로 이루어지는지 수식을 통해서 알아보자.

x^2 + y^2 = z

이런 식이 존재한다. 이러면 그래프로 역전파를 나타내면 다음과 같다.

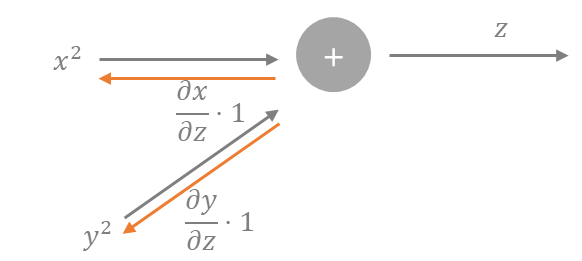
X와 Y로 전해지는 역전파는

\frac {\partial x}{\partial z},\frac {\partial y}{\partial z}

로 편미분의 꼴로 역전파가 전해진다.

이제 편미분으로 역전파가 전파된다는 것은 알았는데 도대체 어떤식으로 weight가 학습되는지를 알아보자.

학습률(learning rate)

학습률은 그 네트워크가 한 발짝식 걸어나갈 때 얼마나 큰 보폭으로 걸어나갈지를 결정하는 하이퍼 파라미터이다. 즉 사용자가 학습률을 적절한 수준으로 정해주어야 올바른 학습이 이루어진다.

Optimizer

Optimizer는 어떤 식으로 학습을 진행할 지를 결정하는 변수라고 볼 수 있다. 해결해야 하는 문제에 따라서 optimizer가 달라질 수 있지만 여기서 몇개만 소개하고 넘어가도록 하겠다.

SGD(확률적 경사 하강법)

W \gets W-\eta \frac{\partial L}{\partial W}

W는 가중치이고, 여기서 에타(n)은 학습률을 의미한다.
말 그대로 경사가 하강하는 방향으로 lr만큼 가중치를 갱신하는 방법이다.
그러나 이 방법에는 단점이 존재하는데, 안장점(saddle point)에 도달하게 되면, 기울기가 거의 0이 되기 때문에 학습이 더 이상 이루어지지 않는다는 점이 있다.
또한 lr을 적절하게 조절하지 않으면 너무 결과 값 까지 도달하기 오랜 step이 걸릴 수 있다는 점이 있다.

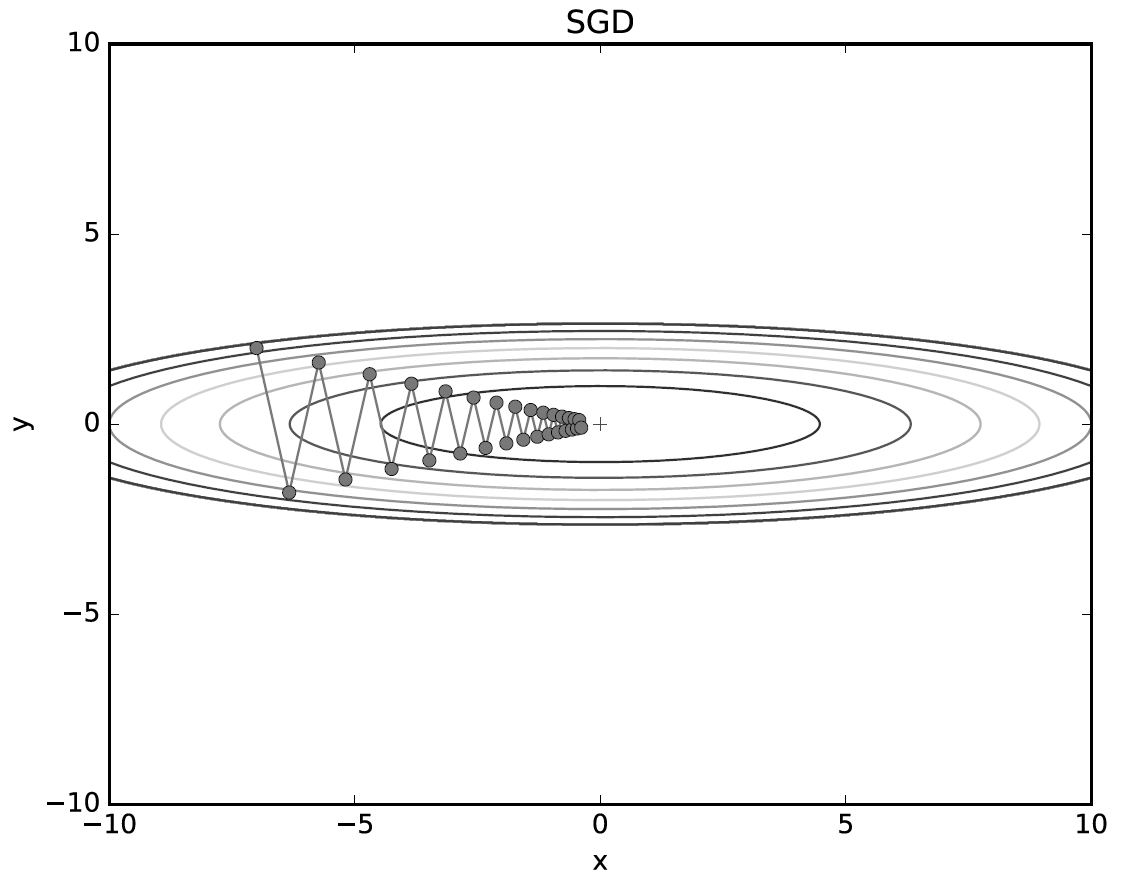
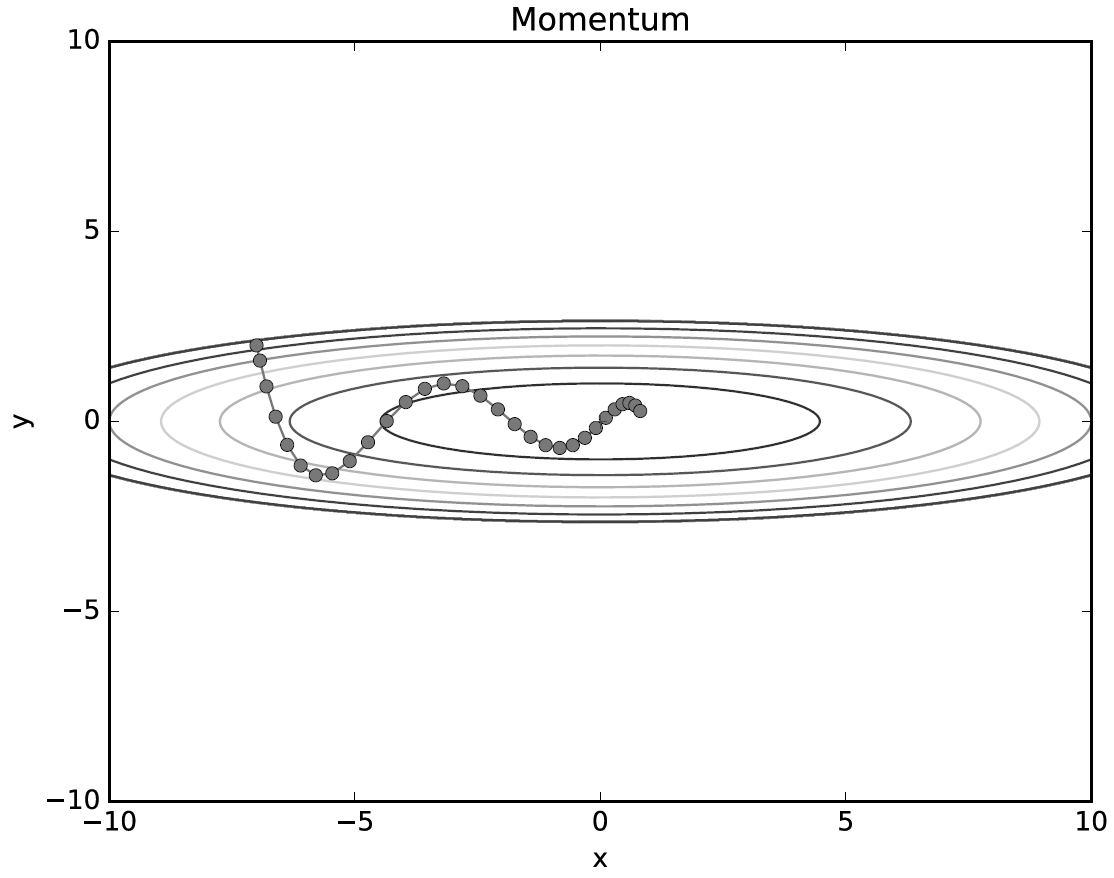
Momentum(모멘텀)

위의 안장점에 도달하면 더 이상 학습이 진행되지 않는 SGD의 단점을 보완한 Optimizer이다.

v \gets \alpha v - \eta \frac{\partial L}{\partial W} \\ W \gets W + v

위의 내용과 동일하지만 알파와 v가 추가되었다. 모멘텀은 운동량을 의미한다. SGD만큼 현재 위치의 기울기에 크게 영향을 받지 않고, 원래 진행하던 방향으로 가려는 관성을 어느정도 가진다. 하지만 알파값에 따라 기울기가 줄어들면 전체 갱신값을 줄이는 방향으로 학습이 진행된다.