Universal Approximation Theorem

UAT란?

일단 위키백과에 따르면 UAT는 다음과 같이 나와있다.

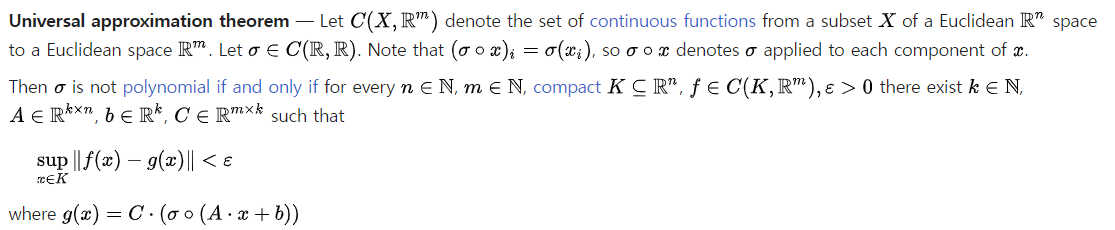
이산한 수식들이 여러가지 있다. 그러나 UAT가 말하고자 하는 것은 간단하고 또 네트워크(딥러닝)에는 어떻게 적용되는지는 저러한 수식과는 관련이 없다고 느껴진다.
일단 UAT의 정의를 해석해보자면
정의역 X(저 위의 설명에서는 n-dim인 real num)에서 m-dim(real num)으로의 실수를 치역으로 갖는 연속적인 함수들의 집합이 존재한다고 하자. 그러면 R->R인 연속적인 함수들의 집합에 시그마가 존재한다고 하자.(여기서 시그마는 딥러닝에서 활성화 함수임) 시그마는 nonpolynomial이고,
n,m은 자연수고, K는 n-dim 실수에 속하는 작은 범위(이 범위에서 근사를 할 예정), ε는 아주 작은 양수 라고 하자. 그러면, 근사시키려는 범위인 K내에서 실제함수 f와 선형결합으로 이루어진 함수인 근사함수 g의 오차가 ε보다 작게 근사할 수 있다는 내용이다.

실제 네트워크에 적용해보면 결과적으로 1층 이상의 hidden layer가 있다면 어떠한 함수든 딥러닝을 통해서(epoch가 무한으로 간다면 이론적으로) 원하는 오차보다 작게 근사할 수 있다는 것이다.

예제

1차원->1차원

이론적으로 학습이 무한적이라면 완벽히 근사한 함수를 찾을 수 있지만, 10000번만 학습을 해도 유의미한 결과를 눈으로 확인할 수 있었다.

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt


# 임의의 연속함수 설정 (R->R)
def true_function(x):
    return torch.sin(x) + torch.cos(2 * x)

# 훈련 데이터 생성
x_train = torch.linspace(0, 2 * np.pi, 100)
y_train = true_function(x_train)

# 신경망 모델 정의
class UniversalApproximator(nn.Module):
    def __init__(self):
        super(UniversalApproximator, self).__init__()
        self.hidden = nn.Linear(1, 50)  # 은닉 레이어
        self.output = nn.Linear(50, 1)  # 출력 레이어

    def forward(self, x):
        x = torch.relu(self.hidden(x))  # ReLU 활성화 함수
        x = self.output(x)
        return x

# 모델 생성
model = UniversalApproximator()

# Loss function & Optimizer
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)

# Train
num_epochs = 10000
for epoch in range(num_epochs):
    optimizer.zero_grad()
    outputs = model(x_train.unsqueeze(1))
    loss = criterion(outputs, y_train.unsqueeze(1))
    loss.backward()
    optimizer.step()

# Visualization
x_test = torch.linspace(0, 2 * np.pi, 1000)
with torch.no_grad():
    y_pred = model(x_test.unsqueeze(1))

plt.figure(figsize=(10, 6))
plt.plot(x_train, y_train, label='True Function')
plt.plot(x_test, y_pred, label='Approximation')
plt.legend()
plt.title('Universal Approximation with PyTorch')
plt.show()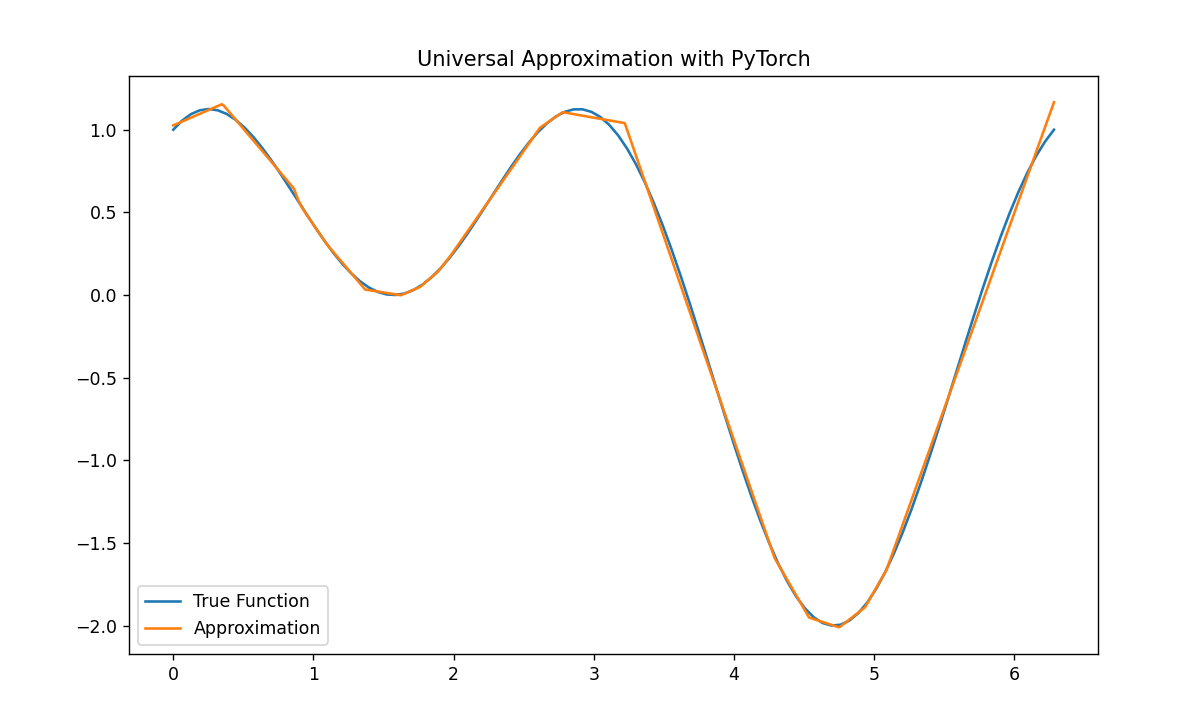

예제2

1차원 -> 3차원으로 코드를 진행해보려고 했으나 노트북인 관계로 Ram용량이 달려서 실행할 수 없었음..

용례

UAT는 네트워크를 구성하는 근본적인 이론이다. 그러므로 네트워크를 구성해서 푸는 대부분의 문제에 이용할 수 있고 쓰인다고 생각하면 된다.

• 회귀
• 분류
• Time Series
• Image Process
• NLP
• 강화학습
  등등 여러가지에 사용된다.

의의

UAT를 이해하는것은 코드를 작성하는 데에는 도움이 되지 않는다고 생각한다. 하지만 코들르 작성하면서 항상 들었던 의문이 "이렇게 코드를 작성하면 답을 어떠한 방식으로 찾을 수 있는거지?"라는 의문이 들었다. 결국 활성화 함수를 제외하면 모든 layer들은 linear combination의 형태를 가지고 있고, 함수를 근사하기는 힘들 것 같다라는 생각이었다. 하지만 이를 공부하고 나서 수학적으로 activation function의 존재와 함께라면 모든 함수를 근사할 수 있다고 하니 왜 layer를 많이 쌓는것이 좋고 어떤식으로 네트워크를 구성하면 좋을지에 대해 한번 더 생각할 수 있는 기회가 된 것 같다.