[Data Structure / Algorithms] Cycle Detection in Graphs (사이클 판별)

전성훈·2023년 11월 15일

Algorithms datastructure swift

Data Structure-Algorithm

목록 보기

31/35

주제: 그래프 사이클 판별 방법

무방향 그래프에서 사이클 판별 (Union - Find, DFS)

무방향 그래프에서 사이클을 판별하는 것은 그래프 이론에서 중요한 문제 중 하나입니다. 사이클 판별은 그래프 순환 구조를 가지고 있는지 여부를 확인하는 데 사용됩니다. 무방향 그래프에서 사이클을 판별하는 두 가지 주요 방법은 Disjoint Set과 DFS 입니다.
무방향 그래프에서 사이클을 판별하는 것은 여러 알고리즘과 응용 분야에서 중요합니다. 예를 들면, 최소 신장 트리(Minimum Spanning Tree, MST)를 찾는 크루스칼 알고리즘에서 사이클을 확인하여 불필요한 간선을 추가하지 않도록 할수있습니다.

UnionFind를 활용한 무방향 그래프 사이클 판별

Disjoint Set을 활용한 무방향 그래프 사이클 판별의 key point는 union 연산에 있습니다. union 연산을 통해 그래프에서의 간선으로 표현될 수 있기 때문입니다.

수행 방법

그래프의 각 노드를 서로소 집합의 원소로 간주하고, 각 노드를 자신만을 포함하는 집합으로 초기화합니다.
각 간선을 확인하며 두 노드의 루트 노드를 확인합니다.
1. 루트 노드가 서로 다르다면 두 노드에 대하여 union 연산을 수행합니다.
2. 루트 노드가 서로 같다면 cycle이 발생한 것 입니다.
그래프에 포함되어 있는 모든 간선에 대하여 위 과정을 반복합니다.

import Foundation

// Disjoint Set을 활용한 무방향 그래프 사이클 찾기
struct DisjointSet {
    var parent: [Int]
    var rank: [Int]
    
    init(count: Int) {
        parent = Array(0..<count)
        rank = Array(repeating: 0, count: count)
    }
    
    mutating func find(_ x: Int) -> Int {
        if parent[x] != x {
            parent[x] = find(parent[x])
        }
        
        return parent[x]
    }
    
    mutating func union(_ x: Int, _ y: Int) {
        let xRoot = find(x)
        let yRoot = find(y)
        
        if xRoot != yRoot {
            if rank[xRoot] < rank[yRoot] {
                parent[xRoot] = yRoot
            } else if rank[xRoot] > rank[yRoot] {
                parent[yRoot] = xRoot
            } else {
                parent[yRoot] = xRoot
                rank[xRoot] += 1
            }
        }
    }
}

func hasCycle(edges: [(Int, Int)], nodeCount: Int) -> Bool {
    var disjointSet = DisjointSet(count: nodeCount)
    
    for edge in edges {
        let xRoot = disjointSet.find(edge.0)
        let yRoot = disjointSet.find(edge.1)
        
        if xRoot == yRoot {
            return true
        }
        
        disjointSet.union(edge.0, edge.1)
    }
    
    return false
}


let test = hasCycle(edges: [(0,1), (0,2), (1,2)], nodeCount: 3)

true

DFS를 활용한 무방향 그래프 사이클 판별

그래프의 모든 노드에 대해서 DFS를 수행합니다.
DFS를 진행하면서, 이미 방문한 노드를 다시 만날 경우 사이클이 존재하는 것으로 판단합니다.
여기서 key point는 부모 노드를 다시 방문하는 것은 사이클로 간주하지 않는다는 것 입니다. 즉, 현재 노드의 인접 노드를 방문할 때, 해당 인접 노드가 이전에 방문한 노드이면서 현재 노드의 부모 노드가 아니라면 사이클이 있는 것으로 판단합니다.
DFS 탐색 중, 현재 노드에서 인접한 노드로 이동할 때, 인접 노드가 이전에 방문한 노드라면 사이클이 존재할 수 있습니다. 하지만, 인접 노드가 현재 노드로 이동하기 전에 방문했던 노드 즉, 부모 노드일 경우는 예외 입니다.
부모 노드란 DFS에서 현재 노드로 진입하기 바로 전에 탐색했던 노드를 말합니다. 무방향 그래프에서는 양방향 연결이 가능하므로, 부모 노드로 다시 돌아가는 것이 자연스러운 과정이기 때문입니다.
이를 사이클로 간주하지 않는 것은, 부모 노드로의 이동이 사이클이 아닌 탐색 경로의 일부라는 것을 인식하기 위함입니다.

func isCycle(
    _ graph: [[Int]],
    _ v: Int,
    _ visited: inout [Bool],
    _ parent: Int
) -> Bool {
	// visited 처리 
    visited[v] = true

	// 2차원 배열 요소 접근 
    for i in graph[v] {
	    // 해당 요소에 대해서 접근이 안 되어 있을 때 발동
        if !visited[i] {
	        // 해당 함수 재귀처리하면서 부모 노드로 현재 노드를 부여
            if isCycle(graph, i, &visited, v) {
                return true
            }
            // 방문했지만, i가 parent일때는 무시 
        } else if i != parent {
            return true
        }
    }
    return false
}

func checkCycle(_ graph: [[Int]], _ n: Int) -> Bool {
    var visited = [Bool](repeating: false, count: n)
    
    for v in 0..<n {
        if !visited[v] {
	        // 사이클이 있는지 확인,
	        // 최초값을 최소값의 -1 값을 부여
            if isCycle(graph, v, &visited, -1) {
                return true
            }
        }
    }
    
    return false
}


print(checkCycle([[0,1,1], [1,0,1], [1,1,0]], 3))

무방향 그래프 사용

서로소 집합

서로소 집합은 주로 무방향 그래프에서 사이클을 판별하는 데 사용됩니다. 이 방법은 무방향 그래프의 연결 요소를 관리하고, 두 노드가 같은 집합에 속하는지 빠르게 확인할 수 있기 때문에 크루스칼 알고리즘과 같은 최소 신장 트리 문제에서 유용합니다.
서로소 집합은 각 간선에 대해 두 노드의 루트를 찾고, 두 루트가 다르면 합치는 연산을 수행합니다. 경로 압축과 랭크 최적화를 사용하면 거의 $O(1)$ 에 가까운 시간에 연산을 수행할 수 있습니다.
따라서 전체 시간 복잡도는 $O(E)$ (간선)에 가깝습니다.

DFS

DFS는 방향 그래프에서 사이클을 찾는 데 유용합니다. 그럼에도 불구하고 무방향 그래프에서 DFS를 사용할 수 있지만, 부모 노드와의 구별을 명확하게 해야 합니다.
DFS는 그래프의 모든 노드와 간선을 한 번씩 방문하므로 시간 복잡도는 $O(V+E)$ 입니다.

결론

일반적으로, 무방향 그래프의 사이클 판별에서 서로소 집합이 더 간결하고 효율적인 경우가 많습니다. 하지만 그래프의 특성이나 문제의 요구 사항에 따라 DFS를 사용할 수 도 있습니다.

방향 그래프에서 사이클 판별 (DFS)

방향 그래프에서 사이클을 판별하는 일반적인 방법은 깊이 우선 탐색(DFS)을 사용하는 것입니다. 이 방법은 그래프의 노드를 탐색하면서 탐색 경로에 이미 방문한 노드가 나타나면 사이클이 존재한다고 판단합니다.
방향 그래프에서 사이클의 존재 여부는 다양한 알고리즘과 시스템에서 중요합니다. 예를 들면, 의존성 해결, 스케줄링, 데드락 감지 등 많은 CS 분야에서 사이클의 존재 여부를 확인해야 할 때 필요합니다.

수행 방법

각 노드의 방문 상태를 확인하기 위한 두 가지 배열을 준비합니다.
1. 일반적인 방문 상태인 Visited를 표시합니다.
2. 현재 DFS 경로 상의 노드를 Recursive Stack 를 사용해서 표시합니다.
DFS를 수행합니다.
DFS 수행 중에 현재 DFS 경로 상의 노드 (recStack에 있는 노드)를 다시 만나면 사이클이 존재한다고 판단합니다. 즉, recStack 배열에 이미 표시된 노드를 방문하면 사이클이 존재하는 것 입니다.
각 노드에 대한 DFS가 완료되면 해당 노드를 recStack에서 제거합니다.

Recursive Stack

recStack은 현재 DFS 탐색 경로에 있는 노드들을 추적합니다. DFS가 특정 노드를 방문할 때, 해당 노드는 recStack 에 추가됩니다.
recStack에 있는 노드를 다시 방문하면 사이클이 있는 것으로 간주합니다.

사용 방법

DFS가 노드를 처음 방문할 때, 해당 노드는 visited 배열에 기록되고 recStack에 추가됩니다.
DFS가 인접 노드를 탐색할 때, 만약 해당 인접 노드가 이미 visited되었고, recStack에도 존재한다면, 사이클이라고 판단합니다.
노드의 DFS 탐색이 끝나고 더 이상 탐색할 인접 노드가 없을 때, 해당 노드는 recStack에서 제거됩니다.

Recursive Stack의 존재 이유

Visited만으로 circle을 판단했을 때
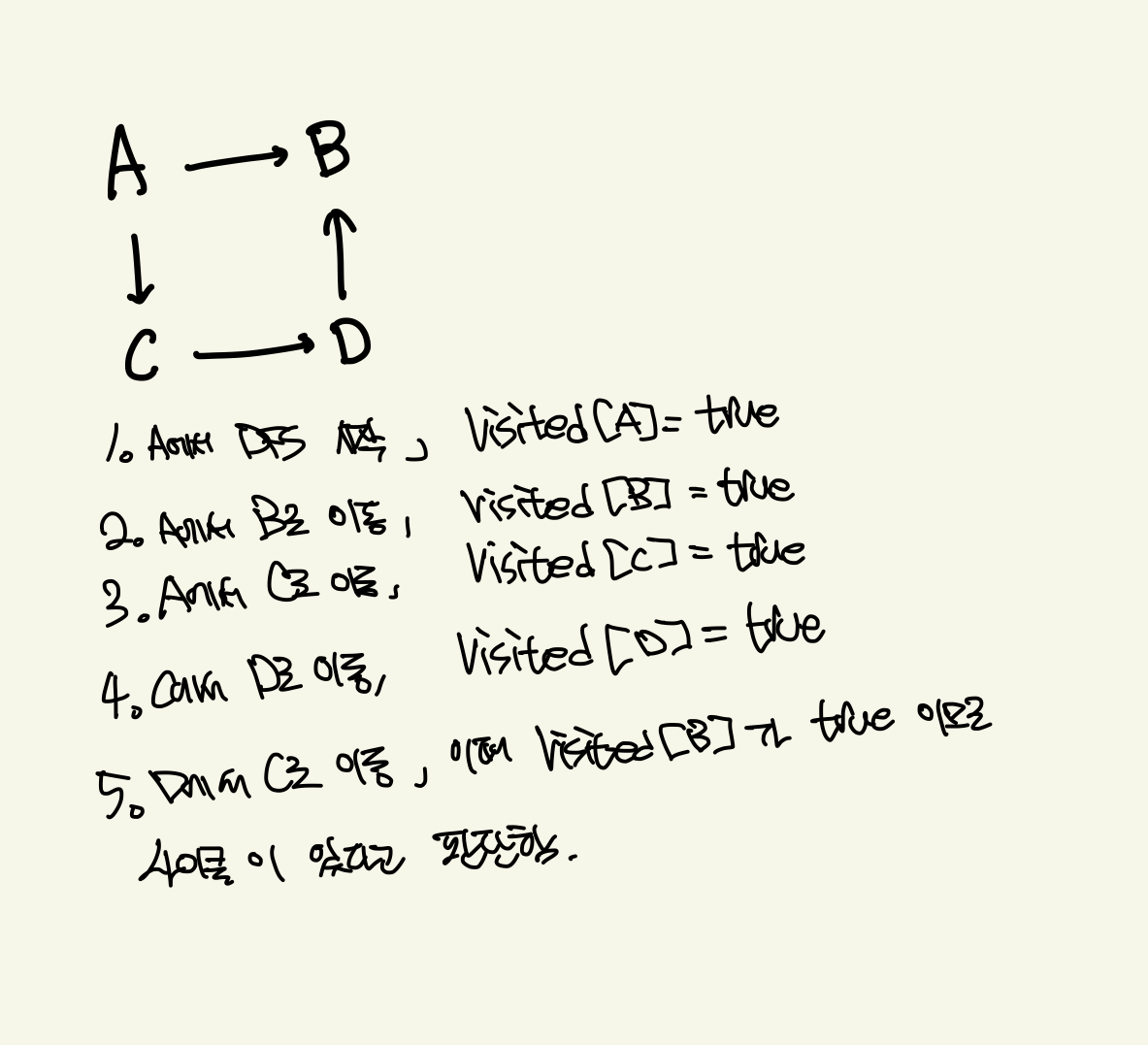
recStack을 활용하여 circle을 판단했을 때

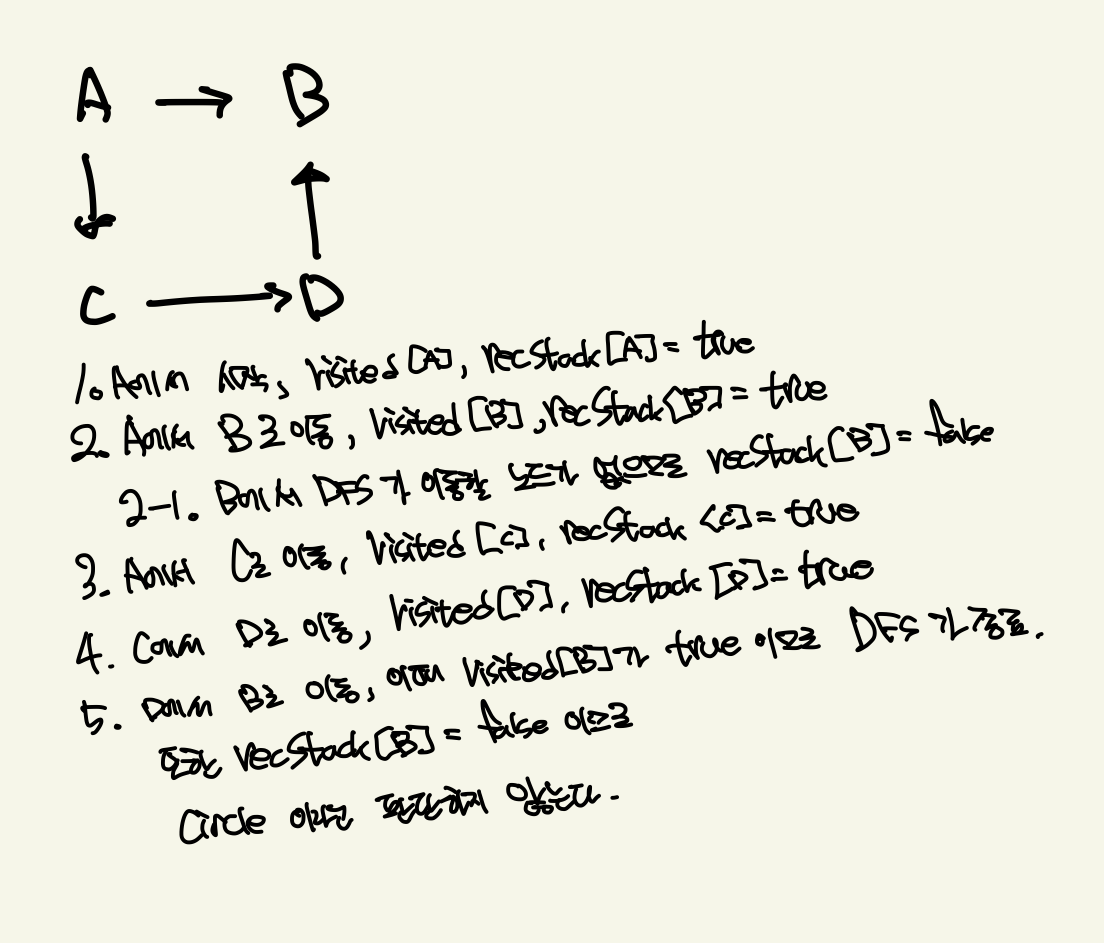
구현

// 인접 리스트 방식 
func isCycle(
    _ graph: inout [[Int]],
    _ v: Int,
    _ visited: inout [Bool],
    _ recStack: inout [Bool]
) -> Bool {
    if !visited[v] {
        visited[v] = true
        recStack[v] = true
        
        for neighbor in graph[v] {
            if !visited[neighbor] && isCycle(&graph, neighbor, &visited, &recStack) {
                return true
            } else if recStack[neighbor] {
                return true
            }
        }
    }
    recStack[v] = false
    
    return false
}



func dfs(_ graph: inout [[Int]], _ n: Int) -> Bool {
    var visited = [Bool](repeating: false, count: n)
    var recStack = [Bool](repeating: false, count: n)
    
    for v in 0..<n {
        if isCycle(&graph, v, &visited, &recStack) {
            return true
        }
    }
    
    return false
}

var graph = [[1,2],[],[3],[1]]
let n = 4 //
let hasCycle = dfs(&graph, n)

print(hasCycle ? "YES" : "NO")

NO

예제

무방향 그래프에서 사이클 판별 - 백준 사이클 게임 20040 (골드 4)

문제

사이클 게임은 두 명의 플레이어가 차례대로 돌아가며 진행하는 게임으로, 선 플레이어가 홀수 번째 차례를, 후 플레이어가 짝수 번째 차례를 진행한다. 게임 시작 시 0 부터 n − 1 까지 고유한 번호가 부여된 평면 상의 점 n 개가 주어지며, 이 중 어느 세 점도 일직선 위에 놓이지 않는다. 매 차례 마다 플레이어는 두 점을 선택해서 이를 연결하는 선분을 긋는데, 이전에 그린 선분을 다시 그을 수는 없지만 이미 그린 다른 선분과 교차하는 것은 가능하다. 게임을 진행하다가 처음으로 사이클을 완성하는 순간 게임이 종료된다. 사이클 C는 플레이어가 그린 선분들의 부분집합으로, 다음 조건을 만족한다.

C에 속한 임의의 선분의 한 끝점에서 출발하여 모든 선분을 한 번씩만 지나서 출발점으로 되돌아올 수 있다.
문제는 선분을 여러 개 그리다 보면 사이클이 완성 되었는지의 여부를 판단하기 어려워 이미 사이클이 완성되었음에도 불구하고 게임을 계속 진행하게 될 수 있다는 것이다. 이 문제를 해결하기 위해서 게임의 진행 상황이 주어지면 몇 번째 차례에서 사이클이 완성되었는지, 혹은 아직 게임이 진행 중인지를 판단하는 프로그램을 작성하려 한다.
입력으로 점의 개수 n 과 m 번째 차례까지의 게임 진행 상황이 주어지면 사이클이 완성 되었는지를 판단하고, 완성되었다면 몇 번째 차례에서 처음으로 사이클이 완성된 것인지를 출력하는 프로그램을 작성하시오.

입력

입력은 표준입력을 사용한다. 입력의 첫 번째 줄에는 점의 개수를 나타내는 정수 3 ≤ n ≤ 500,000 과 진행된 차례의 수를 나타내는 정수 3 ≤ m ≤ 1,000,000 이 주어진다. 게임에서 사용하는 n 개의 점에는 0 부터 n − 1 까지 고유한 번호가 부여되어 있으며, 이 중 어느 세 점도 일직선 위에 놓이지 않는다. 이어지는 m 개의 입력 줄에는 각각 i 번째 차례에 해당 플레이어가 선택한 두 점의 번호가 주어진다 (1 ≤ i ≤ m).

출력

출력은 표준출력을 사용한다. 입력으로 주어진 케이스에 대해, m 번째 차례까지 게임을 진행한 상황에서 이미 게임이 종료되었다면 사이클이 처음으로 만들어진 차례의 번호를 양의 정수로 출력하고, m 번의 차례를 모두 처리한 이후에도 종료되지 않았다면 0을 출력한다.

예제 입력 1

예제 출력 1

예제 입력 2

예제 출력 2

풀이

최초 Swift를 활용해서 무방향 사이클 판별 알고리즘인, Union - find를 사용했으나 swift에서 readLine의 속도가 너무 느려 시간초과가 되었다. 그러므로 python으로 문제를 해결했다.
해당 문제는 그래프에서 서로소 집합을 나누면서 사이클이 있으면 그 결과 값을 return하고 없으면 0을 return 해주면 된다.

import sys
input = sys.stdin.readline

class DisjointSet: 
	def __init__(self, count):
		self.parent = list(range(count))
		self.rank = [0] * count 
	
	def find(self, x):
		if self.parent[x] != x: 
			self.parent[x] = self.find(self.parent[x])
		return self.parent[x]
	
	def union(self, x, y):
		x_root = self.find(x)
		y_root = self.find(y)
		
		if x_root != y_root:
			if self.rank[x_root] < self.rank[y_root]:
				self.parent[x_root] = y_root
			elif self.rank[x_root] > self.rank[y_root]:
				self.parent[y_root] = x_root
			else: 
				self.parent[y_root] = x_root
				self.rank[x_root] += 1 

def has_cycle(edge, disjoint_set): 
	x_root = disjoint_set.find(edge[0])
	y_root = disjoint_set.find(edge[1])
	
	if x_root == y_root: 
		return true
	
	disjoint_set.union(edge[0], edge[1])
	return false 

def start(N,M): 
	disjoint_set = DisjointSet(N)
	result = 0
	
	for i in range(M):
		a, b = map(int, input().split())
		result = i + 1
		
		if has_cycle((a,b), disjoint_set):
			return result 
	return 0

N, M = map(int, input().split())

print(start(N, M))

방향 그래프에서 사이클 판별 - 백준 텀 프로젝트 9466 (골드 3)

문제

이번 가을학기에 '문제 해결' 강의를 신청한 학생들은 텀 프로젝트를 수행해야 한다. 프로젝트 팀원 수에는 제한이 없다. 심지어 모든 학생들이 동일한 팀의 팀원인 경우와 같이 한 팀만 있을 수도 있다. 프로젝트 팀을 구성하기 위해, 모든 학생들은 프로젝트를 함께하고 싶은 학생을 선택해야 한다. (단, 단 한 명만 선택할 수 있다.) 혼자 하고 싶어하는 학생은 자기 자신을 선택하는 것도 가능하다.
학생들이(s1, s2, ..., sr)이라 할 때, r=1이고 s1이 s1을 선택하는 경우나, s1이 s2를 선택하고, s2가 s3를 선택하고,..., sr-1이 sr을 선택하고, sr이 s1을 선택하는 경우에만 한 팀이 될 수 있다.
예를 들어, 한 반에 7명의 학생이 있다고 하자. 학생들을 1번부터 7번으로 표현할 때, 선택의 결과는 다음과 같다.

1	2	3	4	5	6	7
3	1	3	7	3	4	6

위의 결과를 통해 (3)과 (4, 7, 6)이 팀을 이룰 수 있다. 1, 2, 5는 어느 팀에도 속하지 않는다.
주어진 선택의 결과를 보고 어느 프로젝트 팀에도 속하지 않는 학생들의 수를 계산하는 프로그램을 작성하라.

입력

첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫 줄에는 학생의 수가 정수 n (2 ≤ n ≤ 100,000)으로 주어진다. 각 테스트 케이스의 둘째 줄에는 선택된 학생들의 번호가 주어진다. (모든 학생들은 1부터 n까지 번호가 부여된다.)

출력

각 테스트 케이스마다 한 줄에 출력하고, 각 줄에는 프로젝트 팀에 속하지 못한 학생들의 수를 나타내면 된다.

예제 입력 1

2
7
3 1 3 7 3 4 6
8
1 2 3 4 5 6 7 8

예제 출력 1

3
0

풀이

프로젝트 팀에 속하지 못한 학생들의 수를 출력하면된다. 이때 최초 count를 0으로 잡고 해당 학생이 사이클을 돌게 되었을 때 count를 추가하는 방식으로 해서 해당 count를 총 학생 수를 뺀 결과 값을 답으로 제출한다.
사이클을 확인하기 위해 visited를 확인하기 위한 배열 뿐만 아니라 사이클 확인 전용 배열(recStack)도 만들어줘야 한다.
해당 배열은 if !visited[n] 를 하고 else if !recStack[n] 분기에서 방문을 안했을 때 count를 진행해주고, dfs가 종료되는 시점에서 recStack을 true처리 해주면된다.
즉, key point는 visited는 dfs를 시작할때 방문처리, recStack은 모든 조건문 (내부 재귀 함수)가 종료될 때 방문처리를 해주면 된다.

import Foundation

let testCase = Int(readLine()!)!
var results = [Int]()

for _ in 0..<testCase {
	let r = Int(readLine()!)!
	
	let choices = [0] + readLine()!.split(separator: " ").map { Int($0)! }
	
	var visited = Array(repeating: false, count: r + 1)
	var recSatck = Array(repeating: false, count: r + 1)
	var count = 0
	
	func dfs(start: Int) {
		visited[start] = true
	      
	    var n = choices[start]
	    
	    if !visited[n] {
		dfs(start: n)
	    // 방문했고 해당 사이클이 아직 종료되지 않았다면 해당 조건 활성화
	    } else if !recSatck[n] {
		// 해당 사이클에서 시작점이 맞을때까지 시작점으로 이동하는 반복문
		    while n != start {
		        count += 1
		        n = choices[n]
		    }
		    // 해당 사이클이 시작점과 같다면 count만 하고 해당 사이클 종료
		    count += 1
		}
	    // 해당 노드에서 dfs가 종료될 때 recStack에 사이클 종료를 알림을 알린다.
		recSatck[start] = true
	}
	
	for i in 1...r {
		if !visited[i] {
	      dfs(start: i)
	    }
	  }
	  
	results.append(r - count)
}

results.forEach {
  print($0)
}

3 -> 3 일 때
- DFS(3): S = 3, V3 = true, N = 3이다. 이때 visted는 true이니 해당 분기는 넘어가며, 아직 사이클이 종료되지 않아서 else if문이 실행된다. 여기서 n == start이므로 count가 증가된다.
- 그 후 모든 조건문이 실행이 끝나면 recStack[start]이 true처리되고 해당 사이클이 종료된다.
4 ->7, 7 -> 6, 6 -> 4 일때
1. DFS(4): S = 4, n = 7이 되고 7은 방문하지 않았으므로 dfs(7)이 실행된다.
2. DFS(7): S = 7, n = 6이 되고 6은 방문하지 않았으므로 dfs(6)이 실행된다.
3. DFS(6): S = 6, n = 7이 되고 7은 방문했으므로 else if문이 실행된다.
4. 최초 n = 7, S = 6이므로 while문이 실행된다. while문은 7 -> 6 두 번 실행되며 n == s가 같게 될때 while문이 종료된다.
5. n == s 같을때 아래 count만 +=1 되는 것이 실행되며 총 3의 count가 증가된다.
6. 이 후 DFS(6)이 종료되면서 recStack[6] = true가 된다.
7. 차례로 DFS(7), DFS(4)가 종료되면서 recStack[7], [4] = true가 되며 한 사이클이 종료된다.

플러스 문제 - 백준 피리 부는 사나이 16724 (골드 3)

문제

피리 부는 사나이 성우는 오늘도 피리를 분다.
성우가 피리를 불 때면 영과일 회원들은 자기도 모르게 성우가 정해놓은 방향대로 움직이기 시작한다. 성우가 정해놓은 방향은 총 4가지로 U, D, L, R이고 각각 위, 아래, 왼쪽, 오른쪽으로 이동하게 한다.
이를 지켜보던 재훈이는 더 이상 움직이기 힘들어하는 영과일 회원들을 지키기 위해 특정 지점에 ‘SAFE ZONE’ 이라는 최첨단 방음 시설을 만들어 회원들이 성우의 피리 소리를 듣지 못하게 하려고 한다. 하지만 예산이 넉넉하지 않은 재훈이는 성우가 설정해 놓은 방향을 분석해서 최소 개수의 ‘SAFE ZONE’을 만들려 한다.
성우가 설정한 방향 지도가 주어졌을 때 재훈이를 도와서 영과일 회원들이 지도 어느 구역에 있더라도 성우가 피리를 불 때 ‘SAFE ZONE’에 들어갈 수 있게 하는 ‘SAFE ZONE’의 최소 개수를 출력하는 프로그램을 작성하시오.

입력

첫 번째 줄에 지도의 행의 수를 나타내는 N(1 ≤ N ≤ 1,000)과 지도의 열의 수를 나타내는 M(1 ≤ M ≤ 1,000)이 주어진다.
두 번째 줄부터 N개의 줄에 지도의 정보를 나타내는 길이가 M인 문자열이 주어진다.
지도 밖으로 나가는 방향의 입력은 주어지지 않는다.

출력

첫 번째 줄에 ‘SAFE ZONE’의 최소 개수를 출력한다.

예제 입력 1

3 4
DLLL
DRLU
RRRU

예제 출력 1

다음과 같이 'SAFE ZONE'을 만들면 영과일 회원들이 지도 어느 구역에 있더라도 'SAFE ZONE'에 들어갈 수 있다.

풀이

최초 그림과 문제를 보자마자 단순 사이클 수만 파악하면 될 줄알았다. 그래서 해당 그래프를 DFS를 수행하면서 사이클 수를 파악하면서 문제를 해결하려 했으나 계속해서 실패했었다.
그러다가 여러개의 사이클이 겹칠 수 있다는 것을 깨닫게되었고 해당 문제는 사이클 갯수를 파악하는 것이 아니라 Union 개수를 파악하는 것이라는걸 알게되었다.
해당 그래프에 대해서 union - find를 수행하면서 해당 결과에 대해 Set 자료구조에 더해준다.
마지막으로 Set 자료구조의 개수를 출력하면 된다.

import Foundation

struct DisjointSet {
    var parent: [Int]
    var rank: [Int]

    init(count: Int) {
        parent = Array(0..<count)
        rank = Array(repeating: 0, count: count)
    }

    mutating func find(_ x: Int) -> Int {
        if parent[x] != x {
            parent[x] = find(parent[x])
        }
        return parent[x]
    }

    mutating func union(_ x: Int, _ y: Int) {
        let xRoot = find(x)
        let yRoot = find(y)
        
        if xRoot != yRoot {
            if rank[xRoot] < rank[yRoot] {
                parent[xRoot] = yRoot
            } else if rank[xRoot] > rank[yRoot] {
                parent[yRoot] = xRoot
            } else {
                parent[yRoot] = xRoot
                rank[xRoot] += 1
            }
        }
    }
}

let testCase = readLine()!.components(separatedBy: " ").map { Int($0)! }
let N = testCase[0]
let M = testCase[1]

var graph = [[String]]()
for _ in 0..<N {
    graph.append(readLine()!.map { String($0) })
}

var disjointSet = DisjointSet(count: N * M)

let dx = [-1, 1, 0, 0]
let dy = [0, 0, -1, 1]
let directions: [String: Int] = ["U": 0, "D": 1, "L": 2, "R": 3]

for i in 0..<N {
    for j in 0..<M {
        let direction = directions[graph[i][j]]!
        let nx = i + dx[direction]
        let ny = j + dy[direction]

        if nx >= 0 && nx < N && ny >= 0 && ny < M {
	        // 해당 위치에서 주어진 값에 따라 이동 후 해당 값과 이동 후 값에 대해서 union을 해준다. 
	        // 2차원 배열을 1차원으로 플릿화 
            let current = i * M + j
            let next = nx * M + ny
            disjointSet.union(current, next)
        }
    }
}

var safeZones = Set<Int>()
for i in 0..<N {
    for j in 0..<M {
	    // 2차원 배열을 1차원으로 플릿 후 
        let index = i * M + j
        // find 메서드를 활용해서 부모 노드를 safeZone에 넣어준다. 
        safeZones.insert(disjointSet.find(index))
    }
}

print(safeZones.count)

하지만 위 방법처럼 복잡하게 Disjoint set를 사용하지 않고도 문제를 해결할 수 있다. 방법은 Visited을 방문 전, 방문 중, 방문 후 로 나누고 해당 그래프를 DFS를 수행하면서 방문 전을 탐색 할땐 정상적인 DFS, 방문 중을 탐색 할땐 count ++, 방문 후를 탐색하면 union이 된것으로 판단하고 dfs를 종료한다.

import Foundation

let testCase = readLine()!.components(separatedBy: " ").map { Int($0)! }

let N = testCase[0]
let M = testCase[1]

var graph = [[String]](repeating: [String](), count: N)

// Visted을 3단계로 나눠서 해결
// 0 -> 방문 x
// 1 -> 방문 중
// 2 -> 방문 끝
// 즉, 방문 중인걸 다시 방문할 경우 circle이 생김
var visited = [[Int]](repeating: [Int](repeating: 0, count: M), count: N)

for i in 0..<N {
    let line = readLine()!.map { String($0) }
    graph[i] = line
}


let dx = [-1,1,0,0]
let dy = [0,0,-1,1]

let directions: [String: Int] = ["U": 0, "D": 1, "L": 2, "R": 3]

var result = 0

func dfs(x: Int, y: Int) {
    // 방문 처리
    visited[x][y] = 1

    let direction = directions[graph[x][y]]!
    let nx = x + dx[direction]
    let ny = y + dy[direction]

    if nx >= 0 && nx < N && ny >= 0 && ny < M {
        if visited[nx][ny] == 1 {
            result += 1
        } else if visited[nx][ny] == 0 {
            dfs(x: nx, y: ny)
        }
    }

    visited[x][y] = 2
}

for i in 0..<N {
    for j in 0..<M {
        if visited[i][j] == 0 {
            dfs(x: i, y: j)
        }
    }
}

print(result)

결론은 union find라고해서 무조건 무방향만 사용하는것이 아니고, DFS라고 해서 무조건 방향만 사용하는 것이 아니다.
문제의 해결방법은 다양하다.
마지막으로 문제에 숨어있는 TestCase에 대해서 잘 찾아내는 능력을 키워야될 필요성이 있다.

출처(참고문헌)

이코테 - 나동빈
https://www.geeksforgeeks.org/detect-cycle-in-a-graph/
https://yuminlee2.medium.com/detect-cycle-in-a-graph-4461b6000845
https://nicotina04.tistory.com/148
https://www.acmicpc.net/problem/20040
https://www.acmicpc.net/problem/9466
https://www.acmicpc.net/problem/16724

제가 학습한 내용을 요약하여 정리한 것입니다. 내용에 오류가 있을 수 있으며, 어떠한 피드백도 감사히 받겠습니다.

감사합니다.

전성훈

이전 포스트

[Data Structure / Algorithms] Disjoint-Set Structure (Union - Find Algorithms)

다음 포스트

[Data Structure / Algorithms] Cycle Detection in Graphs (사이클 판별)

Data Structure-Algorithm

주제: 그래프 사이클 판별 방법

무방향 그래프에서 사이클 판별 (Union - Find, DFS)

UnionFind를 활용한 무방향 그래프 사이클 판별

수행 방법

DFS를 활용한 무방향 그래프 사이클 판별

무방향 그래프 사용

서로소 집합

DFS

결론

방향 그래프에서 사이클 판별 (DFS)

수행 방법

Recursive Stack

사용 방법

Recursive Stack의 존재 이유

구현

예제

무방향 그래프에서 사이클 판별 - 백준 사이클 게임 20040 (골드 4)

문제

입력

출력

예제 입력 1

예제 출력 1

예제 입력 2

예제 출력 2

풀이

방향 그래프에서 사이클 판별 - 백준 텀 프로젝트 9466 (골드 3)

문제

입력

출력

예제 입력 1

예제 출력 1

풀이

플러스 문제 - 백준 피리 부는 사나이 16724 (골드 3)

문제

입력

출력

예제 입력 1

예제 출력 1

풀이

출처(참고문헌)

[Data Structure / Algorithms] Disjoint-Set Structure (Union - Find Algorithms)

[Data Structure / Algorithms] Methods for Finding a MST(Minimum Spannig Tree) - Kruskal & Prim

0개의 댓글