[Data Structure / Algorithms] Methods for Finding a MST(Minimum Spannig Tree) - Kruskal & Prim

주제: 크루스칼 & 프림 알고리즘을 사용해서 최소 신장 트리 찾는법

---

신장 트리(Spanning Tree)란

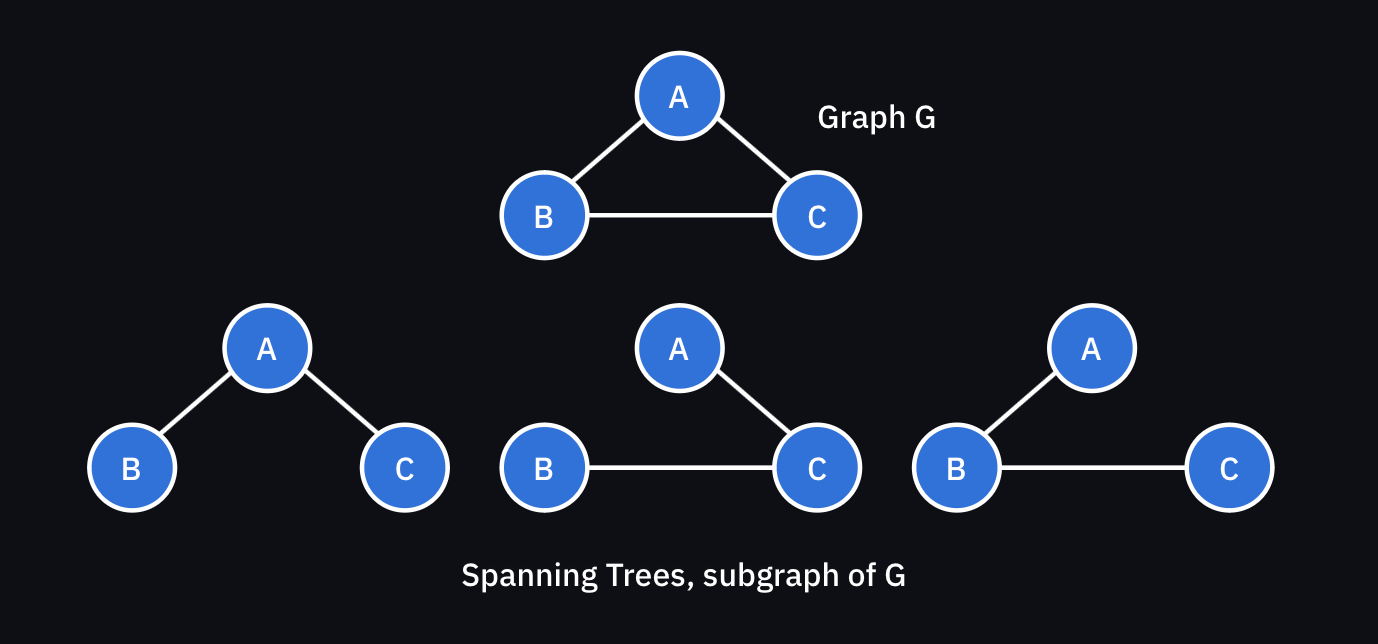
• 신장 트리는 Undirected 그래프에서 모든 정점을 포함하면서 최소한의 간선으로 연결되어 있는 그래프입니다.
• 이는 하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미합니다.
• 즉, 그래프에서 모든 노드를 포함하고 모든 노드가 서로 연결되어 있지만, 최소한의 간선만을 사용하여 구성된 트리를 말합니다.
• 특징으론 신장 트리는 그래프의 모든 노드를 포함하므로, 그래프의 있는 노드의 수가 N개라면 신장 트리는 정확히 N-1 개의 간선을 가집니다.
  

최소 신장 트리(Minimum Spanning Tree,MST)

• 최소 신장 트리는 그래프의 신장 트리 중에서 사용된 간선들의 가중치 합이 최소인 트리를 말합니다. 즉, 원래 그래프의 모든 노드를 포함하면서 간선의 가중치 합이 가장 작은 트리를 말합니다.
• 최소 신장 트리는 네트워크 설계, 클러스터 분석, 통신 네트워크 등 다양한 분야에서 최적화 문제를 해결하는 데 사용됩니다.
• 최소 신장 트리를 찾는 대표적인 알고리즘은 Prim, Kruskal 알고리즘이 있습니다.

  • Kruskal(크루스칼) Algorithm: 모든 간선을 가중치에 따라 오름차순으로 정렬한 후, 가장 가중치가 낮은 간선부터 선택하여 트리를 구성합니다. 이 과정에서 사이클이 형성되지 않도록 주의합니다.
  • Prim (프림) Algorithm: 한 노드에서 시작하여, 연결된 노드를 중 최소 가중치를 가진 간선을 선택하며 트리를 확장합니다.

• 최소 신장 트리는 그래프의 신장 트리 중 하나이면서, 이는 간선의 가중치 합이 최소인 것을 의미하기도 합니다.

크루스칼(Kruskal) 알고리즘

작동 원리

1. 그래프의 모든 간선을 가중치에 따라 오름차순으로 정렬합니다.
2. 정렬된 간선 목록을 순회하면서, 각 간선을 하나씩 선택합니다. 선택한 간선이 사이클을 발생하는지 확인합니다.
   2-1. 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킵니다.
   2-2. 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않습니다.
3. 모든 간선에 대하여 2번의 과정을 반복합니다.

• 크루스칼 알고리즘에서는 서로소 집합(Disjoint Set) 자료구조를 사용하여 두 노드가 같은 집합에 속하는지 판단합니다.

특징과 장점

• 크루스칼 알고리즘은 구현이 비교적 간단하며 이해하기 쉽습니다.
• 크루스칼 알고리즘은 가중치가 있는 연결된 무방향 그래프에서 활용됩니다.
• 크루스칼 알고리즘은 희소 그래프(간선의 수가 노드에 비해 상대적으로 적은 그래프)에서 특히 효율적입니다.
• 크루스칼 알고리즘은 주로 통신 네트워크, 전기 회로 설계, 도로망 설계 등 다양한 최적화 문제에 활용됩니다.

복잡도

• 크루스칼 알고리즘의 시간 복잡도는 주로 간선을 정렬하는 데 소요되는 시간에 의해 결정됩니다. 간선 정렬에는 O(ElogE)의 시간이 소요됩니다. E: 간선의 수
• 각 간선에 대해 find와 union 연산은 거의 상수 시간에 가깝게 수행될 수 있기 때문에 무시됩니다.
• 크루스칼 알고리즘의 공간 복잡도는 O(E + V) 입니다. 여기서 V는 노드의 수이며, 이는 서로소 집합과 간선 리스트를 저장하는데 필요한 공간입니다.

예시

구현

import Foundation

// 간선에 대한 정보를 담는 구조체
struct Edge {
    var node1: Int
    var node2: Int
    var weight: Int
}

// 서로소 집합 자료구조
struct DisjointSet {
    var parent: [Int]
    var rank: [Int]
    
    init(count: Int) {
        parent = Array(0...count)
        rank = Array(repeating: 0, count: count + 1)
    }
    
    mutating func find(_ node: Int) -> Int {
        if parent[node] != node {
            parent[node] = find(parent[node])
        }
        
        return parent[node]
    }
    
    mutating func union(_ node1: Int, _ node2: Int) {
        let root1 = find(node1)
        let root2 = find(node2)
        
        if root1 != root2 {
            if rank[root1] < rank[root2] {
                parent[root1] = root2
            } else if rank[root1] > rank[root2] {
                parent[root2] = root1
            } else {
                parent[root2] = root1
                rank[root1] += 1
            }
        }
    }
}

// 크루스칼 알고리즘 구현
func kruskal(edges: [Edge], nodeCount: Int) -> Int {
    var disjointSet = DisjointSet(count: nodeCount)
    // 가중치 오름차순으로 정렬
    let sortedEdges = edges.sorted { $0.weight < $1.weight}
    
    var totalWeight = 0
    for edge in sortedEdges {
	    // 두 노드에 대해서 부모 노드가 같다면 무시 
        if disjointSet.find(edge.node1) != disjointSet.find(edge.node2) {
            disjointSet.union(edge.node1, edge.node2)
            totalWeight += edge.weight
        }
    }
    
    return totalWeight
}

let nodeCount = 7

let edge1 = Edge(node1: 1, node2: 2, weight: 29)
let edge2 = Edge(node1: 1, node2: 5, weight: 75)
let edge3 = Edge(node1: 2, node2: 3, weight: 35)
let edge4 = Edge(node1: 2, node2: 6, weight: 34)
let edge5 = Edge(node1: 3, node2: 4, weight: 7)
let edge6 = Edge(node1: 4, node2: 6, weight: 23)
let edge7 = Edge(node1: 4, node2: 7, weight: 13)
let edge8 = Edge(node1: 5, node2: 6, weight: 53)
let edge9 = Edge(node1: 6, node2: 7, weight: 25)

let edges = [edge1, edge2, edge3, edge4, edge5, edge6, edge7, edge8, edge9]

kruskal(edges: edges, nodeCount: nodeCount)

159 

프림(Prim) 알고리즘

작동 원리

1. 그래프에서 임의의 노드를 선택합니다.
2. 선택한 노드에 인접한 간선들을 조사하며, 아직 신장 트리에 포함되지 않은 노드로 연결되는 가장 낮은 가중치의 간선을 찾습니다.
3. 해당 간선과 연결된 노드를 신장 트리에 추가합니다.
4. 모든 노드가 신장 트리에 포함될 때까지 위의 과정을 반복합니다.

• 프림 알고리즘은 우선순위 큐를 사용하여 다음에 추가할 간선을 효율적으로 선택합니다. 이는 각 단계에서 가능한 최소 가중치 간선을 빠르게 찾기 위함 입니다.

특징과 장점

• 프림 알고리즘은 MST를 구하기 위한 greedy 알고리즘 입니다.
• greedy 알고리즘이란 문제를 해결하기 위해 단계를 거치며, 모든 단계에서 최적의 경로를 찾는 알고리즘 입니다.
• 프림 알고리즘은 밀집 그래프(노드에 연결된 간선의 수가 많은 그래프)에서 특히 효율적입니다. 이는 각 단계에서 인접한 간선만을 고려하기 때문입니다.
• 프림 알고리즘은 구현이 비교적 간단하며, 이해하기 쉽습니다.
• 통신 네트워크, 전기 회로 설계, 도로망 구축 등에서 최소 비용으로 모든 노드를 연결하는 문제에서 최적화 문제에서 활용됩니다.
• 프림 알고리즘은 희소 그래프(간선이 상대적으로 적은 그래프)에서는 크루스칼 알고리즘에 비해 비효율적일 수 있습니다.

복잡도

• 우선순위 큐를 사용할 경우, 시간 복잡도는 O(ElogV) 입니다.
• 프림 알고리즘의 공간 복잡도는 O(V)입니다. 우선순위 큐에 모든 노드를 저장할 수 있어야 하기 때문입니다.

예시

구현

import Foundation

struct Edge: Comparable {
    var node: Int
    var weight: Int
    
    static func < (lhs: Edge, rhs: Edge) -> Bool {
        return lhs.weight < rhs.weight
    }
}

struct Heap {
    var elements: [Edge] = []
    
    let sort: (Edge, Edge) -> Bool
    
    init(sort: @escaping (Edge, Edge) -> Bool, elements: [Edge] = []) {
        self.sort = sort
        self.elements = elements
        
        if !elements.isEmpty {
            for i in stride(from: count / 2 - 1, through: 0, by: -1) {
                siftDown(from: i)
            }
        }
    }
    
    var isEmpty: Bool {
        elements.isEmpty
    }
    
    var count: Int {
        elements.count
    }
    
    func peek() -> Edge? {
        elements.first
    }
    
    private func leftChildIndex(ofParentAt index: Int) -> Int {
        (index * 2) + 1
    }
    
    private func rightChildIndex(ofParentAt index: Int) -> Int {
        (index * 2) + 2
    }
    
    private func parentIndex(ofChildAt index: Int) -> Int {
        (index - 1) / 2
    }
    
    private mutating func siftDown(from index: Int) {
        var parent = index
        
        while true {
            let left = leftChildIndex(ofParentAt: parent)
            let right = rightChildIndex(ofParentAt: parent)
            var candidate = parent
            
            if left < count && sort(elements[left], elements[candidate]) {
                candidate = left
            }
            
            if right < count && sort(elements[right], elements[candidate]) {
                candidate = right
            }
            
            if candidate == parent {
                return
            }
            elements.swapAt(parent, candidate)
            parent = candidate
        }
    }
    
    private mutating func siftUp(from index: Int) {
        var child = index
        var parent = parentIndex(ofChildAt: child)
        while child > 0 && sort(elements[child], elements[parent]) {
            elements.swapAt(child, parent)
            child = parent
            parent = parentIndex(ofChildAt: child)
        }
    }
    
    mutating func remove() -> Edge? {
        guard !isEmpty else { return nil }
        
        elements.swapAt(0, count - 1)
        
        defer {
            siftDown(from: 0)
        }
        
        return elements.removeLast()
    }
    
    mutating func insert(_ element: Edge) {
        elements.append(element)
        
        siftUp(from: elements.count - 1)
    }
}

struct PriorityQueue {
    private var heap: Heap
    
    init(sort: @escaping (Edge, Edge) -> Bool, elements: [Edge] = []) {
        heap = Heap(sort: sort, elements: elements)
    }
    
    var isEmpty: Bool {
        heap.isEmpty
    }
    
    var peek: Edge? {
        heap.peek()
    }
    
    @discardableResult
    mutating func enqueue(_ element: Edge) -> Bool {
        heap.insert(element)
        return true
    }
    
    mutating func dequeue() -> Edge? {
        heap.remove()
    }
}

func prim(graph: [[(node: Int, weight: Int)]], startNode: Int) -> Int {
    var totalWeight = 0
    var visited = [Bool](repeating: false, count: graph.count)
    
    let startEdge = Edge(node: startNode, weight: 0)
    
    var pq: PriorityQueue = PriorityQueue(sort: <, elements: [startEdge])
    
    while !pq.isEmpty {
        let edge = pq.dequeue()!
        
        // 해당 노드가 방문되었을때 분기처리
        if visited[edge.node] { continue }
        
        visited[edge.node] = true
        totalWeight += edge.weight
        
        for neighbor in graph[edge.node] {
            // 이웃 노드가 visited 되지 않았다면 enqueue
            // 이 부분은 효율성을 위한 분기 처리
            if !visited[neighbor.node] {
                let edge = Edge(node: neighbor.node, weight: neighbor.weight)
                pq.enqueue(edge)
            }
        }
    }
    
    return totalWeight
}

let nodeCount = 7
var graph = [[(node: Int,  weight: Int)]](repeating: [(node: Int, weight: Int)](), count: nodeCount + 1)

let edges = [
    (1,2,29),
    (1,5,75),
    (2,3,35),
    (2,6,34),
    (3,4,7),
    (4,6,23),
    (4,7,13),
    (5,6,53),
    (6,7,25)
]

// 양방향 인접 리스트로 저장
for edge in edges {
    graph[edge.0].append((node: edge.1, weight: edge.2))
    graph[edge.1].append((node: edge.0, weight: edge.2))
}

prim(graph: graph, startNode: 6)

159 

크루스칼 vs 프림

크루스칼

• 작동 방식

  • 크루스칼 알고리즘은 그래프의 모든 간선을 가중치에 따라 오름차순으로 정렬한 뒤, 가장 가중치가 낮은 간선부터 선택하여 작동합니다.

• 선택 기준

  • 가중치가 가장 낮은 간선부터 선택하되, 사이클이 형성하지 않는 간선만을 선택합니다.

• 사용 자료구조

  • Disjoint Set 자료구조를 사용하며, 사이클 형성 여부를 판단합니다.

• 적용 상황

  • 그래프가 희소일 때(즉, 간선의 수가 노드의 수에 비해 상대적으로 적을 때) 더 효율적 입니다.

프림

• 작동 방식

  • 프림 알고리즘은 그래프의 임의 노드에서 시작하며, 점진적으로 최소 신장 트리를 확장해 나갑니다.

• 선택 기준

  • 이미 선택된 노드들에 인접한 간선들 중에서 가장 가중치가 낮은 간선을 선택합니다.

• 사용 자료구조

  • Priority Queue를 사용하여 다음에 추가할 간선을 효율적으로 선택합니다.

• 적용 상황

  • 그래프가 밀집되어 있을 때(즉, 간선의 수가 노드의 수에 비해 많을 때) 더 효율적입니다.

결론

• 두 알고리즘 모두 그래프의 모든 노드를 포함하는 최소 신장 트리를 찾는데 최적화 되어있습니다.
• 주된 차이점은 알고리즘 접근 방식에 있는데, 프림 알고리즘은 점진적인 확장 방식을 사용하고 크루스칼 알고리즘은 전체 간선을 고려하는 방식을 사용합니다.

예제

도시 분할 계획 - 백준 1647 G4

전력난 - 백준 6497 G4

행성 터널 - 백준 2887 P5

출처(참고문헌)

• 이것이 코딩 테스트이다 - 나동빈
• https://www.kodeco.com/books/data-structures-algorithms-in-swift/v4.0/chapters/44-prim-s-algorithm

제가 학습한 내용을 요약하여 정리한 것입니다. 내용에 오류가 있을 수 있으며, 어떠한 피드백도 감사히 받겠습니다.

감사합니다.