
주제: 특정 노드에서의 최단거리 찾기
다익스트라 알고리즘
- 다익스트라 알고리즘은 그래프 상에서 하나의 시작 정점에서 다른 모든 정점으로 가는 최단 경로를 찾는 알고리즘 입니다.
- 이는 무방향 그래프나 방향 그래프에 모두 적용될 수 있으며, 각 간선에 부여된 가중치는 음수가 아니어야 합니다. 또한 다익스트라 알고리즘은 그리디 알고리즘의 일종으로, 매 단계에서 가장 비용이 적은 노드를 선택하여 경로를 구성합니다.
- '음의 간선'이 없을 때 정장석으로 작동하며, 음의 가선이란 0보다 작은 값을 가지는 간선을 의미하는데 현실 세계의 길은 음의 간선으로 표현되지 않으므로 다익스트라 알고리즘은 실제로 GPS 소프트웨어의 기본 알고리즘으로 채택되곤 합니다.
- 다익스트라 최단 경로 알고리즘은 기본적으로 그리디 알고리즘으로 분류됩니다.
매번 '가장 비용이 적은 노드'를 선택해서 임의의 과정을 반복하기 때문입니다. 하지만 종종 일부 단계가 비용이 더 들더라도 전체 비용이 더 낮은 솔루션을 놓치기도 합니다. 그럼에도 불구하고 매우 빠르고 꽤 좋은 결과를 도출합니다.
동작 방식
- 출발 노드를 설정
- 알고리즘의 시작점이 되는 노드를 설정합니다.
- 최단 거리 테이블을 초기화
- 모든 노드에 대한 최단 거리를 무한으로 설정하고, 시작 노드의 최단 거리는 0으로 설정합니다.
- 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택
- 아직 처리하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택합니다.
- 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신
- 위 과정에서 3과 4번을 반복
효율성
- 다익스트라 알고리즘은 효율적인 우선순위 큐(Priority Queue)를 이용하여 구현할 때 가장 효율적입니다.
- 우선순위 큐를 사용하는 다익스트라 알고리즘의 시간 복잡도는
O(E logV)입니다. 여기서V는 노드의 개수,E는 간선의 개수입니다.
한계
- 음의 가중치가 있는 간선을 포함하는 그래프에서는 다익스트라 알고리즘을 사용할 수 없습니다.
- 모든 간선의 가중치가 동일한 경우, 더 간단한 BFS 알고리즘을 사용하는 것이 더 효율적일 수 있습니다.
활용
- 전염성 관련 생물학적 질병이 가장 빠르게 확산되는 지역을 발견할 수 있습니다.
- 네트워크에서 가장 대역폭이 높은 경로에 전화를 라우팅할 수 있습니다.
- 여행객을 위한 가장 짧고 빠른 경로를 찾을 수 있습니다.

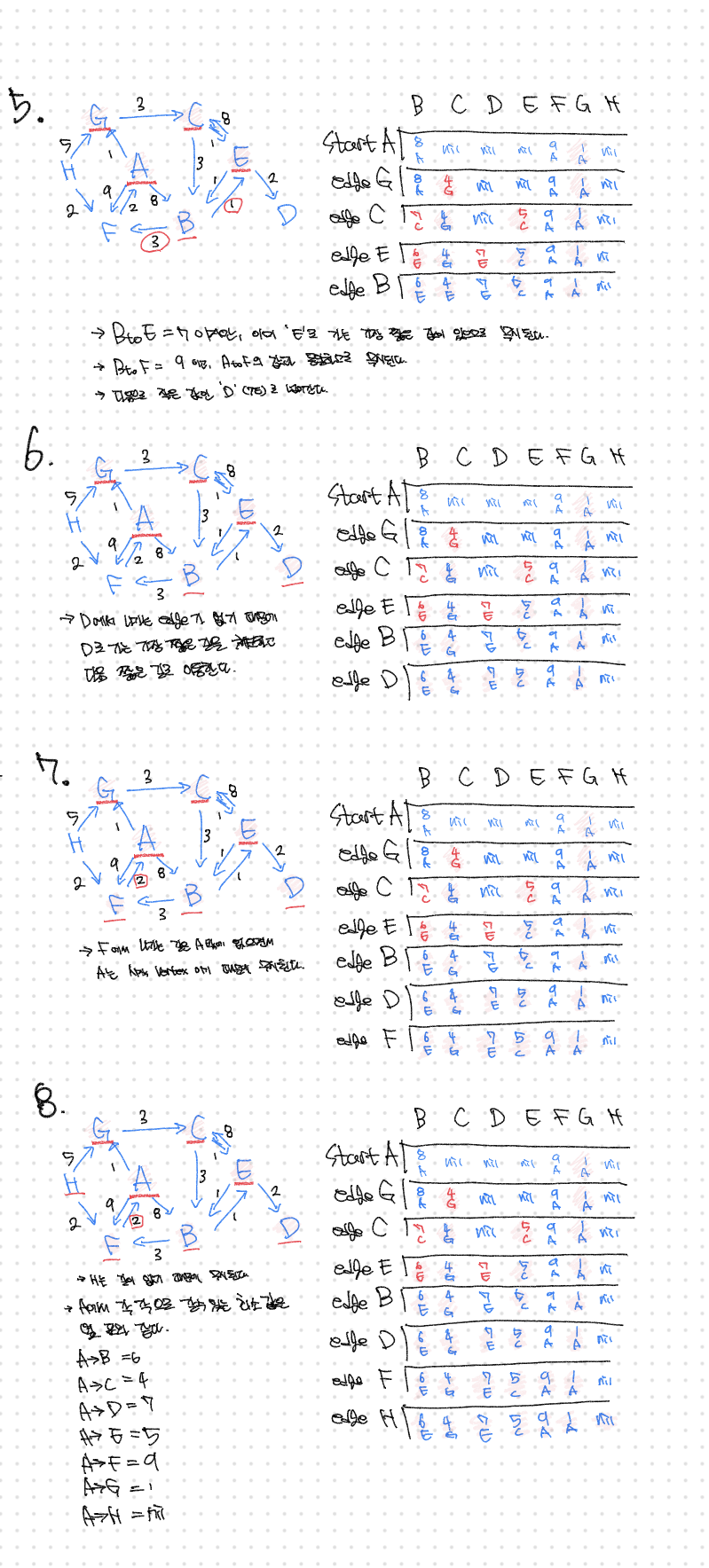
구현
그래프를 활용한 방법
- 다익스트라 알고리즘을 구현하기 앞서, 인접 리스트 그래프와 우선순위 큐 구현이 필요합니다.
우선순위 큐
- 우선순위 큐는 아직 방문하지 않은 정점(Vertex)들의 저장을 위해서 필요합니다.
struct PrioirtyQueueArray<T: Equatable> {
private var elements:[T] = []
let sort: (T,T) -> Bool
init(sort: @escaping (T,T) -> Bool, elements: [T] = []) {
self.sort = sort
self.elements = elements
self.elements.sort(by: sort)
}
public var isEmpty: Bool {
elements.isEmpty
}
public var peek: T? {
elements.first
}
public mutating func enqueue(_ element: T) -> Bool {
for (index, otherElement) in elements.enumerated() {
if sort(element, otherElement) {
elements.insert(element, at: index)
return true
}
}
elements.append(element)
return true
}
public mutating func dequeue() -> T? {
isEmpty ? nil : elements.removeFirst()
}
}그래프
public enum EdgeType {
case directed
case undirected
}
public struct Vertex<T> {
public let index: Int
public let data: T
}
extension Vertex: Hashable where T: Hashable {}
extension Vertex: Equatable where T: Equatable {}
public struct Edge<T> {
public let source: Vertex<T>
public let destination: Vertex<T>
public let weight: Double?
}
public class AdjacencyList<T: Hashable> {
private var adjacencies: [Vertex<T>: [Edge<T>]] = [:]
public init() { }
public func createVertex(data: T) -> Vertex<T> {
let vertex = Vertex(index: adjacencies.count, data: data)
adjacencies[vertex] = []
return vertex
}
public func addDirectedEdge(from source: Vertex<T>, to destination: Vertex<T>, weight: Double?) {
let edge = Edge(source: source, destination: destination, weight: weight)
adjacencies[source]?.append(edge)
}
public func addUndirectedEdge(between source: Vertex<T>, and destination: Vertex<T>, weight: Double?) {
addDirectedEdge(from: source, to: destination, weight: weight)
addDirectedEdge(from: destination, to: source, weight: weight)
}
public func add(_ edge: EdgeType, from source: Vertex<T>, to destination: Vertex<T>, weight: Double?) {
switch edge {
case .directed:
addDirectedEdge(from: source, to: destination, weight: weight)
case .undirected:
addUndirectedEdge(between: source, and: destination, weight: weight)
}
}
public func edges(from source: Vertex<T>) -> [Edge<T>] {
adjacencies[source] ?? []
}
public func weight(from source: Vertex<T>, to destination: Vertex<T>) -> Double? {
edges(from: source)
.first { $0.destination == destination }?
.weight
}
}다익스트라 알고리즘 구현 (인접 리스트 활용)
public enum Visit<T: Hashable> {
case start
case edge(Edge<T>)
}start는 시작 정점을 의미합니다.edge(Edge<T>)는 시작 정점으로 되돌아가는 경로로 이어지는 관련 간선을 가지고 있습니다.
public class Dijkstra<T: Hashable> {
public typealias Graph = AdjacencyList<T>
let graph: Graph
public init(graph: Graph) {
self.graph = graph
} // 현재 vertex에서 시작 vertex까지의 총 Weight를 추적할 수 있는 메커니즘
private func route(to destination: Vertex<T>, with paths: [Vertex<T>: Visit<T>]) -> [Edge<T>] {
var vertex = destination // 1
var path: [Edge<T>] = [] // 2
while let visit = paths[vertex], case .edge(let edge) = visit { // 3
path = [edge] + path // 4
vertex = edge.source // 5
}
return path // 6
}- 이 메서드는
destination정점과 기존 경로를 담은dictionary을 받아들이고,destination정점으로 이어지는 경로를 생성합니다.
destination정점에서 시작합니다.- 경로를 저장할 간선들의 배열을 생성합니다.
- 시작 정점에 도달할 때까지 다음 간선을 계속해서 추출합니다.
- 현재 간선을 경로에 추가합니다.
- 현재 정점을 해당 간선의 출발 정점으로 설정합니다. 이 할당은 시작 정점에 가까워지도록 이동합니다.
- while 루프가 시작 정점에 도달하면 경로가 완료되고 반환됩니다.
private func distance(to destination: Vertex<T>, with paths: [Vertex<T>: Visit<T>]) -> Double {
let path = route(to: destination, with: paths) // 1
let distances = path.compactMap { $0.weight } // 2
return distances.reduce(0.0, +) // 3
}- 이 메서드는
destination정점과 기존 경로들을 담은dictionary를 받아들여 총 가중치를 반환합니다.
desination으로 가는 경로를 구성합니다.compactMap을 사용하여 경로에서 모든nil가중치 값을 제거합니다.reduce를 사용하여 모든 간선의 가중치를 합산합니다.
public func shortestPath(from start: Vertex<T>) -> [Vertex<T>: Visit<T>] {
var paths: [Vertex<T>: Visit<T>] = [start: .start] // 1
// 2
var priorityQueue = PrioirtyQueueArray<Vertex<T>>(sort: {
self.distance(to: $0, with: paths) < self.distance(to: $1, with: paths)
})
priorityQueue.enqueue(start) // 3- 이 메서드는 시작 정점을 입력받아 모든 경로를 담은
dictionary을 return 합니다.
path를 정의하고 시작 정점으로 초기화합니다.- 방문해야 할 정점들을 저장하기 위한 최소 우선순위 큐를 생성합니다. 정렬은
distance메서드를 사용하여 시작 정점으로부터의 거리에 따라 정점들을 정렬합니다. - 방문할 첫 번째 정점으로 시작 정점을 큐에 추가합니다.
while let vertex = priorityQueue.dequeue() { // 1
for edge in graph.edges(from: vertex) { // 2
guard let weight = edge.weight else { // 3
continue
}
if paths[edge.destination] == nil || distance(to: vertex, with: paths) + weight < distance(to: edge.destination, with: paths) { // 4
paths[edge.destination] = .edge(edge)
priorityQueue.enqueue(edge.destination)
}
}
}
return paths
}- 모든 정점이 방문될 때까지 최단 경로를 찾습니다.
- 현재 정점에 대한 모든 이웃하는 간선들을 확인합니다.
- 간선에 가중치가 있는지 확인합니다. 없다면 다음 간선으로 넘어갑니다.
destination정점이 이전에 방문된 적이 없거나, 더 저렴한 경로를 발견했다면, 경로를 업데이트하고 이웃하는 정점을 우선순위 큐에 추가합니다.
- 모든 정점이 방문되고 우선순위 큐가 비어있다면, 시작 정점으로의 최단 경로를 담은 사전을 반환합니다.
public func shortestPath(to destination: Vertex<T>, paths: [Vertex<T>: Visit<T>]) -> [Edge<T>] {
return route(to: destination, with: paths)
}
- 이 메서드는
destination정점과 최단 경로dictionary을 인자로 받아destination정점으로의 경로를 반환합니다.
public func getAllShortestPath(from source: Vertex<T>) -> [Vertex<T>: [Edge<T>]] {
var pathsDict = [Vertex<T>: [Edge<T>]]()
let pathsFromSource = shortestPath(from: source)
for vertex in graph.vertices {
let path = shortestPath(to: vertex, paths: pathsFromSource)
pathsDict[vertex] = path
}
return pathsDict
}
}let dijkstraList = DijkstraList(graph: graph1)
let pathsFromA = dijkstraList.shortestPath(from: tokyo)
let path = dijkstraList.shortestPath(to: seattle, paths: pathsFromA)
for edge in path {
print("\(edge.source) --|\(edge.weight ?? 0.0)|--> \(edge.destination)")
}
let allPath = dijkstraList.getAllShortestPath(from: tokyo)
for path in allPath {
for edges in path.value {
print("\(edges.source) --|\(edges.weight ?? 0.0)|--> \(edges.destination)")
}
print()
}
1: Tokyo --|300.0|--> 5: Washington DC
5: Washington DC --|277.0|--> 7: Seattle
1: Tokyo --|300.0|--> 5: Washington DC
1: Tokyo --|450.0|--> 3: Detroit
3: Detroit --|50.0|--> 6: Austin Texas
6: Austin Texas --|297.0|--> 4: San Francisco
1: Tokyo --|450.0|--> 3: Detroit
1: Tokyo --|450.0|--> 3: Detroit
3: Detroit --|50.0|--> 6: Austin Texas
Input값이 주어졌을때 방법
간단 구현
- 간단한 다익스트라 알고리즘은 의 시간 복잡도를 가지며, 다익스트라에 의해서 처음 고안되었던 알고리즘이다. 여기서 V는 노드의 개수를 의미합니다.
- 이 알고리즘은 직관적이고 쉽게 이해할 수 있으며, 처음에 각 노드에 대한 최단 거리를 담는 1차원 리스트를 선언합니다.
- 이후에 단계마다 '방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택' 하기 위해 매 단계마다 1차원 리스트의 모든 원소를 확인 순차 탐색합니다.
- (노드의 개수 + 1)의 크기로 할당하여, 노드의 번호를 인덱스로 하여 바로 리스트에 접근할 수 있도록 조정 합니다.
import Foundation
// 최댓값
let INF = Int.max
// 노드의 개수
let nodeCount: Int = 6
// 간선의 개수
let link: Int = 11
// 시작 노드 번호
let start: Int = 1
// 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열
var graph = [[[Int]]](repeating: [[Int]](), count: nodeCount + 1)
// 방문한 적이 있는지 체크하는 목적의 배열
var visited = [Bool](repeating: false, count: nodeCount + 1)
// 최단 거리 테이블을 모두 무한으로 초기화
var distance = [Int](repeating: INF, count: nodeCount + 1)
// 모든 간선 정보 입력받기
// a번 노드에서 b번 노드로 가는 비용이 c라는 의미
for _ in 1...link {
let array = readLine()!.components(separatedBy: " ").map { Int($0)!}
let a = array[0]
let b = array[1]
let c = array[2]
graph[a].append([b,c])
}
// 방문하지 않은 노드 중에서, 가장 최단 거리가 짧은 노드의 번호를 반환
func get_smallest_node() -> Int {
var min_value = INF
// 가장 최단 거리가 짧은 노드(인덱스)
var index = 0
for i in 1...nodeCount {
if distance[i] < min_value && !visited[i] {
min_value = distance[i]
index = i
}
}
return index
}
func dijkstra(_ start: Int) {
distance[start] = 0
visited[start] = true
for i in graph[start] {
distance[i[0]] = i[1]
}
// 시작 노드를 제외한 전체 n-1개의 노드에 대해 반복
for _ in 0..<nodeCount {
// 현재 최단 거리가 가장 짧은 노드를 꺼내서, 방문 처리
let now = get_smallest_node()
visited[now] = true
// 현재 노드와 연결된 다른 노드를 확인
for j in graph[now] {
let cost = distance[now] + j[1]
if cost < distance[j[0]] {
distance[j[0]] = cost
}
}
}
}
dijkstra(start)
for i in 1...nodeCount {
if distance[i] == INF {
print("INFINITY")
} else {
print("\(i): ", distance[i])
}
}- 코딩 테스트의 최단 경로 문제에서 전체 노드의 개수가 5,000개 이하라면 일반적으로 이 코드로 문제를 풀 수 있을것 입니다. 하지만 노드의 개수가 10,000개를 넘어가는 문제라면 이 코드로는 문제를 해결하기 어렵습니다.
개선된 구현
- 개선된 다익스트라 알고리즘은 시간복잡도 O(ElogV)를 보장합니다. 여기서 V는 노드의 개수이고 E는 간선의 개수입니다.
- 간단한 다익스트라 알고리즘은 '최단 거리가 가장 짧은 노드'를 찾기 위해, 매번 최단 거리 테이블을 선형적으로 (모든 원소를 앞에서부터 하나씩) 탐색해야 했으며, 이 과정에서만 O(V)의 시간이 걸렸습니다. 하지만 최단 거리가 가장 짧은 노드를 단순히 선형적으로 찾는 것이 아니라 힙 자료구조를 활용하면 쉽게 처리할 수 있습니다.
- 즉, 현재 가장 가까운 노드를 저장하기 위한 목적으로만 우선순위 큐를 추가로 이용한다고 보면 됩니다.
- 우선순위 큐에서 노드를 꺼낸 뒤에 해당 노드를 이미 처리한 적이 있다면 무시하면 되고, 아직 처리하지 않은 노드에 대해서만 처리하면 됩니다.
- 앞의 코드와 비교했을 때 get_smallest_node()라는 함수를 작성할 필요가 없다는 특징이 있습니다.
struct Heap {
var elements = [(Int,Int)]()
let sort: (Int,Int) -> Bool
init(elements: [(Int,Int)] = [(Int,Int)](), sort: @escaping (Int, Int) -> Bool) {
self.elements = elements
self.sort = sort
if !elements.isEmpty {
for i in stride(from: count / 2 - 1, through: 0, by: -1) {
siftDown(from: i)
}
}
}
var isEmpty: Bool {
elements.isEmpty
}
var count: Int {
elements.count
}
func peek() -> (Int,Int)? {
elements.first
}
private func leftChildIndex(ofParentAt index: Int) -> Int {
(2 * index) + 1
}
private func rightChildIndex(ofParentAt index: Int) -> Int {
(2 * index) + 2
}
private func parentIndex(ofChildAt index: Int) -> Int {
(index - 1) / 2
}
private mutating func siftDown(from index: Int) {
var parent = index
while true {
let left = leftChildIndex(ofParentAt: parent)
let right = rightChildIndex(ofParentAt: parent)
var candidate = parent
if left < count && sort(elements[left].1, elements[candidate].1) {
candidate = left
}
if right < count && sort(elements[right].1, elements[candidate].1) {
candidate = right
}
if candidate == parent {
return
}
elements.swapAt(parent, candidate)
parent = candidate
}
}
private mutating func siftUp(from index: Int) {
var child = index
var parent = parentIndex(orParentAt: child)
while child > 0 && sort(elements[child].1, elements[parent].1) {
elements.swapAt(child, parent)
child = parent
parent = parentIndex(orParentAt: child)
}
}
mutating func remove() -> (Int,Int)? {
guard !isEmpty else {
return nil
}
elements.swapAt(0, count - 1)
defer {
siftDown(from: 0)
}
return elements.removeLast()
}
mutating func insert(_ element: (Int,Int)) {
elements.append(element)
siftUp(from: elements.count - 1)
}
}
struct PriorityQueue {
private var heap: Heap
init(sort: @escaping (Int,Int) -> Bool, elements:[(Int,Int)] = []) {
heap = Heap(elements: elements,sort: sort)
}
var isEmpty: Bool {
heap.isEmpty
}
var peek: (Int,Int)? {
heap.peek()
}
@discardableResult mutating func enqueue(_ element: (Int,Int)) -> Bool {
heap.insert(element)
return true
}
mutating func dequeue() -> (Int,Int)? {
heap.remove()
}
}
let INF = Int.max
let line = readLine()!.components(separatedBy: " ").map { Int($0)!}
// 노드
var n = line[0]
// 간선
var m = line[1]
// 시작 노드 번호를 입력받기
let start = Int(readLine()!)!
// 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트 만들기
var graph = [[(Int,Int)]](repeating:[(Int,Int)](), count: n + 1)
// 최단 거리 테이블을 모두 무한으로 초기화
var distance = [Int](repeating: INF, count: n + 1)
// 모든 간선 정보 입력받기
for _ in 0..<m {
let line2 = readLine()!.components(separatedBy: " ").map { Int($0)!}
let a = line2[0]
let b = line2[1]
let c = line2[2]
// a번 노드에서 b번 노드로 가는 비용이 c
graph[a].append((b,c))
}
func dijkstra(_ start: Int) {
var queue = PriorityQueue(sort: <, elements: [(start,0)])
distance[start] = 0
while !queue.isEmpty {
// 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
let queueValue = queue.dequeue()!
let dist = queueValue.1
let nowNode = queueValue.0
// 현재 노드가 이미 처리된 적이 있다면 무시
if distance[nowNode] < dist {
continue
}
// 현재 노드와 연결된 다른 인접한 노드들을 확인
for i in graph[nowNode] {
let cost = dist + i.1
if cost < distance[i.0] {
distance[i.0] = cost
queue.enqueue((i.0,cost))
}
}
}
}예제 - 전보 (이것이 코딩 테스트이다. 나동빈)
문제
- 어떤 나라에는 N개의 도시가 있다.
- 그리고 각 도시는 보내고자 하는 메시지가 있는 경우, 다른 도시로 전보를 보내서 다른 도시로 해당 메시지를 전송할 수 있다.
- 하지만 X라는 도시에서 Y라는 도시로 전보를 보내고자 한다면, 도시 X에서 Y로 향하는 통로가 설치되어 있어야 한다.
- 예를 들어 X에서 Y로 향하는 통로는 있지만, Y에서 X로 향하는 통로가 없다면 Y는 X로 메시지를 보낼 수 없다.
- 또한 통로를 거쳐 메시지를 보낼 때는 일정 시간이 소요된다.
- 어느 날 C라는 도시에서 위급 상황이 발생했다. 그래서 최대한 많은 도시로 메시지를 보내고자 한다.
- 메시지는 도시 C에서 출발하여 각 도시 사이에 설치된 통로를 거쳐, 최대한 많이 퍼져나갈 것이다.
- 각 도시의 번호와 통로가 설치되어 있는 정보가 주어졌을 때,
- 도시 C에서 보낸 메시지를 받게 되는 도시의 개수는 총 몇 개이며
- 도시들이 모두 메시지를 받는 데까지 걸리는 시간은 얼마인지 계산하는 프로그램을 작성하시오.
입력 조건
- 첫째 줄에 도시의 개수 N, 통로의 개수 M, 메시지를 보내고자 하는 도시 C가 주어진다.
- (1 <= N <= 30,000, 1 <= M <= 200,000, 1 <= C <= N)
- 둘째 줄부터 M + 1번째 줄에 걸쳐서 통로에 대한 정보 X, Y, Z가 주어진다.
- 이는 특정 도시 X에서 다른 특정 도시 Y로 이어지는 통로가 있으며, 메시지가 전달되는 시간이 Z라는 의미다.
- (1 <= X, Y <= N, 1 <= Z <= 1,000)
출력 조건
- 첫째 줄에 도시 C에서 보낸 메시지를 받는 도시의 총 개수와 총 걸리는 시간을 공백으로 구분하여 출력한다.
입력 예시
3 2 1
1 2 4
1 3 2출력 예시
2 4풀이
- 문제를 잘 확인해보면, 최단거리 문제입니다. 다익스트라 알고리즘을 활용해서 도시 C에서 보낸 메시지를 받게 되는 도시의 개수를 쉽게 구할 수 있으며 또한 모두 메시지를 받는 데까지 걸리는 시간은 도시 C와 연결된 도시 중 가장 가중치가 큰 값을 고르면 된다.
import Foundation
struct Heap {
var elements = [(Int, Int)]()
let sort: (Int, Int) -> Bool
init(elements: [(Int, Int)] = [(Int, Int)](), sort: @escaping (Int, Int) -> Bool) {
self.elements = elements
self.sort = sort
if !elements.isEmpty {
for i in stride(from: count / 2 - 1, through: 0, by: -1) {
siftDown(from: i)
}
}
}
var isEmpty: Bool {
elements.isEmpty
}
var count: Int {
elements.count
}
func peek() -> (Int, Int)? {
elements.first
}
private func leftChildIndex(ofParentAt index: Int) -> Int {
(2 * index) + 1
}
private func rightChildIndex(ofParentAt index: Int) -> Int {
(2 * index) + 2
}
private func parentIndex(ofchildAt index: Int) -> Int {
(index - 1) / 2
}
private mutating func siftDown(from index: Int) {
var parent = index
while true {
let left = leftChildIndex(ofParentAt: parent)
let right = rightChildIndex(ofParentAt: parent)
var candidate = parent
if left < count && sort(elements[left].1, elements[candidate].1) {
candidate = left
}
if right < count && sort(elements[right].1, elements[candidate].1) {
candidate = right
}
if candidate == parent {
return
}
elements.swapAt(parent, candidate)
parent = candidate
}
}
private mutating func siftUp(from index: Int) {
var child = index
var parent = parentIndex(ofchildAt: child)
while child > 0 && sort(elements[child].1, elements[parent].1) {
elements.swapAt(child, parent)
child = parent
parent = parentIndex(ofchildAt: child)
}
}
mutating func remove() -> (Int, Int)? {
guard !isEmpty else {
return nil
}
elements.swapAt(0, count - 1)
defer {
siftDown(from: 0)
}
return elements.removeLast()
}
mutating func insert(_ element: (Int, Int)) {
elements.append(element)
siftUp(from: elements.count - 1)
}
}
struct PriorityQueue {
private var heap: Heap
init(sort: @escaping (Int,Int) -> Bool, elements:[(Int,Int)] = []) {
heap = Heap(elements: elements,sort: sort)
}
var isEmpty: Bool {
heap.isEmpty
}
var peek: (Int,Int)? {
heap.peek()
}
@discardableResult mutating func enqueue(_ element: (Int,Int)) -> Bool {
heap.insert(element)
return true
}
mutating func dequeue() -> (Int,Int)? {
heap.remove()
}
}
let INF = Int.max
let testCase = readLine()!.components(separatedBy: " ").map { Int($0)! }
// 도시의 총 개수
let n = testCase[0]
// 통로의 총 개수
let m = testCase[1]
// 메시지 보내는 도시
let start = testCase[2]
// destination / weight
var graph = [[(Int, Int)]](repeating: [(Int, Int)](), count: n + 1)
var distance = [Int](repeating: INF, count: n + 1)
var visited = [Bool](repeating: false, count: n + 1)
for _ in 0..<m {
let test = readLine()!.components(separatedBy: " ").map { Int($0)! }
// to destination weight
graph[test[0]].append((test[1], test[2]))
}
func dijkstra(_ start: Int) {
// queue에 값을 넣고 시작합니다. 이때 시작값의 weight 값 추가, 방문처리를 진행합니다.
var queue = PriorityQueue(sort: <, elements: [(start, 0)])
distance[start] = 0
visited[start] = true
// queue가 비워질때까지 진행합니다.
while !queue.isEmpty {
// queue의 최신값을 뽑아내며, 그 값을 활용합니다.
let value = queue.dequeue()!
let vertex = value.0
let weight = value.1
// distance에 있는 값이 weight보다 작다면 즉, 기존값이 더 작다면 넘어갑니다.
if distance[vertex] < weight {
continue
}
// 현재 Vertex의 Destination들을 확인합니다.
for i in graph[vertex] {
// 현재 vertex에서 destination으로 가는 값을 현재 vertex의 최단거리와 더해줍니다.
let newWeight = weight + i.1
// 더해준 값이 작다면, 해당값으로 값을 변경해주고 enqueue 해줍니다.
if newWeight < distance[i.0] {
distance[i.0] = newWeight
visited[i.0] = true
queue.enqueue((i.0, newWeight))
}
}
}
}
dijkstra(start)
var result1 = 0
var result2 = Int.min
for i in 1...n {
if i > 1 && visited[i] == true {
result1 += 1
}
result2 = max(distance[i], result2)
}
print("\(result1) \(result2)")결론
- 최단 경로를 찾아야 하는 문제가 출제되었을 때, 노드의 개수가 적은 경우에는 플로이드 워셜 알고리즘을 이용할 수 있다.
- 반면에 노드와 간선의 개수가 모두 많으면 우선순위 큐를 이용하는 다익스트라 알고리즘을 이용하면 유리하다.
출처(참고문헌)
- https://www.kodeco.com/books/data-structures-algorithms-in-swift/v4.0/chapters/42-dijkstra-s-algorithm
- 이것이 코딩 테스트이다. 나동빈
제가 학습한 내용을 요약하여 정리한 것입니다. 내용에 오류가 있을 수 있으며, 어떠한 피드백도 감사히 받겠습니다.
감사합니다.
