[Data Structure / Algorithms] Topology Sort (위상정렬)

전성훈·2023년 11월 17일
Algorithmsdatastructureswift
0

Data Structure-Algorithm

목록 보기
33/35
post-thumbnail

주제: 방향 그래프에서 모든 노드의 방향성 나열하기

위상정렬 이란

  • 위상 정렬은 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘 입니다.
  • 즉, 위상 정렬은 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열한 것입니다.
  • 다시 말해 그래프상에서 선후관계가 있다면, 위상 정렬을 수행하여 모든 선후 관계를 지키는 전체 순서를 계산할 수 있습니다.

특징

  • 위상 정렬은DAG(Directed Acyclic Graph, 유향 비순환 그래프(사이클이 없는 그래프))에서만 수행될 수 있습니다.
  • 하나의 그래프에서 여러 위상 정렬 결과가 나올 수 있습니다.
  • 복잡한 종속성을 가진 작업들의 실행 순서를 결정할 수 있습니다.
  • 또한, 순환 참조 즉, 순환 의존성(Circular Dependency)의 존재 여부를 파악할 수 있습니다.
  • 모든 노드와 간선을 고려해야 하므로, 그래프가 크면 처리 시간이 길어질 수 있습니다.

Kahn's Algorithms

구현 방법

  1. 먼저 그래프의 모든 노드에 대해 진입 차수(해당 노드로 들어오는 간선의 수)를 계산합니다.
  2. 진입 차수가 0인 노드, 즉 다른 노드로부터 들어오는 간선이 없는 노드를 찾아 큐에 삽입합니다.
  3. BFS를 수행합니다.
    3-1. 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거합니다.
    3-2. 새롭게 진입차수가 0이 된 노드를 큐에 넣습니다.
  4. 위의 과정을 모든 노드가 큐에서 나올 때까지 반복합니다. 이 때, 큐에서 나온 순서가 그래프의 위상 정렬 순서가 됩니다.
  • 이 방법의 장점은 순환 의존성이 있는 경우(그래프의 사이클이 있는 경우) 쉽게 탐지할 수 있다는 것 입니다.
  • 만약 그래프의 모든 노드를 방문하기 전에 큐가 비어버린다면, 그래프에 사이클이 존재한다는 의미이며, 이 경우 정상적인 위상 정렬이 불가능합니다.
  • 해당 알고리즘을 활용해서 그래프의 사이클을 판별할 수 있습니다. 모든 노드가 큐에서 처리되면 그래프는 사이클이 없는 것입니다. 즉, 큐의 작업이 모든 노드를 방문하기 전에 종료된다면 사이클이 있다고 판단 할 수 있습니다.

복잡도

  • 시간 복잡도는 O(V+E)O(V + E) 입니다. 여기서 VV는 노드의 수, EE는 간선의 수 입니다.
  • 공간 복잡도는 O(V)O(V) 입니다. 각 노드의 진입 차수와 큐에 노드를 저장하는 데 필요한 공간입니다.

예시

구현

import Foundation

// Ring Buffer를 활용한 Queue
struct RingBuffer {
    private var array: [Int?]
    private var readIndex = 0
    private var writeIndex = 0
    
    init(count: Int) {
        array = Array(repeating: nil, count: count)
    }
    
    var first: Int? {
        array[readIndex]
    }
    
    private var availableSpaceForReading: Int {
        writeIndex - readIndex
    }
    
    private var availableSpaceForWriting: Int {
        array.count - availableSpaceForReading
    }
    
    var isEmpty: Bool {
        availableSpaceForReading == 0
    }
    
    var isFull: Bool {
        availableSpaceForWriting == 0
    }
    
    @discardableResult
    mutating func write(_ element: Int) -> Bool {
        if !isFull {
            array[writeIndex % array.count] = element
            writeIndex += 1
            
            return true
        } else {
            return false
        }
    }
    
    mutating func read() -> Int? {
        if !isEmpty {
            let element = array[readIndex % array.count]
            readIndex += 1
            
            return element
        } else {
            return nil
        }
    }
}

// RingBuffer를 활용한 Queue 생성 
struct Queue {
    private var ringBuffer: RingBuffer
    
    init(count: Int) {
        ringBuffer = RingBuffer(count: count)
    }
    
    var isEmpty: Bool {
        ringBuffer.isEmpty
    }
    
    var peek: Int? {
        ringBuffer.first
    }
    
    @discardableResult
    mutating func enqueue(_ element: Int) -> Bool {
        ringBuffer.write(element)
    }
    
    mutating func dequeue() -> Int? {
        ringBuffer.read()
    }
}

// Kahn's Algorithms
func topologicalSortKahn(graph: [[Int]], vertices: Int) -> [Int]? {
    // 진입 차수를 위한 배열
    // 최초 '0'으로 초기화
    var inDegree = [Int](repeating: 0, count: vertices)
    // 링 버퍼 큐는 최대 N개 즉 노드의 개수만큼의 크기를 할당해야한다.
    // 최악의 경우 모든 차수가 0일수도 있기 때문이다.
    var queue = Queue(count: vertices - 1)
    // 정렬된 노드를 저장하는 배열
    var order: [Int] = []
    
    // 진입 차수 계산
    // 인접 리스트 그래프 활용
    for node in graph {
        for edge in node {
            inDegree[edge] += 1
        }
    }
    
    // 진입 차수가 0인 노드 큐에 추가
    for i in 1..<inDegree.count {
        if inDegree[i] == 0 {
            queue.enqueue(i)
        }
    }
    
    // BFS 수행
    while !queue.isEmpty {
        let node = queue.dequeue()!
        order.append(node)
        
        for edge in graph[node] {
            inDegree[edge] -= 1
            if inDegree[edge] == 0 {
                queue.enqueue(edge)
            }
        }
    }
    
    // 모든 노드가 처리되었는지 확인
    // 즉 큐가 조기 종료되면 order count가 vertices와 다름
    if order.count == vertices - 1 {
        return order
    } else {
        return nil
    }
}

// 예시 그래프 사용
let n = 7
let graph = [[], [2,5],[3,6],[4],[7],[6],[4],[]]
let graph2 = [[], [2,5],[3],[4,6],[7],[6],[4,2],[]]


if let sorted = topologicalSortKahn(graph: graph, vertices: n + 1) {
    print("위상 정렬 결과: \(sorted)")
} else {
    print("사이클이 존재합니다.")
}


if let sorted = topologicalSortKahn(graph: graph2, vertices: n + 1) {
    print("위상 정렬 결과: \(sorted)")
} else {
    print("사이클이 존재합니다.")
}

위상 정렬 결과: [1, 2, 5, 3, 6, 4, 7]
사이클이 존재합니다.

Topological Sorting Using DFS

구현 방법

  1. 방문상태를 저장할 배열과, 위상 정렬 결과를 저장할 스택을 생성합니다.
  2. DFS 함수를 활용해서 임의의 노드를 방문하고, 그 노드의 모든 인접 노드에 대해 재귀적으로 DFS를 호출합니다.
  3. 한 노드의 모든 인접 노드를 방문한 후, 해당 노드를 스택에 push합니다. 이는 해당 노드에서 출발하는 모든 간선이 처리되었음을 의미합니다.
  4. 모든 노드에 대해 DFS를 완료한 후, 스택에 저장된 순서를 뒤집으면 위상 정렬의 결과값이 됩니다.
  • DFS를 사용하면서 위상 정렬과 함께 사이클의 존재 여부도 확인할 수 있습니다.
  • 이는 간단하게, 각 노드의 상태를 방문 x, 방문 중, 방문 완료로 나누며, 방문 중 인 노드를 다시 방문하게 되면, 그래프의 사이클이 존재한다고 판단합니다.
  • 사이클이 없는 경우 위상 정렬 결과를 생성합니다.

복잡도

  • 시간 복잡도는 O(V+E)O(V + E) 입니다. 여기서 VV는 노드의 수, EE는 간선의 수 입니다.
  • 공간 복잡도는 O(V)O(V) 입니다.

예시

구현

enum VisiteState {
    case unvisited, visiting, visited
}

var visited: [VisiteState] = []
var stack: [Int] = []
var hasCycle = false

func dfs(graph: [[Int]], node: Int) {
    // 방문 중일때 방문했을 경우 Cycle 발생
    if visited[node] == .visiting {
        hasCycle = true
        return
    }
    
    // 이미 방문한 node는 무시
    if visited[node] == .visited {
        return
    }
    
    visited[node] = .visiting
    
    for neighbor in graph[node] {
        dfs(graph: graph, node: neighbor)
        if hasCycle { return }
    }
    
    visited[node] = .visited
    // 방문이 다 종료되면 Stack에 Node 추가
    stack.append(node)
}

func topologicalSort(graph: [[Int]], vertices: Int) -> [Int]? {
    visited = [VisiteState](repeating: .unvisited, count: vertices)
    stack = []
    hasCycle = false
    
    // 모든 노드에 대해서 dfs 실행
    for i in 1..<vertices {
        if visited[i] == .unvisited {
            dfs(graph: graph, node: i)
            if hasCycle { return nil }
        }
    }
    
    return stack.reversed()
}

// 예시 그래프 사용
let n = 7
let graph = [[], [2,5],[3,6],[4],[7],[6],[4],[]]
let graph2 = [[], [2,5],[3],[4,6],[7],[6],[4,2],[]]

if let sorted = topologicalSort(graph: graph, vertices: n + 1) {
    print(sorted.map { String($0)}.joined(separator: " "))} else {
    print("사이클이 존재합니다.")
}

if let sorted = topologicalSort(graph: graph2, vertices: n + 1) {
    print(sorted.map { String($0)}.joined(separator: " "))
} else {
    print("사이클이 존재합니다.")
}

1 5 2 6 3 4 7
사이클이 존재합니다.

결론

  • Kahn's Algorithm 은 진입 차수와 큐를 활용해서 위상 정렬를 수행하며, DFS는 재귀 함수를 활용해서 위상 정렬을 수행합니다.

예제

줄 세우기 - 백준 2252 G3

문제

  • N명의 학생들을 키 순서대로 줄을 세우려고 한다. 각 학생의 키를 직접 재서 정렬하면 간단하겠지만, 마땅한 방법이 없어서 두 학생의 키를 비교하는 방법을 사용하기로 하였다. 그나마도 모든 학생들을 다 비교해 본 것이 아니고, 일부 학생들의 키만을 비교해 보았다.
  • 일부 학생들의 키를 비교한 결과가 주어졌을 때, 줄을 세우는 프로그램을 작성하시오.

입력

  • 첫째 줄에 N(1 ≤ N ≤ 32,000), M(1 ≤ M ≤ 100,000)이 주어진다. M은 키를 비교한 회수이다. 다음 M개의 줄에는 키를 비교한 두 학생의 번호 A, B가 주어진다. 이는 학생 A가 학생 B의 앞에 서야 한다는 의미이다.
  • 학생들의 번호는 1번부터 N번이다.

출력

  • 첫째 줄에 학생들을 앞에서부터 줄을 세운 결과를 출력한다. 답이 여러 가지인 경우에는 아무거나 출력한다.

예제 입력 1 

3 2
1 3
2 3

예제 출력 1 

1 2 3

예제 입력 2 

4 2
4 2
3 1

예제 출력 2 

4 2 3 1

풀이

  • 줄 세우기 문제는 간단하다. 주어진 값에 대하여 graph을 만든 후 위상정렬를 수행해, 해당 결과를 출력하면 된다.
  • 문제를 보면 주어진 값이 키를 비교한 두 학생의 번호가 A, B 주어지는데, 이는 학생 A가 B의 앞에 서야 한다는 의미 즉, 방향 간선으로 연결되어 있다는 뜻이다. 그러므로 그래프로 만들어서 위상정렬을 수행하면 된다. 
// MARK: 1. Kahn's Algorithm을 사용하여 문제 해결
import Foundation

// Ring Buffer를 활용한 Queue
struct RingBuffer {
    private var array: [Int?]
    private var readIndex = 0
    private var writeIndex = 0
    
    init(count: Int) {
        array = Array(repeating: nil, count: count)
    }
    
    var first: Int? {
        array[readIndex]
    }
    
    private var availableSpaceForReading: Int {
        writeIndex - readIndex
    }
    
    private var availableSpaceForWriting: Int {
        array.count - availableSpaceForReading
    }
    
    var isEmpty: Bool {
        availableSpaceForReading == 0
    }
    
    var isFull: Bool {
        availableSpaceForWriting == 0
    }
    
    @discardableResult
    mutating func write(_ element: Int) -> Bool {
        if !isFull {
            array[writeIndex % array.count] = element
            writeIndex += 1
            
            return true
        } else {
            return false
        }
    }
    
    mutating func read() -> Int? {
        if !isEmpty {
            let element = array[readIndex % array.count]
            readIndex += 1
            
            return element
        } else {
            return nil
        }
    }
}


struct Queue {
    private var ringBuffer: RingBuffer
    
    init(count: Int) {
        ringBuffer = RingBuffer(count: count)
    }
    
    var isEmpty: Bool {
        ringBuffer.isEmpty
    }
    
    var peek: Int? {
        ringBuffer.first
    }
    
    @discardableResult
    mutating func enqueue(_ element: Int) -> Bool {
        ringBuffer.write(element)
    }
    
    mutating func dequeue() -> Int? {
        ringBuffer.read()
    }
}
             
let testCase = readLine()!.components(separatedBy: " ").map { Int($0)! }

let N = testCase[0]
let M = testCase[1]

var graph = [[Int]](repeating: [Int](), count: N + 1)
var inDegree = [Int](repeating: 0, count: N + 1)
var queue = Queue(count: N)
var order: [Int] = []

for _ in 0..<M {
    let testCase = readLine()!.components(separatedBy: " ").map { Int($0)! }
    
    // 앞에 서야 한다. 즉, 하나의 간선으로 연결된 다음 노드
    let parent = testCase[0]
    let child = testCase[1]
    
    graph[parent].append(child)
    inDegree[child] += 1
}

// 진입 차수가 0인 노드 큐에 추가
for i in 1..<inDegree.count {
    if inDegree[i] == 0 {
        queue.enqueue(i)
    }
}

// BFS 수행
while !queue.isEmpty {
    let node = queue.dequeue()!
    order.append(node)
    
    for edge in graph[node] {
        inDegree[edge] -= 1
        if inDegree[edge] == 0 {
            queue.enqueue(edge)
        }
    }
}

print(order.map { String($0) }.joined(separator: " "))
  • 위 문제를 해결하다가 보니 입력할때 동시에 진입 차수를 추가할 수 있다는 생각이 들었고 해당 방법으로 문제를 해결하면, 문제 해결 속도를 좀 더 줄일 수 있다고 생각했다. But!! 별차이 없다. 생각해보니 (V + V) 이여서 그런가... 그런데 왜 다른분들의 코드와 시간 복잡도가 2배이상 차이가 나는걸까 
// MARK: 2. DFS를 사용하여 문제 해결
import Foundation
enum VisiteState {
    case unvisited, visiting, visited
}

var visited: [VisiteState] = []
var stack: [Int] = []
var hasCycle = false

func dfs(graph: [[Int]], node: Int) {
    // 방문 중일때 방문했을 경우 Cycle 발생
    if visited[node] == .visiting {
        hasCycle = true
        return
    }
    
    // 이미 방문한 node는 무시
    if visited[node] == .visited {
        return
    }
    
    visited[node] = .visiting
    
    for neighbor in graph[node] {
        dfs(graph: graph, node: neighbor)
        if hasCycle { return }
    }
    
    visited[node] = .visited
    // 방문이 다 종료되면 Stack에 Node 추가
    stack.append(node)
}

func topologicalSort(graph: [[Int]], vertices: Int) -> [Int]? {
    visited = [VisiteState](repeating: .unvisited, count: vertices)
    stack = []
    hasCycle = false
    
    // 모든 노드에 대해서 dfs 실행
    for i in 1..<vertices {
        if visited[i] == .unvisited {
            dfs(graph: graph, node: i)
            if hasCycle { return nil }
        }
    }
    
    return stack.reversed()
}

let testCase = readLine()!.components(separatedBy: " ").map { Int($0)! }

let N = testCase[0]
let M = testCase[1]

var graph = [[Int]](repeating: [Int](), count: N + 1)

for _ in 0..<M {
    let testCase = readLine()!.components(separatedBy: " ").map { Int($0)! }
    
    // 앞에 서야 한다. 즉, 하나의 간선으로 연결된 다음 노드
    let parent = testCase[0]
    let child = testCase[1]
    
    graph[parent].append(child)
}

if let sorted = topologicalSort(graph: graph, vertices: N + 1) {
    print(sorted.map { String($0) }.joined(separator: " "))
}

문제집 - 백준 1766 G2

문제

  • 민오는 1번부터 N번까지 총 N개의 문제로 되어 있는 문제집을 풀려고 한다. 문제는 난이도 순서로 출제되어 있다. 즉 1번 문제가 가장 쉬운 문제이고 N번 문제가 가장 어려운 문제가 된다.
  • 어떤 문제부터 풀까 고민하면서 문제를 훑어보던 민오는, 몇몇 문제들 사이에는 '먼저 푸는 것이 좋은 문제'가 있다는 것을 알게 되었다. 예를 들어 1번 문제를 풀고 나면 4번 문제가 쉽게 풀린다거나 하는 식이다. 민오는 다음의 세 가지 조건에 따라 문제를 풀 순서를 정하기로 하였다.
  1. N개의 문제는 모두 풀어야 한다.
  2. 먼저 푸는 것이 좋은 문제가 있는 문제는, 먼저 푸는 것이 좋은 문제를 반드시 먼저 풀어야 한다.
  3. 가능하면 쉬운 문제부터 풀어야 한다.
  • 예를 들어서 네 개의 문제가 있다고 하자. 4번 문제는 2번 문제보다 먼저 푸는 것이 좋고, 3번 문제는 1번 문제보다 먼저 푸는 것이 좋다고 하자. 만일 4-3-2-1의 순서로 문제를 풀게 되면 조건 1과 조건 2를 만족한다. 하지만 조건 3을 만족하지 않는다. 4보다 3을 충분히 먼저 풀 수 있기 때문이다. 따라서 조건 3을 만족하는 문제를 풀 순서는 3-1-4-2가 된다.
  • 문제의 개수와 먼저 푸는 것이 좋은 문제에 대한 정보가 주어졌을 때, 주어진 조건을 만족하면서 민오가 풀 문제의 순서를 결정해 주는 프로그램을 작성하시오.

입력

  • 첫째 줄에 문제의 수 N(1 ≤ N ≤ 32,000)과 먼저 푸는 것이 좋은 문제에 대한 정보의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 둘째 줄부터 M개의 줄에 걸쳐 두 정수의 순서쌍 A,B가 빈칸을 사이에 두고 주어진다. 이는 A번 문제는 B번 문제보다 먼저 푸는 것이 좋다는 의미이다.
  • 항상 문제를 모두 풀 수 있는 경우만 입력으로 주어진다.

출력

  • 첫째 줄에 문제 번호를 나타내는 1 이상 N 이하의 정수들을 민오가 풀어야 하는 순서대로 빈칸을 사이에 두고 출력한다.

예제 입력 1 

4 2
4 2
3 1

예제 출력 1 

3 1 4 2

풀이

  • 최초 예제만 확인했을 때 0번째만 나눠서 queue에 값을 추가하고 0번째가 들어올 때 while문을 수행하는 식으로 하면 해결될 줄 알았다.
  • 하지만, 위와같이 하면 if문 안에서 while 중 0이 나오고 Degree가 for문 돌때 0을 또 만나면 값이 추가될 수 있어서 문제가 있다.
  • 같은 차수에서 여러개의 숫자가 들어올때에도 정렬이 필요하다는 것을 알았고, 해당 부분을 어떻게 정렬해줄까 고민하다가 우선순위 큐가 생각났다.
  • queue에 추가가 되는 방식이 차수가 0 이면 추가가 된다. 즉, 이는 앞서 들어온 숫자 또는 같은 차수에서 들어온 숫자들만 있다는 뜻이다.
  • queue에서 enqueue되는 시점에 2번 까지의 조건을 해결했고, queue에 들어오면서 3번의 조건을 달성해야 하기 때문에 queue를 오름차순 정렬 우선순위 큐로 만들면 문제를 해결할 수 있다. 
import Foundation

struct Heap {
    var elements: [Int] = []
    
    let sort: (Int, Int) -> Bool
    
    init(sort: @escaping (Int, Int) -> Bool, elements: [Int] = [] ) {
        self.sort = sort
        self.elements = elements
        
        if !elements.isEmpty {
            for i in stride(from: count / 2 - 1, through: 0, by: -1) {
                siftDown(from: i)
            }
        }
    }
    
    var isEmpty: Bool {
        elements.isEmpty
    }
    
    var count: Int {
        elements.count
    }
    
    func peek() -> Int? {
        elements.first
    }
    
    func leftChildIndex(ofParentAt index: Int) -> Int {
        (index * 2) + 1
    }
    
    func rightChildIndex(ofParentAt index: Int) -> Int {
        (index * 2) + 2
    }
    
    func parentIndex(ofChildAt index: Int) -> Int {
        (index - 1) / 2
    }
    
    private mutating func siftDown(from index: Int) {
        var parent = index
        
        while true {
            let left = leftChildIndex(ofParentAt: parent)
            let right = rightChildIndex(ofParentAt: parent)
            var candidate = parent
            
            if left < count && sort(elements[left], elements[candidate]) {
                candidate = left
            }
        
            if right < count && sort(elements[right], elements[candidate]) {
                candidate = right
            }
            
            if candidate == parent {
                return
            }
            elements.swapAt(parent, candidate)
            parent = candidate
        }
    }
    
    private mutating func siftUp(from index: Int) {
        var child = index
        var parent = parentIndex(ofChildAt: child)
        while child > 0 && sort(elements[child], elements[parent]) {
            elements.swapAt(child, parent)
            child = parent
            parent = parentIndex(ofChildAt: child)
        }
    }
    
    mutating func remove() -> Int? {
        guard !isEmpty else {
            return nil
        }
        elements.swapAt(0, count - 1)
        defer {
            siftDown(from: 0)
        }
        return elements.removeLast()
    }
    
    mutating func insert(_ element: Int) {
        elements.append(element)
        siftUp(from: elements.count - 1)
    }
}


struct Queue {
    private var heap: Heap

    init(sort: @escaping (Int, Int) -> Bool, elements: [Int] = []) {
        heap = Heap(sort: sort, elements: elements)
    }
    
    var isEmpty: Bool {
        heap.isEmpty
    }
    
    var peek: Int? {
        heap.peek()
    }
    
    @discardableResult
    mutating func enqueue(_ element: Int) -> Bool {
        heap.insert(element)
        return true
    }
    
    mutating func dequeue() -> Int? {
        heap.remove()
    }
}

func topologicalSortKahn(graph: [[Int]], vertices: Int) -> [Int] {
    var inDegree = [Int](repeating: 0, count: vertices)
    var queue = Queue(sort: <, elements: [Int]() )
    var order: [Int] = []
    
    for node in graph {
        for edge in node {
            inDegree[edge] += 1
        }
    }
    
    for i in 1..<inDegree.count {
        if inDegree[i] == 0 {
            queue.enqueue(i)
        }
    }
    
    while !queue.isEmpty {
        let node = queue.dequeue()!
        order.append(node)
        
        for edge in graph[node] {
            inDegree[edge] -= 1
            if inDegree[edge] == 0 {
                queue.enqueue(edge)
            }
        }
    }
    
    return order
}

let testCase = readLine()!.components(separatedBy: " ").map { Int($0)! }

let N = testCase[0]
let M = testCase[1]

var graph = [[Int]](repeating: [Int](), count: N + 1)

for _ in 0..<M {
    let testCase = readLine()!.components(separatedBy: " ").map { Int($0)! }
    
    // 앞에 서야 한다. 즉, 하나의 간선으로 연결된 다음 노드
    let parent = testCase[0]
    let child = testCase[1]
    
    graph[parent].append(child)
}

let sorted = topologicalSortKahn(graph: graph, vertices: N + 1)

print(sorted.map { String($0) }.joined(separator: " "))

최종 순위 - 백준 3665 G1

문제

  • 올해 ACM-ICPC 대전 인터넷 예선에는 총 n개의 팀이 참가했다. 팀은 1번부터 n번까지 번호가 매겨져 있다. 놀랍게도 올해 참가하는 팀은 작년에 참가했던 팀과 동일하다.
  • 올해는 인터넷 예선 본부에서는 최종 순위를 발표하지 않기로 했다. 그 대신에 작년에 비해서 상대적인 순위가 바뀐 팀의 목록만 발표하려고 한다. (작년에는 순위를 발표했다) 예를 들어, 작년에 팀 13이 팀 6 보다 순위가 높았는데, 올해 팀 6이 팀 13보다 순위가 높다면, (6, 13)을 발표할 것이다.
  • 창영이는 이 정보만을 가지고 올해 최종 순위를 만들어보려고 한다. 작년 순위와 상대적인 순위가 바뀐 모든 팀의 목록이 주어졌을 때, 올해 순위를 만드는 프로그램을 작성하시오. 하지만, 본부에서 발표한 정보를 가지고 확실한 올해 순위를 만들 수 없는 경우가 있을 수도 있고, 일관성이 없는 잘못된 정보일 수도 있다. 이 두 경우도 모두 찾아내야 한다.

입력

  • 첫째 줄에는 테스트 케이스의 개수가 주어진다. 테스트 케이스는 100개를 넘지 않는다. 각 테스트 케이스는 다음과 같이 이루어져 있다.
    • 팀의 수 n을 포함하고 있는 한 줄. (2 ≤ n ≤ 500)
    • n개의 정수 ti를 포함하고 있는 한 줄. (1 ≤ ti ≤ n) ti는 작년에 i등을 한 팀의 번호이다. 1등이 가장 성적이 높은 팀이다. 모든 ti는 서로 다르다.
    • 상대적인 등수가 바뀐 쌍의 수 m (0 ≤ m ≤ 25000)
    • 두 정수 ai와 bi를 포함하고 있는 m줄. (1 ≤ ai < bi ≤ n) 상대적인 등수가 바뀐 두 팀이 주어진다. 같은 쌍이 여러 번 발표되는 경우는 없다.

출력

  • 각 테스트 케이스에 대해서 다음을 출력한다.
    • n개의 정수를 한 줄에 출력한다. 출력하는 숫자는 올해 순위이며, 1등팀부터 순서대로 출력한다. 만약, 확실한 순위를 찾을 수 없다면 "?"를 출력한다. 데이터에 일관성이 없어서 순위를 정할 수 없는 경우에는 "IMPOSSIBLE"을 출력한다.

예제 입력 1 

3
5
5 4 3 2 1
2
2 4
3 4
3
2 3 1
0
4
1 2 3 4
3
1 2
3 4
2 3

예제 출력 1 

5 3 2 4 1
2 3 1
IMPOSSIBLE

풀이

  • 최초 문제 해결에 대해서 감이 안 잡혔다. 그 예로 당시 3번째 예제의 정답이 IMPOSSIBLE이라는 것을 이해를 못하고 있었는데, 문제를 다시 읽어보다가 이는 간선이 5 -> 4 -> 3 -> 2 -> 1 이렇게가 아니라 5 -> (4,3,2,1), 4 -> (3,2,1), 3 -> (2,1), 2 -> (1) 이렇게 라는 것을 깨닫게 되었다.
  • 이러한 그래프에서 변경된 순위에 대해서 방향을 바꿔주면 된다.

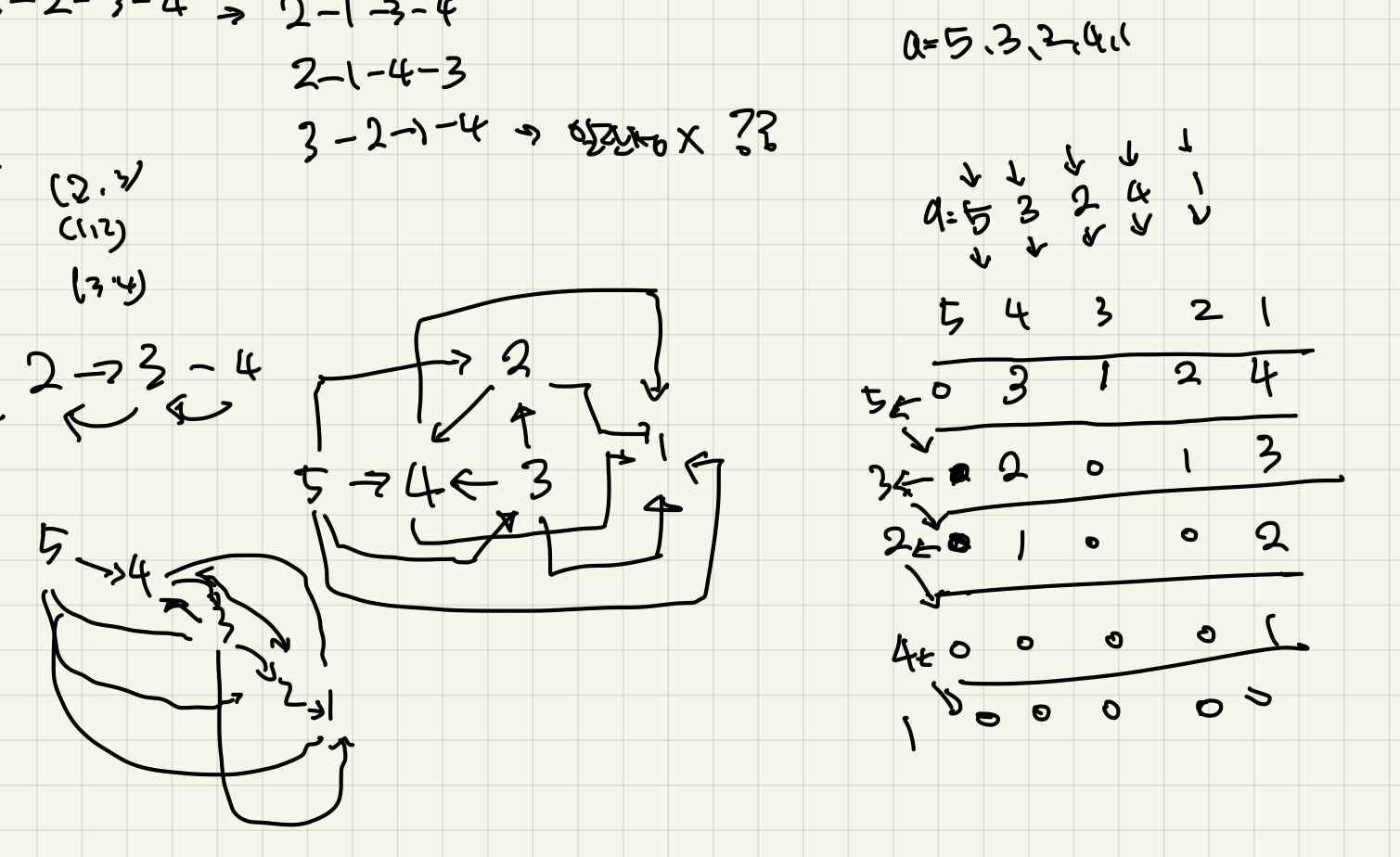
  • 주어진 위상 정렬에서 문제를 위한 올해 순위 예상 그래프를 만들고 나서 해당 그래프를 위상정렬을 다시 실시 해주면 되는데,
  • 여기서 위상 정렬이 정상적으로 수행된다면 해당 결과 값을 출력해주고,
  • 결과 값이 Cycle이 돌게된다면, IMPOSSIBLE을 출력해주면 된다.
  • 마지막으로 같은 node의 edges들이 0이 되는게 2개 이상일 경우 정확한 순위를 알 수 없기 때문에 ? 을 출력해주면 된다.
import Foundation

// Ring Buffer를 활용한 Queue
struct RingBuffer {
    private var array: [Int?]
    private var readIndex = 0
    private var writeIndex = 0
    
    init(count: Int) {
        array = Array(repeating: nil, count: count)
    }
    
    var first: Int? {
        array[readIndex]
    }
    
    private var availableSpaceForReading: Int {
        writeIndex - readIndex
    }
    
    private var availableSpaceForWriting: Int {
        array.count - availableSpaceForReading
    }
    
    var isEmpty: Bool {
        availableSpaceForReading == 0
    }
    
    var isFull: Bool {
        availableSpaceForWriting == 0
    }
    
    @discardableResult
    mutating func write(_ element: Int) -> Bool {
        if !isFull {
            array[writeIndex % array.count] = element
            writeIndex += 1
            
            return true
        } else {
            return false
        }
    }
    
    mutating func read() -> Int? {
        if !isEmpty {
            let element = array[readIndex % array.count]
            readIndex += 1
            
            return element
        } else {
            return nil
        }
    }
}


struct Queue {
    private var ringBuffer: RingBuffer
    
    init(count: Int) {
        ringBuffer = RingBuffer(count: count)
    }
    
    var isEmpty: Bool {
        ringBuffer.isEmpty
    }
    
    var peek: Int? {
        ringBuffer.first
    }
    
    @discardableResult
    mutating func enqueue(_ element: Int) -> Bool {
        ringBuffer.write(element)
    }
    
    mutating func dequeue() -> Int? {
        ringBuffer.read()
    }
}

func topologicalSortKahn(graph: [[Int]], vertices: Int) {
    var inDegree = [Int](repeating: 0, count: vertices)
    var queue = Queue(count: vertices - 1)
    var order: [Int] = []
    
    // 진입 차수 계산
    for node in graph {
        for edge in node {
            inDegree[edge] += 1
        }
    }
    
    // 진입 차수가 0인 노드 큐에 추가
    for i in 1..<inDegree.count {
        if inDegree[i] == 0 {
            queue.enqueue(i)
        }
    }
    
    // BFS 수행
    while !queue.isEmpty {
        let node = queue.dequeue()!
        order.append(node)
        
        var isCertain = 0
        
        for edge in graph[node] {
            inDegree[edge] -= 1
            if inDegree[edge] == 0 {
                isCertain += 1
                
                if isCertain > 1 {
                    print("?")
                    return
                }
                queue.enqueue(edge)
            }
        }
    }
        
    // 모든 노드가 처리되었는지 확인
    // 즉 큐가 조기 종료되면 order count가 vertices와 다름
    if order.count == vertices - 1 {
        print(order.map { String($0) }.joined(separator: " "))
        return
    } else {
        print("IMPOSSIBLE")
        return
    }
}

// 테스트 케이스 수
let N = Int(readLine()!)!

for _ in 0..<N {
    // 팀원 수
    let M = Int(readLine()!)!
        
    // 팀원 배열
    let testCase = [0] + readLine()!.components(separatedBy: " ").map { Int($0)! }
    
    var graph = [[Int]](repeating: [Int](), count: M + 1)
    
    // 그래프 초기화
    for (index, value) in testCase.enumerated() {
        guard index > 0 else { continue }
        guard index + 1 <= M else { continue }
        
        for i in (index + 1)...M {
            graph[value].append(testCase[i])
        }
    }
     
    let thisYear = Int(readLine()!)!
    
    for _ in 0..<thisYear {
        let testCase2 = readLine()!.components(separatedBy: " ").map { Int($0)! }
        
        let node1 = testCase2[0]
        let node2 = testCase2[1]
        
        if graph[node1].contains(node2) {
            graph[node1] = graph[node1].filter { $0 != node2 }
            graph[node2].append(node1)
        } else if graph[node2].contains(node1) {
            graph[node2] = graph[node2].filter { $0 != node1 }
            graph[node1].append(node2)
        }
    }
    topologicalSortKahn(graph: graph, vertices: M + 1)
}

출처(참고문헌)

제가 학습한 내용을 요약하여 정리한 것입니다. 내용에 오류가 있을 수 있으며, 어떠한 피드백도 감사히 받겠습니다.

감사합니다.

profile
전성훈
이전 포스트

[Data Structure / Algorithms] Methods for Finding a MST(Minimum Spannig Tree) - Kruskal & Prim

다음 포스트

[Data Structure / Algorithms] Two Pointer

0개의 댓글