KMP 알고리즘

KMP 알고리즘은 대표적인 문자열 매칭 알고리즘이다.

📝 정의

기본적으로 문자열 매칭 알고리즘이란 특정한 글이 있을 때 그 글 안에서 하나의 문자열을 찾는 알고리즘이다.
이는, 우리가 크롬에나 파폭에서 ctrl + f 를 눌러 글자 찾기에도 해당 알고리즘이 다 들어가 있는 것이다.

그럼 우선 KMP 알고리즘에 대해 알아보기 전에 간단한 단순 비교 문자열 매칭 알고리즘 에 대해 알아보자.

단순 비교 문자열 매칭 알고리즘

우선 단순 비교 문자열 매칭 알고리즘 에 대해 알아보자면, 단순 비교 알고리즘 은 말 그대로 하나씩 확인하는 알고리즘으로 가장 간단한 형태의 알고리즘이다.

이렇게 각 노드를 돌며 각각의 요소가 맞는지를 확인하는 작업을 반복적으로 거쳐 동일한 문자열을 찾는다.
이는 O(N*M) 의 시간 복잡도를 갖는다. 효율적이진 않지만 코드는 그냥 for 문 돌리면 돼서 작성은 쉽다.

🛠 특징

만약 우리가 단순 비교 문자열 매칭 알고리즘 방법처럼 모든 경우를 다 비교하는 경우의 최악의 경우의 수는 굉장히 크다. 따라서 모든 경우를 다 비교하지 않아도 부분 문자열을 찾을 수 있는 KMP 알고리즘은

접두사와 접미사의 개념을 활용하여 반복되는 연산을 얼마나 줄일 수 있는지 를 판별하여 매칭할 문자열을 빠르게 점프하는 기법이다.
이는 반대로 실패함수를 작성하여 실패지점을 파악 후 얼마나 점프할 수 있는지를 접두사와 접미사를 활용하여 찾는 것이다.
이제 예를 들어 알아보자.

⚙ 동작

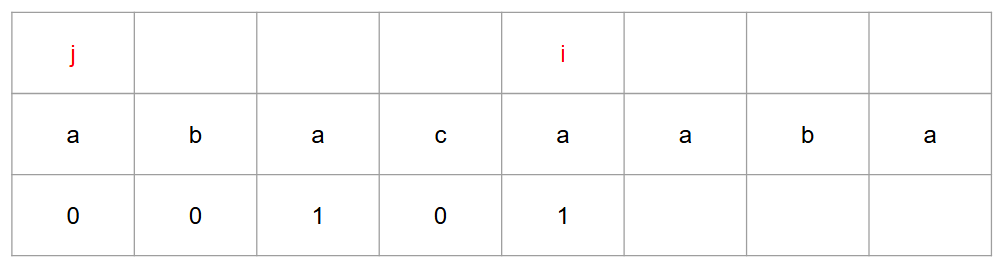
abacaaba 라는 문자열에서 접두사와 접미사를 찾아보자면 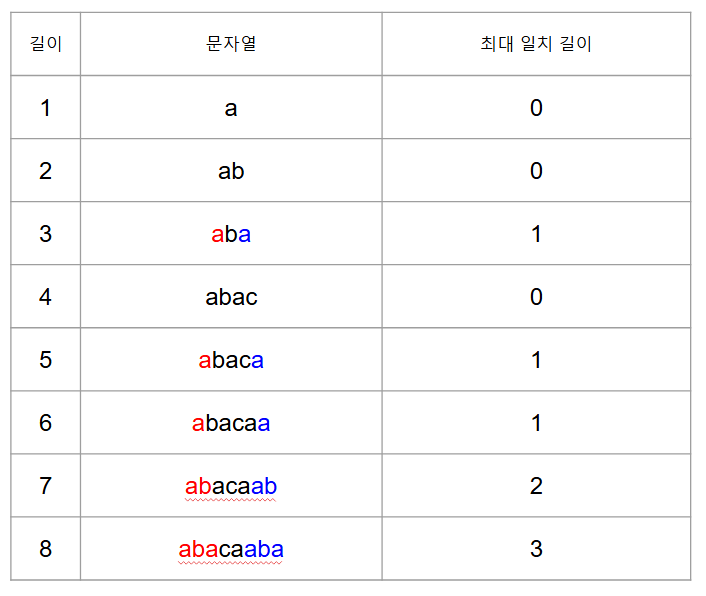다음과 같은 과정으로 도출할 수 있다.

이제 하나하나 살펴보고 이를 코드로 옮겨보자.

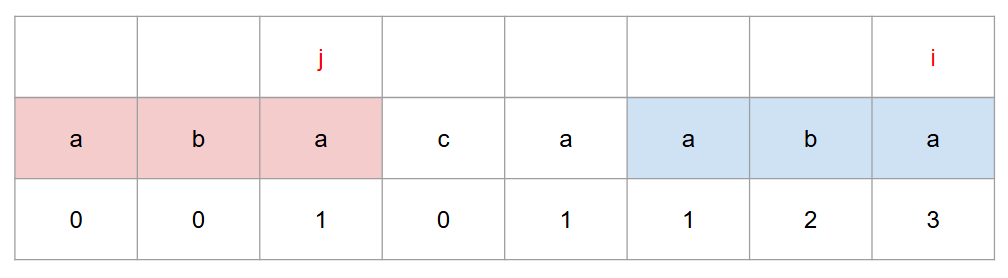
1. j 와 i 가 가르키는 값이 일치하면 j 의 숫자에서 +1 을 넣어준다.
   

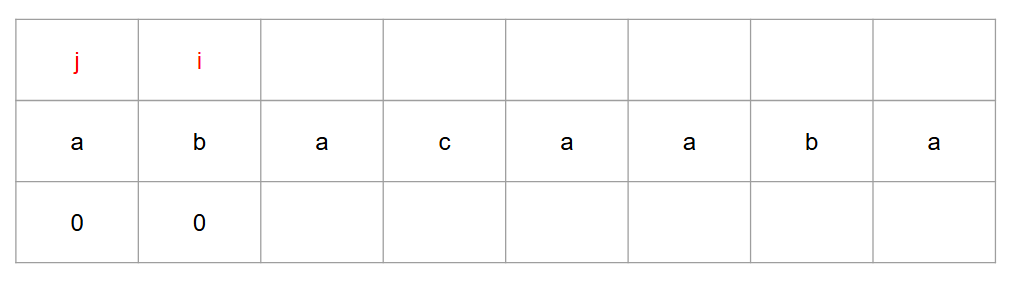
2. 일치하지 않다면 j 에서 1을 뺀 인덱스로 이동 후 i 를 1 증가시킨다.
   

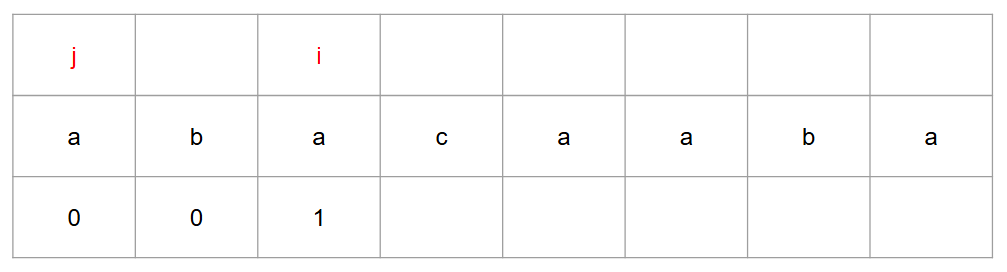
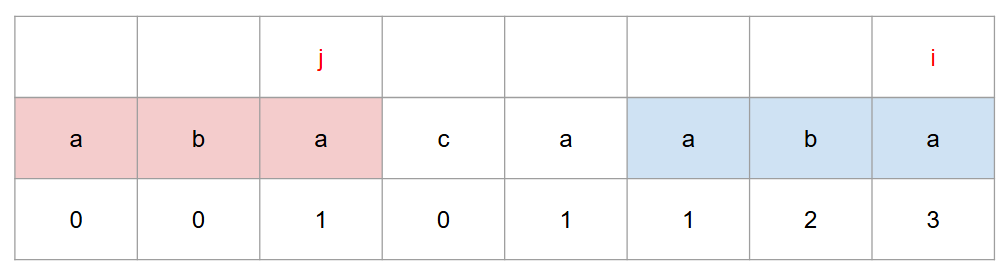
3. 만약 일치하다면 i, j 모두 1 증가시킨다.
   

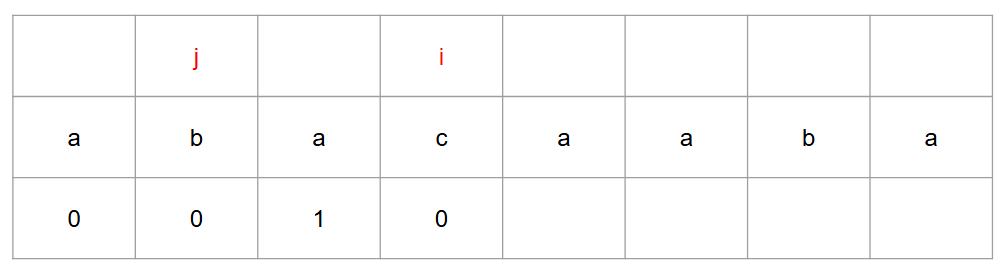
4. 이제 이를 반복한다.

public class Test {
    public static void main(String[] args) throws IOException {
        String pattern = "abacaaba";
        int[] answer = mkTable(pattern);
        System.out.println(Arrays.toString(answer));
    }

    private static int[] mkTable(String pattern) {
        char[] a = pattern.toCharArray();
        int patternSize = a.length;
        int[] table = new int[patternSize];
        int j = 0;
        for (int i = 1; i < patternSize; i++) {
            while (j > 0 && a[i] != a[j]) {
                j--;
                table[i] = 0;
            }
            if (a[i] == a[j]) {
                table[i] = ++j;
            }
        }
        return table;
    }
}

이렇게 하면 접두사와 접미사를 늘려가며 비교하다가 일치하는 않은 경우가 발생하면 일치했던 부분까지 되돌아가서 다시 검사를 하는 방식으로 빠르게 "최대 일치 길이" 테이블을 구축할 수 있다.
이제 이렇게 최대 일치 길이 테이블을 구축한 뒤에는 다음과 같이 문자열 매칭을 수행할 수 있다.

자, 아래 부분에서 불일치가 발생하였다면,

j 의 -1 부분을 table 에서 가져오면 1 을 가져올 수 있다.

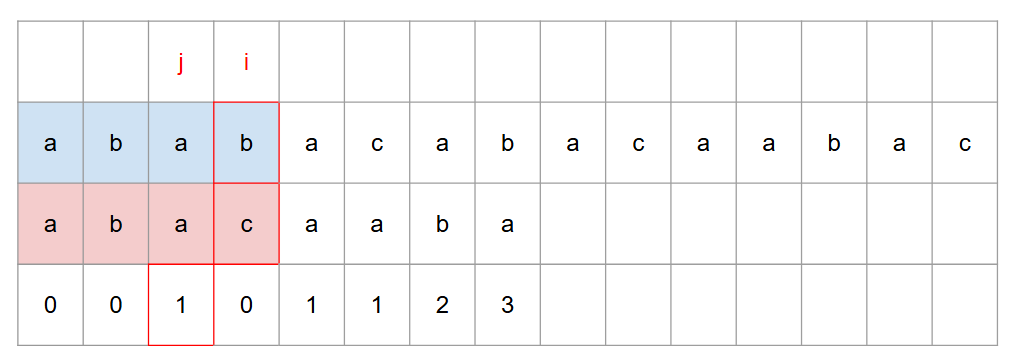
그리고 해당 인덱스의 pattern 까지는 parent 지점과 비교한다 (이떄 그 앞은 모두 일치한다고 가정한다. 왜? => table 에 약속을 정해두었으니까)

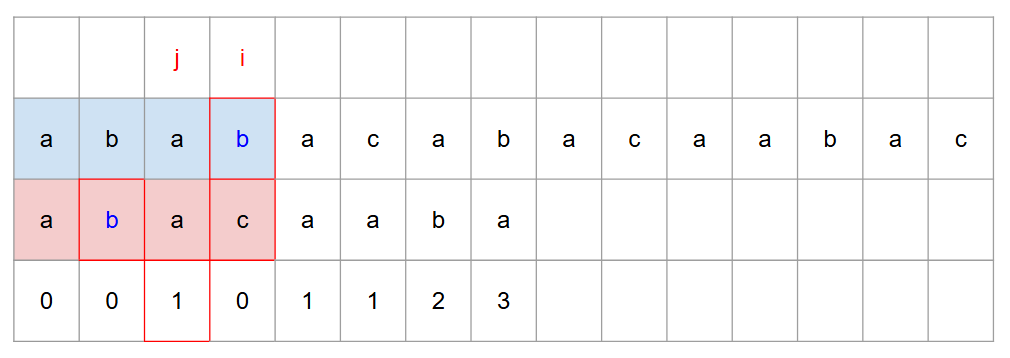
그래서 쭉 진행하다보면 또 틀린 부분을 마추치게된다.
이때, 앞서 했던 것 처럼 틀린 지점의 j-1 의 index 를 table 에서 찾고 해당 값 만큼 patter 과 parent 가 일치한다고 가정한다.

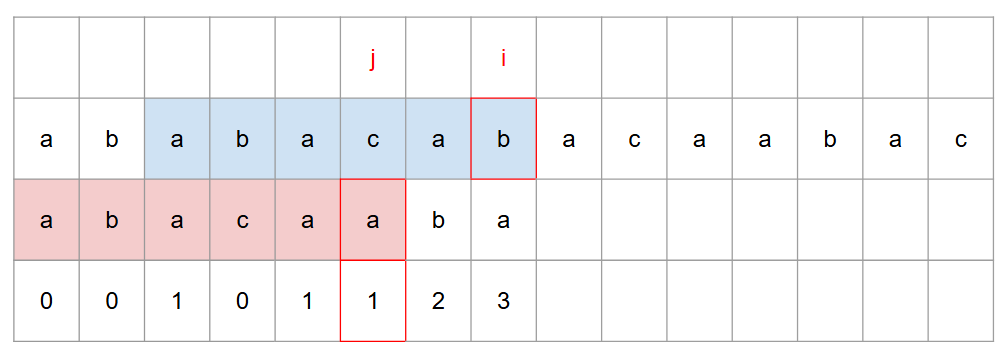
그러면 다음과 같이 동작이 된다.

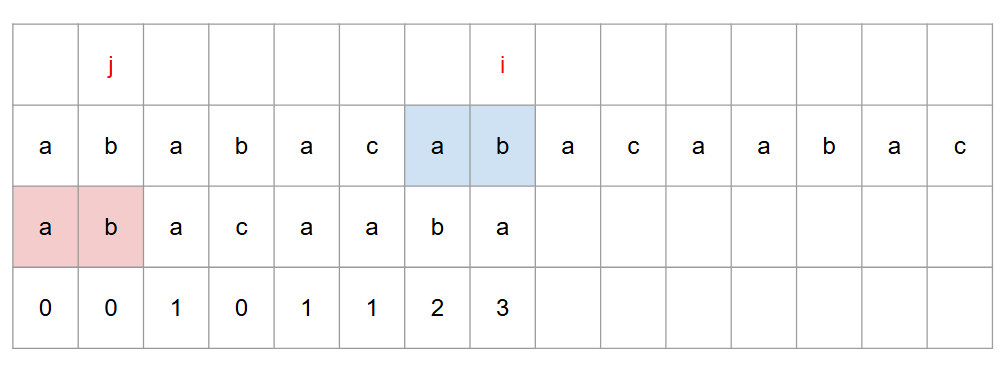
결과

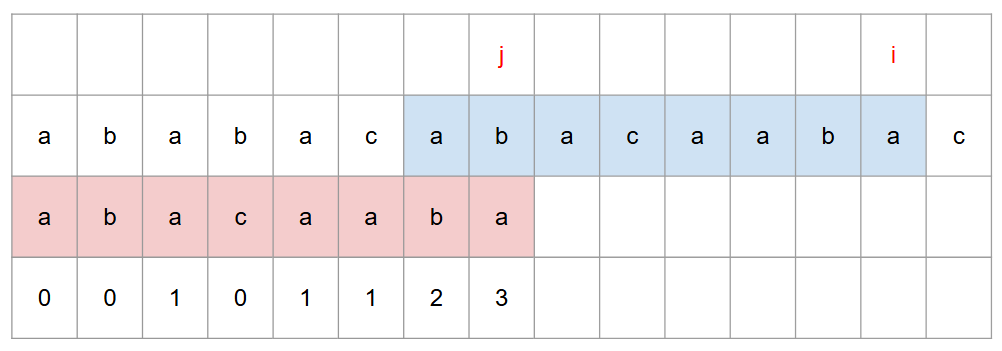
이를 코드로 옮기면 다음과 같다.

⏰시간 복잡도

💻 코드

import java.util.Arrays;

public class KMP {
    public static void KMPSearch(String parent, String pattern) {
        int[] table = mkTable(pattern);
        int parentSize = parent.length();
        int patternSize = pattern.length();

        int i = 0; // 부모의 인덱스
        int j = 0; // 패턴의 인덱스

        while (i < parentSize) {
            if (pattern.charAt(j) == parent.charAt(i)) {
                i++;
                j++;
            }

            if (j == patternSize) {
                System.out.println("패턴이 " + (i - patternSize + 1) + " 위치에서 발견됨");
                j = table[j - 1];
            } else if (i < parentSize && pattern.charAt(j) != parent.charAt(i)) {
                if (j != 0) {
                    j = table[j - 1];
                } else {
                    i++;
                }
            }
        }
    }

    private static int[] mkTable(String pattern) {
        int patternSize = pattern.length();
        int[] table = new int[patternSize];

        int j = 0;
        int i = 1;

        while (i < patternSize) {
            if (pattern.charAt(i) == pattern.charAt(j)) {
                j++;
                table[i] = j;
                i++;
            } else {
                if (j != 0) {
                    j = table[j - 1];
                } else {
                    table[i] = 0;
                    i++;
                }
            }
        }

        return table;
    }

    public static void main(String[] args) {
        String text = "ababacabacaabacaaba";
        String pattern = "abacaaba";
        int[] answer = mkTable(pattern);
        KMPSearch(text, pattern);
        System.out.println(Arrays.toString(answer));
    }
}