Bipartite Matching

네트워크 플로우와 연결된 개념인 이분 매칭 알고리즘에 대해 알아보자.

📝 정의

A 집단이 B 집단을 선택하는 방법에 대한 알고리즘이다.

🛠 특징

이분 매칭은 네트워크 플로우의 한 종류이다.

1. 회사 집단과 지원자 집단이 있다고 가정하자. 그리고 요구 사항이 다음과 같다고 가정할 때, 가장 많이 매칭해주는 방법을 찾는 것이 바로 이분 매칭 알고리즘이다.

• 이때 여기서 말하는 가장 많이 는 네트워크 플로우의 최대 유량과 동일한 의미를 갖는다.

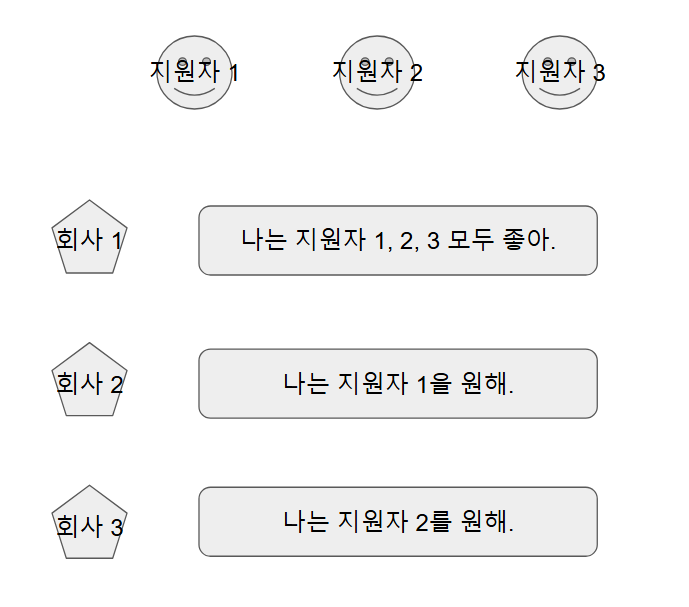
2. 다시 말해 효과적으로 매칭시켜준다는 뜻은 최대 매칭을 의미하는 것이고 이는 모든 회사 각각 지원자를 선택하여 최대한 많이 연결되는 경우를 찾는 문제라고 볼 수 있다. 대신 이제 각 용량이 1인 네트워크 플로우 문제라고 볼 수 있다.

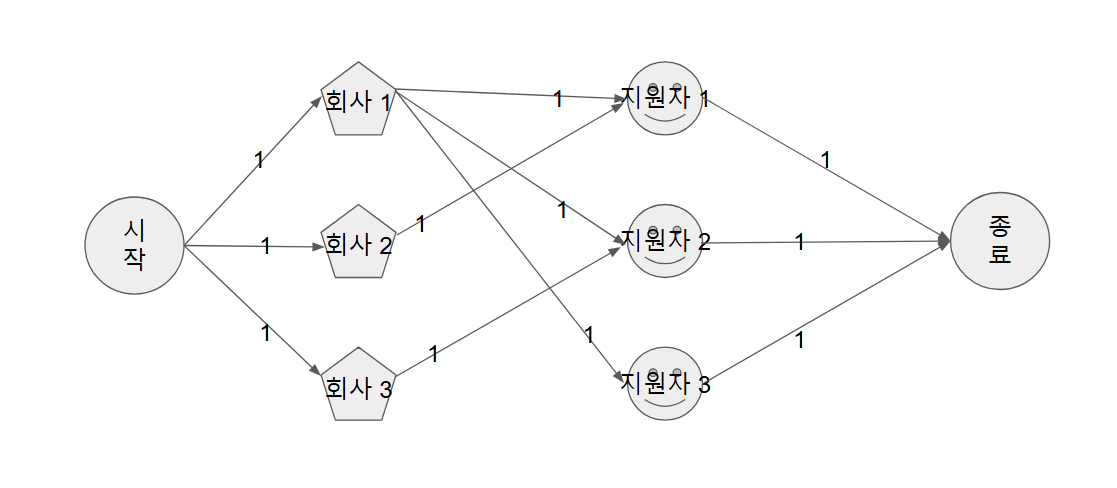
3. 이때 우리는 네트워크 플로우의 해결법 중 하나인 에드몬드 카프 알고리즘( O(V*E^2) ) 대신 이분 매칭에 한하여 더 빠르고 효율적인 DFS 로 문제를 해결할 수 있다.

⚙ 동작

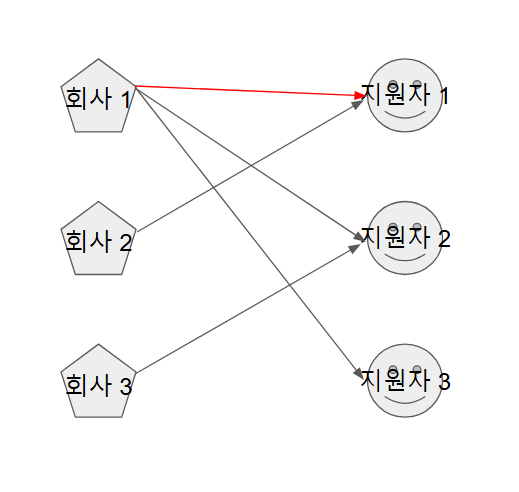
1. 회사 집단의 1번 노드가 선택지 중 1번을 선택
   

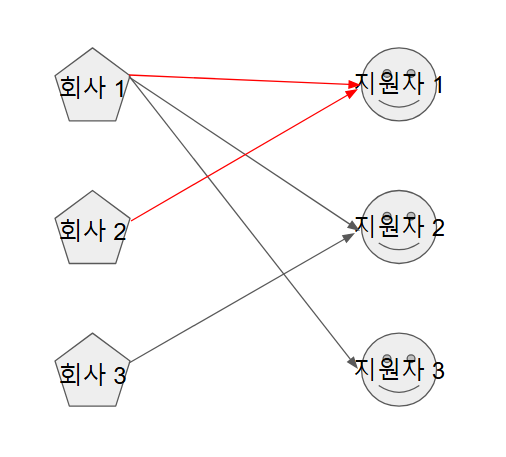
2. 회사 집단의 다음 노드가 선택지 중 1번을 선택
   

3. 충돌이 일어날 경우 앞선 노드가 선택지 중 다음 요소를 선택
   

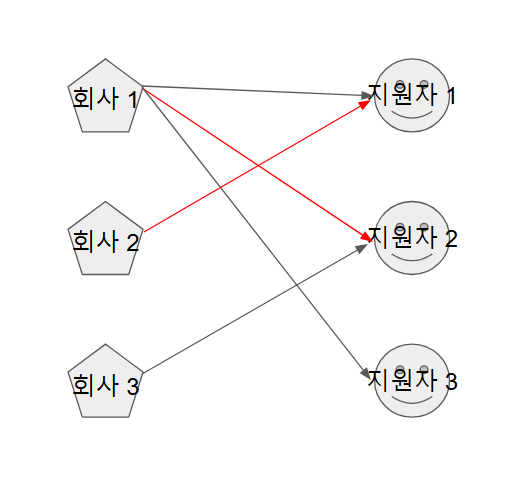
4. 회사 집단의 다음 노드가 선택지 중 1번을 선택
   

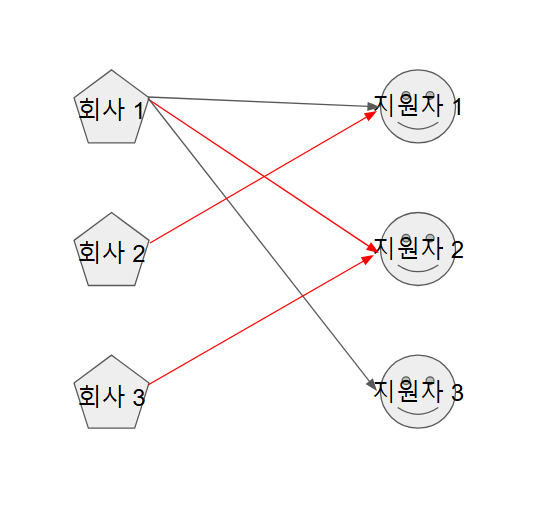
5. 다시 선택지 중 1번을 검토 => 지원자 1 을 선택한 회사 2 는 지원자 1 을 제외한 나머지 선택권이 없기 때문에 pass => 다음 요소를 선택
   

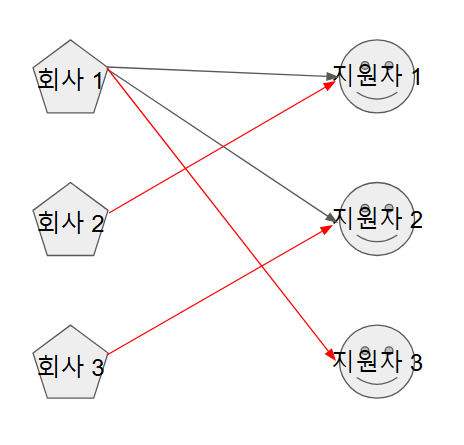
⏰시간 복잡도

앞서 말한대로 DFS 를 사용하여 이분 매칭 문제를 해결하게 된다면 O(V * E) 의 시간 복잡도를 갖게된다.
왜냐하면 총 DFS 는 정점의 개수 만큼 실행된다.

for (int u = 0; u < n; u++) {
  visited = new boolean[m];
  if (dfs(u)) {
    result++;
  }
}

그리고 해당 DFS 내에서 간선의 개수만큼 실행되기 때문에 V*E 의 시간 복잡도를 갖는 것이다.

for (int v : graph[u]) {
  // 이미 처리한 노드는 더이상 볼 필요가 없음.
  if (visited[v]) continue;
  visited[v] = true;

  // 비어있거나 점유 노드에 더 들어갈 공간이 있는 경우
  if (match[v] == -1 || dfs(match[v])) {
    match[v] = u;
    return true;
  }
}

💻 코드

import java.util.*;

public class BipartiteMatching {
    static List<Integer>[] graph;
    static int[] match;
    static boolean[] visited;

    public static void main(String[] args) {
        int n = 3, m = 3; // 왼쪽 그룹 크기(n), 오른쪽 그룹 크기(m)
        graph = new ArrayList[n];

        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }

        // 그래프 연결 (왼쪽 그룹 -> 오른쪽 그룹)
        graph[0].add(0);
        graph[0].add(1);
        graph[0].add(2);
        graph[1].add(0);
        graph[2].add(1);

        System.out.println("최대 매칭 개수: " + maxBipartiteMatching(n, m));
        System.out.println("매칭 결과: " + Arrays.toString(match));
    }

    public static int maxBipartiteMatching(int n, int m) {
        match = new int[m]; // 오른쪽 그룹의 매칭된 노드
        Arrays.fill(match, -1);
        int result = 0;

        for (int u = 0; u < n; u++) {
            visited = new boolean[m];
            if (dfs(u)) {
                result++;
            }
        }
        return result;
    }

    public static boolean dfs(int u) {
        // 연결된 모든 노드에 대해 들어갈 수 있는지 시도.
        for (int v : graph[u]) {
            // 이미 처리한 노드는 더이상 볼 필요가 없음.
            if (visited[v]) continue;
            visited[v] = true;

            // 비어있거나 점유 노드에 더 들어갈 공간이 있는 경우
            if (match[v] == -1 || dfs(match[v])) {
                match[v] = u;
                return true;
            }
        }
        return false;
    }
}