Three.js Geometries Core

강정우·2025년 1월 3일
three.js
0

three.js

목록 보기
6/24
post-thumbnail

Geometries

굉장히 다양한 기하들을 볼 수 있다. 박스 모양, 공 모양 등..
우선 대표적인 Box Geometry 를 보자.

BoxGeometry

const boxGeometry = new THREE.BoxGeometry()
const material = new THREE.MeshNormalMaterial({
    wireframe: true,
})
const cube = new THREE.Mesh(boxGeometry, material)
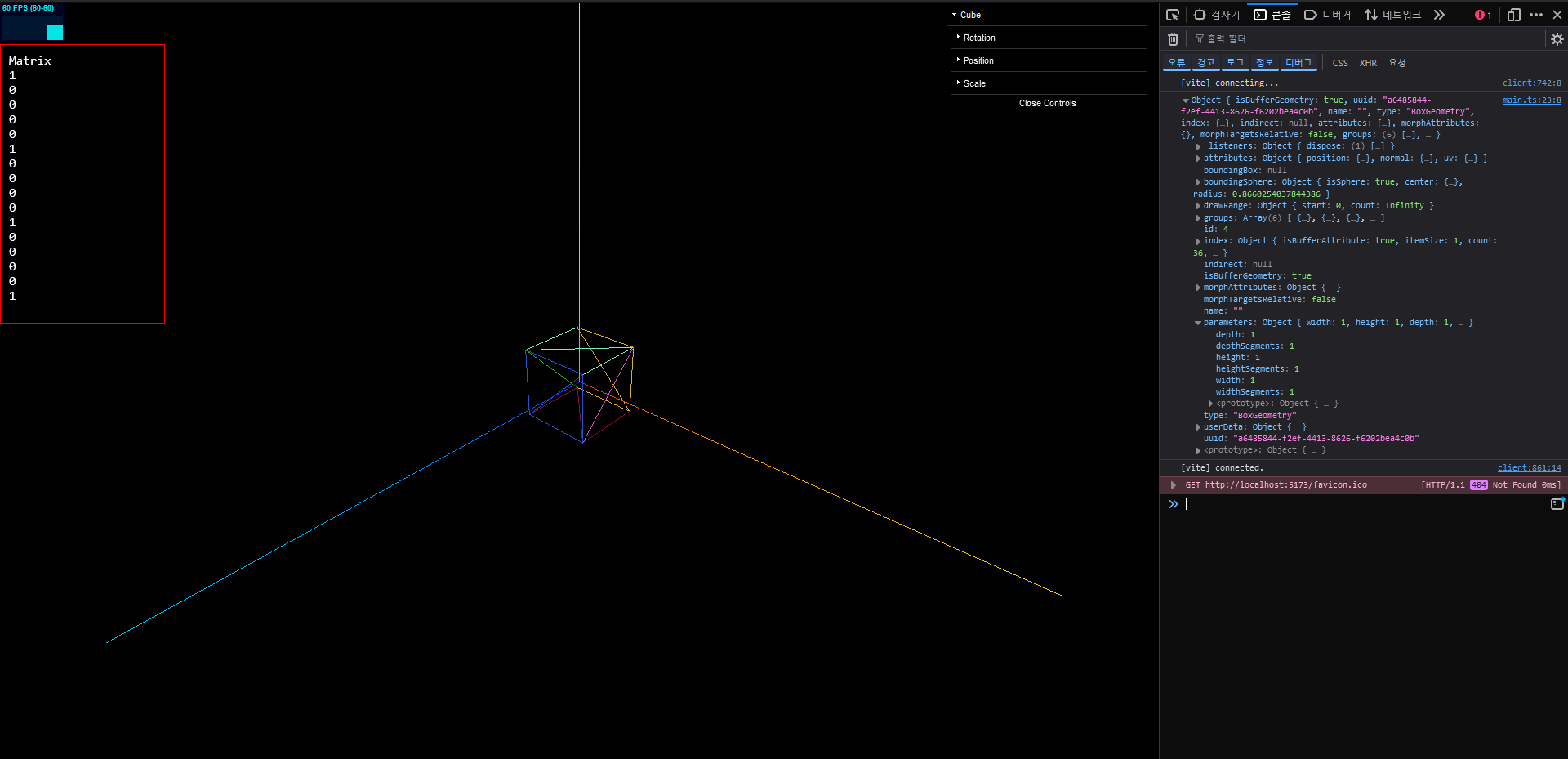
scene.add(cube)

위와 같은 코드를 작성한 후 로그를 찍어보면 parameters 에 BoxGeometry 의 생성자 속성값들을 설정할 수 있다.
또한 attributes 의 position 에 들어가보면 굉장히 많은 값들을 볼 수 있는데 이는 xyz 씩 하여 BoxGeometry의 각 점의 위치를 나타내고 있다.

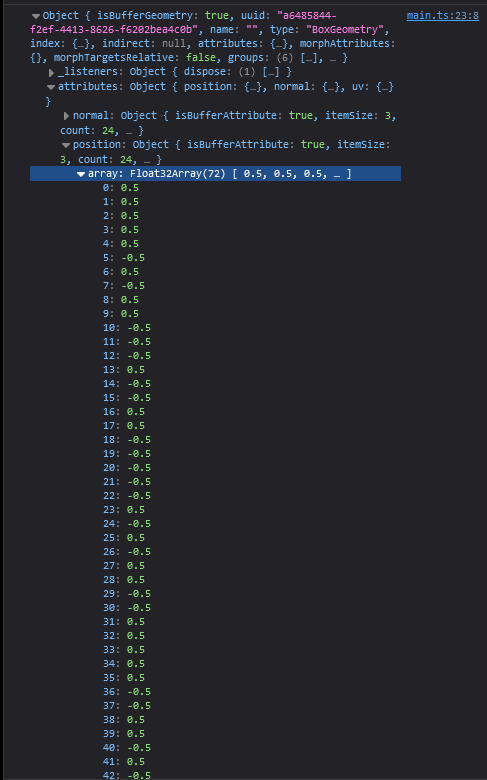
그리고 여기서부터 중요한거

const cubeFolder = gui.addFolder('Cube')
const cubeScaleFolder = cubeFolder.addFolder('Scale')
cubeScaleFolder.add(cube.scale, 'x', -5, 5, 0.1).onFinishChange(function() { console.log(cube.geometry) })
cubeScaleFolder.add(cube.scale, 'y', -5, 5, 0.1)
cubeScaleFolder.add(cube.scale, 'z', -5, 5, 0.1)

GUI에 Scale 을 변환한 후에 log 를 찍도록 코드를 수정한 후 로그를 보면 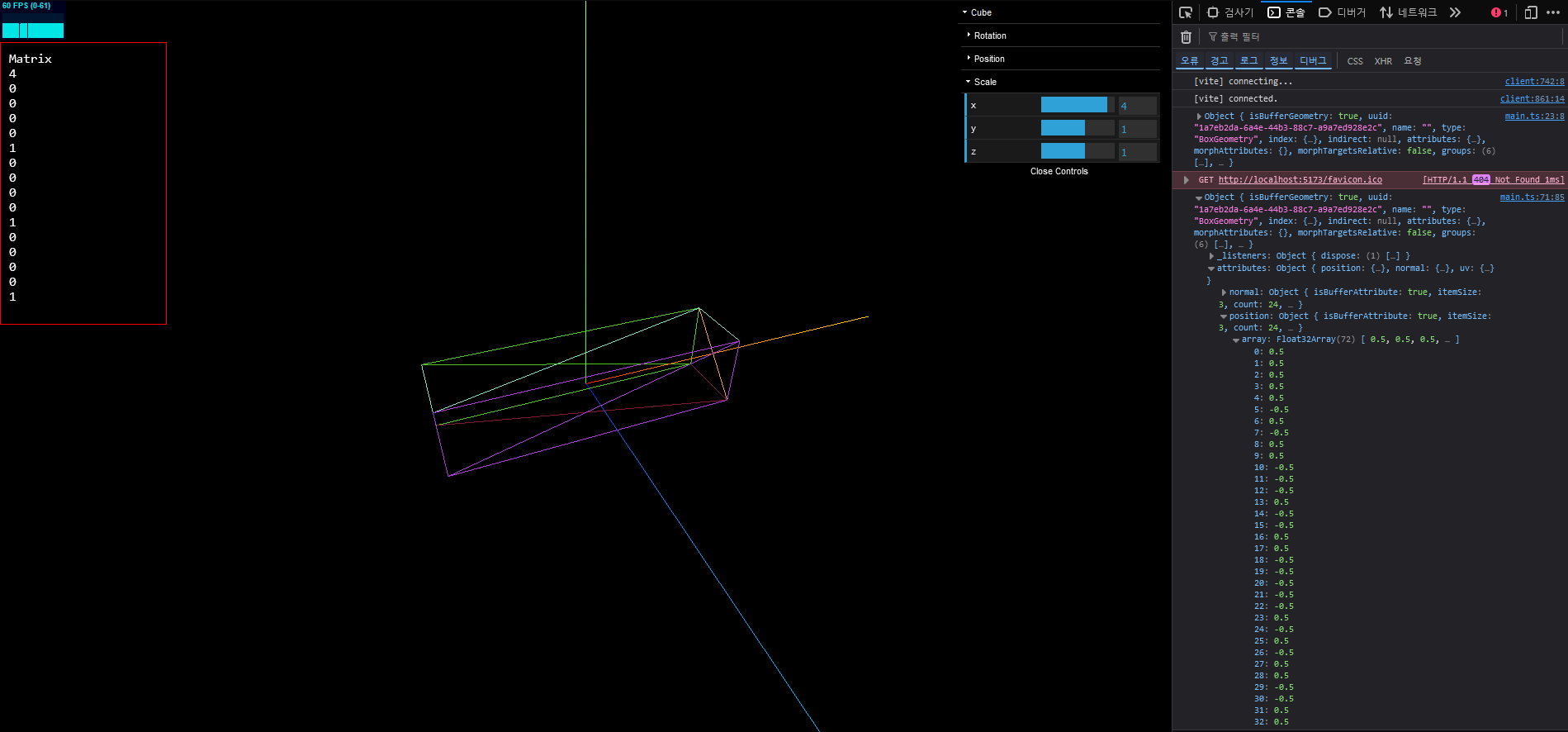놀랍게도 모든 position 값들이 그대로 존재한다. 왜일까?

정점 버퍼 데이터와 메시의 스케일 변환 방식

1. 스케일링의 동작 원리

cube.scale.x를 변경하면, Mesh의 변환 매트릭스(matrix)가 업데이트된다.
Three.js는 Mesh의 스케일을 변경하더라도, 기본 지오메트리의 정점 데이터(attributes.position)에는 영향을 미치지 않는다.
반면 스케일 변환은 렌더링 시점에 적용된다. 즉, BoxGeometry의 정점 데이터는 그대로 유지되고, 변환 매트릭스를 통해 스케일링 효과를 계산해 화면에 출력한다.

개념기본 지오메트리의 정점 데이터Object3D의 matrix 속성
주요 역할3D 모델의 형태를 정의하는 정점 위치 및 속성.객체의 위치, 회전, 스케일을 표현하는 변환 행렬.
구성 요소정점의 위치, 법선, 텍스처 좌표 등.4x4 행렬의 위치, 회전, 스케일 구성 요소.
변환 적용정점 데이터는 지역 좌표계에서 정의되며, 변환을 적용하기 위해 matrix와 곱셈이 필요함.정점 데이터를 지역 좌표계에서 월드 좌표계로 변환하는 데 사용됨.
자동 업데이트정점 데이터는 수동으로 수정해야 함.객체의 위치, 회전, 스케일 변경 시 자동으로 업데이트됨.
계산정점 간의 관계 및 형상을 정의하는 데 사용됨.객체의 변환을 계산하고 자식 객체에 영향을 미침.

2. geometry.attributes.position이 변하지 않는 이유

geometry.attributes.position은 정점 데이터를 저장하는 버퍼로, 초기화 시 한 번 생성되고 이후에는 직접 수정되지 않는다.
Mesh의 스케일을 변경해도 Three.js는 기본 지오메트리 데이터(BoxGeometry)를 업데이트하지 않는다.
대신 변환 매트릭스(Matrix4)를 통해 변형된 결과를 렌더링할 뿐이다.
따라서, 로그를 출력할 때 geometry.attributes.position의 값은 변경되지 않고 초기 상태를 유지하는 것이다.

3. 그렇다면 이 악물고 스케일링이 반영된 데이터를 확인하겠다면?

스케일링이 적용된 정점 데이터를 확인하려면, 메시의 변환 매트릭스를 정점 데이터에 직접 적용해야 한다. 

cubeScaleFolder.add(cube.scale, 'x', -5, 5, 0.1).onFinishChange(() => {
    // 원본 geometry를 복사하여 변환된 값을 계산
    const transformedPositions = cube.geometry.attributes.position.array.slice();
    const positionCount = cube.geometry.attributes.position.count;

    const matrix = cube.matrixWorld; // 메시의 월드 변환 매트릭스
    const vector = new THREE.Vector3();

    for (let i = 0; i < positionCount; i++) {
        vector.set(
            transformedPositions[i * 3],
            transformedPositions[i * 3 + 1],
            transformedPositions[i * 3 + 2]
        );

        vector.applyMatrix4(matrix); // 변환 매트릭스를 정점에 적용
        console.log(`Transformed Vertex ${i}:`, vector.toArray());
    }
});

그럼 왜 기본 데이터를 그대로 유지할까?
Three.js는 성능 최적화를 위해 원본 데이터를 변경하지 않는다.
왜냐하면 변경할 경우, GPU 메모리와 CPU 사이의 데이터를 다시 동기화해야 하며, 이는 성능 저하를 유발하기 때문이다.
따라서 Sclae, Rocation, Position 등은 모두 매트릭스 연산을 사용하여 효율적으로 처리되고, 정점 데이터(attributes.position)에는 영향을 미치지 않는다.

🖥 코드

따라서 위 Geometries 중 3가지를 골라서 작업하면 전체 코드는 아래와 같다.

import './style.css'
import * as THREE from 'three'
import { OrbitControls } from 'three/addons/controls/OrbitControls.js'
import Stats from 'three/addons/libs/stats.module.js'
import { GUI } from 'dat.gui'

const scene = new THREE.Scene()
scene.add(new THREE.AxesHelper(5))

const camera = new THREE.PerspectiveCamera(75, window.innerWidth / window.innerHeight, 0.1, 1000)
camera.position.set(-2, 4, 5)

const renderer = new THREE.WebGLRenderer()
renderer.setSize(window.innerWidth, window.innerHeight)
document.body.appendChild(renderer.domElement)

new OrbitControls(camera, renderer.domElement)

const boxGeometry = new THREE.BoxGeometry()
const sphereGeometry = new THREE.SphereGeometry()
const icosahedronGeometry = new THREE.IcosahedronGeometry()

const material = new THREE.MeshNormalMaterial({
    wireframe: true,
})

const cube = new THREE.Mesh(boxGeometry, material)
cube.position.x = -4
scene.add(cube)

const sphere = new THREE.Mesh(sphereGeometry, material)
sphere.position.x = 0
scene.add(sphere)

const icosahedron = new THREE.Mesh(icosahedronGeometry, material)
scene.add(icosahedron)
sphere.position.x = 4

window.addEventListener('resize', () => {
    camera.aspect = window.innerWidth / window.innerHeight
    camera.updateProjectionMatrix()
    renderer.setSize(window.innerWidth, window.innerHeight)
})

const stats = new Stats()
document.body.appendChild(stats.dom)

const gui = new GUI()

const cubeData = {
  width: 1,
  height: 1,
  depth: 1,
  widthSegments: 1,
  heightSegments: 1,
  depthSegments: 1
}

const cubeFolder = gui.addFolder('Cube')
const cubeRotationFolder = cubeFolder.addFolder('Rotation')
cubeRotationFolder.add(cube.rotation, 'x', 0, Math.PI * 2, 0.01)
cubeRotationFolder.add(cube.rotation, 'y', 0, Math.PI * 2, 0.01)
cubeRotationFolder.add(cube.rotation, 'z', 0, Math.PI * 2, 0.01)
const cubePositionFolder = cubeFolder.addFolder('Position')
cubePositionFolder.add(cube.position, 'x', -10, 10)
cubePositionFolder.add(cube.position, 'y', -10, 10)
cubePositionFolder.add(cube.position, 'z', -10, 10)
const cubeScaleFolder = cubeFolder.addFolder('Scale')
cubeScaleFolder.add(cube.scale, 'x', -5, 5, 0.1).onFinishChange(function() { console.log(cube.geometry) })
cubeScaleFolder.add(cube.scale, 'y', -5, 5, 0.1)
cubeScaleFolder.add(cube.scale, 'z', -5, 5, 0.1)

cubeFolder
  .add(cubeData, 'width', 1, 30)
  .onChange(regenerateBoxGeometry)
  .onFinishChange(function() { console.log(cube.geometry) })
cubeFolder.add(cubeData, 'height', 1, 30).onChange(regenerateBoxGeometry)
cubeFolder.add(cubeData, 'depth', 1, 30).onChange(regenerateBoxGeometry)
cubeFolder.add(cubeData, 'widthSegments', 1, 30).onChange(regenerateBoxGeometry)
cubeFolder.add(cubeData, 'heightSegments', 1, 30).onChange(regenerateBoxGeometry)
cubeFolder.add(cubeData, 'depthSegments', 1, 30).onChange(regenerateBoxGeometry)
cubeFolder.open()

function regenerateBoxGeometry() {
  const newGeometry = new THREE.BoxGeometry(
    cubeData.width,
    cubeData.height,
    cubeData.depth,
    cubeData.widthSegments,
    cubeData.heightSegments,
    cubeData.depthSegments
  )
  cube.geometry.dispose()
  cube.geometry = newGeometry
}

const sphereData = {
  radius: 1,
  widthSegments: 8,
  heightSegments: 6,
  phiStart: 0,
  phiLength: Math.PI * 2,
  thetaStart: 0,
  thetaLength: Math.PI
}
const sphereFolder = gui.addFolder('Sphere')
sphereFolder.add(sphereData, 'radius', 0.1, 30).onChange(regenerateSphereGeometry)
sphereFolder.add(sphereData, 'widthSegments', 1, 32).onChange(regenerateSphereGeometry)
sphereFolder.add(sphereData, 'heightSegments', 1, 16).onChange(regenerateSphereGeometry)
sphereFolder.add(sphereData, 'phiStart', 0, Math.PI * 2).onChange(regenerateSphereGeometry)
sphereFolder.add(sphereData, 'phiLength', 0, Math.PI * 2).onChange(regenerateSphereGeometry)
sphereFolder.add(sphereData, 'thetaStart', 0, Math.PI).onChange(regenerateSphereGeometry)
sphereFolder.add(sphereData, 'thetaLength', 0, Math.PI).onChange(regenerateSphereGeometry)
sphereFolder.open()

function regenerateSphereGeometry() {
  const newGeometry = new THREE.SphereGeometry(
    sphereData.radius,
    sphereData.widthSegments,
    sphereData.heightSegments,
    sphereData.phiStart,
    sphereData.phiLength,
    sphereData.thetaStart,
    sphereData.thetaLength
  )
  sphere.geometry.dispose()
  sphere.geometry = newGeometry
}

const icosahedronData = {
  radius: 1,
  detail: 0
}
const icosahedronFolder = gui.addFolder('Icosahedron')
icosahedronFolder.add(icosahedronData, 'radius', 0.1, 10).onChange(regenerateIcosahedronGeometry)
icosahedronFolder.add(icosahedronData, 'detail', 0, 5).step(1).onChange(regenerateIcosahedronGeometry)
icosahedronFolder.open()

function regenerateIcosahedronGeometry() {
  const newGeometry = new THREE.IcosahedronGeometry(icosahedronData.radius, icosahedronData.detail)
  icosahedron.geometry.dispose()
  icosahedron.geometry = newGeometry
}

const debug = document.getElementById('debug') as HTMLDivElement

function animate() {
    requestAnimationFrame(animate)

    renderer.render(scene, camera)

    debug.innerText = 'Matrix\n' + cube.matrix.elements.toString().replace(/,/g, '\n')

    stats.update()
}

animate()
  • 매우 긴 코드의 point 만 짚어보면 앞서 언급한 attributes position 를 수정하는 코드가 추가로 작성되었고 이를 matrix 로 수식만 변환하여 빠르게 계산하여 rendering 하는 방법과 UI 로 보는 결과는 똑같으나 사실 뒤에서 동작하는 방식은 완전히 다르다는 것만 알고가면 된다.

Buffered Geometry

Geometry 는 deprecate 되었고 그 자리를 Buffered Geometry 가 대신한다.
이 버퍼 지오메트리는 데이터를 typed arrays 로 저장하기 때문에 Mesh 를 보다 효율적으로 표현할 수 있다.
하지만 코드는 굉장히 복잡한 거 같다. 일단 기존 Geometry 와 버퍼지오메트리의 차이점을 먼저 살펴보자.

THREE.Geometry vs. THREE.BufferGeometry

특징THREE.GeometryTHREE.BufferGeometry
데이터 구조고수준 구조: 정점 배열(vertices)과 면 배열(faces)로 구성됨.저수준 구조: Float32Array로 직접 버퍼에 저장.
성능느림: JavaScript 레벨에서 정점을 처리하며 GPU로 보내기 전에 변환 필요.빠름: 데이터가 GPU 친화적인 형식으로 바로 저장됨.
유연성직관적이고 사용하기 쉬움.초기 생성은 복잡하지만 성능 및 확장성이 뛰어남.
메모리 사용비교적 비효율적: 메모리를 더 많이 소모.효율적: 메모리 사용량이 적음.
유지보수 상태더 이상 적극적으로 유지보수되지 않음.Three.js의 기본 표준으로 권장됨.
사용 예시프로토타이핑에 적합.게임, 대규모 애플리케이션, 성능 중요한 작업에 적합.

그럼 이제 코드로 보면, 예를 들어 어떤 지오메트리를 전체적으로 2만큼 욺직이겠다고 한다면 다음과 같이 코드를 작성해야한다.

기존 코드 (THREE.Geometry)

const vertices = (geometry as THREE.Geometry).vertices
for (let i = 0; i < vertices.length; i++) {
    vertices[i].multiplyScalar(2)
}
;(geometry as THREE.Geometry).verticesNeedUpdate = true

변경된 코드 (THREE.BufferGeometry)

const positions = (geometry.attributes.position as THREE.BufferAttribute).array as Array<number>
for (let i = 0; i < positions.length; i += 3) {
    const v = new THREE.Vector3(positions[i], positions[i + 1], positions[i + 2]).multiplyScalar(2)
    positions[i] = v.x
    positions[i + 1] = v.y
    positions[i + 2] = v.z
}
;(geometry.attributes.position as THREE.BufferAttribute).needsUpdate = true

사면체 생성 코드 (THREE.Geometry)

const material = new THREE.MeshNormalMaterial()
let geometry = new THREE.Geometry()
geometry.vertices.push(
    new THREE.Vector3(1, 1, 1), // a
    new THREE.Vector3(-1, -1, 1), // b
    new THREE.Vector3(-1, 1, -1), // c
    new THREE.Vector3(1, -1, -1) // d
)
geometry.faces.push(
    new THREE.Face3(2, 1, 0),
    new THREE.Face3(0, 3, 2),
    new THREE.Face3(1, 3, 0),
    new THREE.Face3(2, 3, 1)
)
geometry.computeFlatVertexNormals()
const mesh = new THREE.Mesh(geometry, material)
scene.add(mesh)

사면체 생성 코드 (THREE.BufferGeometry)

const material = new THREE.MeshNormalMaterial()
let geometry = new THREE.BufferGeometry()
const points = [
    new THREE.Vector3(-1, 1, -1), // c
    new THREE.Vector3(-1, -1, 1), // b
    new THREE.Vector3(1, 1, 1), // a

    new THREE.Vector3(1, 1, 1), // a
    new THREE.Vector3(1, -1, -1), // d
    new THREE.Vector3(-1, 1, -1), // c

    new THREE.Vector3(-1, -1, 1), // b
    new THREE.Vector3(1, -1, -1), // d
    new THREE.Vector3(1, 1, 1), // a

    new THREE.Vector3(-1, 1, -1), // c
    new THREE.Vector3(1, -1, -1), // d
    new THREE.Vector3(-1, -1, 1), // b
]
geometry.setFromPoints(points)
geometry.computeVertexNormals()

const mesh = new THREE.Mesh(geometry, material)
scene.add(mesh)

코드는 훨씬 복잡해 졌지만 WebGL 이 사용하는 GPU 친화적, 더 빠르고 메모리 효율적으로 작성되고 복잡하고 대규모 기하학 처리에 적합하기 때문에 우리는 이제 BufferGeometry 를 사용하면 된다.

profile
강정우
智(지)! 德(덕)! 體(체)!
이전 포스트

Three.js Object 3D

다음 포스트

Three.js Materials

0개의 댓글