1. 동적 계획법

⚖️ 동적계획법

• 복잡한 문제를 간단한 여러 개의 하위 문제로 나누어 푸는 방법. 이떄 하위문제의 답을 저장하여 중복 연산을 하지 않는다.

📜 example

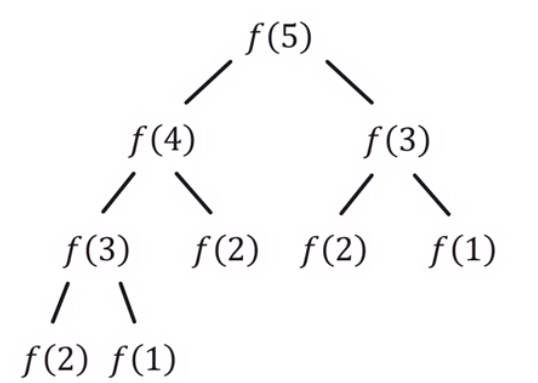
다음과 같은 문제를 풀 때

fibonacchi = {}

def fibo(n):
	if n in fibonacci:
    	return fibonacci[n]
    else:
    	fibonacci[n] = fibo(n-1) + fibo(n-2)
        return fibonacci[n]

• fibonacci 딕셔너리에 저장해둔 값을 cache(캐시)라고 하고 캐시에 저장되어있는 값을 꺼내서 쓰는 것을 memoization이라고 한다.

🛠️ 특징

• 중복되는 부분문제(overlapping subproblems)
  복잡한 문제를 나누면 작은 하위 문제들이 중복되어 나타남

• 최적 부분 구조(optimal substructure)
  현재의 최적의 해는 이전에 구했던 부분 문제의 최적해로부터 구할 수 있다.

분할정복법과 동적계획법의 차이

• 둘다 동일하게 중복되는 부분문제가 있는데 무슨 차이임?
  바로 작은 하위 문제들이 중복되어 나타나냐 마냐의 차이임

3. 시간/공간 복잡도 계산하기

⏲️ 시간 복잡도

• 간단한 재귀호출의 경우 시간의 증가가 지수로 증가한다. 하지만 동적 계획법의 경우 n번째 항을 구하기위해선 시간복잡도가 n이기 때문에 지수로 증가하는 재귀호출보다 훨씬 이점이 있다.
  

📥 공간 복잡도

• 동적 계획법은 하위 문제들의 답을 저장해놓기 때문에 하위문제의 수만큼 저장공간이 필요.

4. 동적계획법 문제풀이 테크닉

1. 점화식

복잡한 문제를 작은 하위문제로 표현한 식

점화식 정의하기

• 이 점화식을 하기위해선
  1. 구하고자하는 값이 무엇인지 정의힌다.
     f(n) : n번째 피보나치 수열
  2. 구하고자 하는 값을 부분문제들로 표현한다.
     피보나치 수열의 n번째 항은 n-1항과 n-2항의 합이다.

점화식 풀기

• 이렇게 점화식이 구해지면 2가지 방법으로 풀면된다.

  1. top-down(재귀호출 식 방법)

     1. 큰 문제를 작은 문제로 나눈다.
     2. 작은 문제를 풀어 return 해준다.

  2. bottom-up(반복문 식 방법)

     1. 작은 문제부터 차례로 풀어 적는다.
     2. 크기를 조금씩 늘려서 문제를 푼다.

2. 동적계획법 문제풀이 방법

1. 구하고자 하는 값이 무엇인지 정의하기
2. 구하고자 하는 값을 부분문제로 구성된 식으로 표현하여 점화식 구하기
3. 점화식을 재귀호출, 반복문 식으로 코드로 작성한다.