정렬 알고리즘

1) 선택 정렬

📝 정의

가장 작은 것을 선택하여 가장 앞으로 보낸다.

📋 예시)

1,5,4,7,3,6,2,10,9,8 를 오름차순으로 정렬하시오.

이때 가장 앞에서부터 순서대로 1,5,4,7,3,6,2,10,9,8 중 가장 작은 1을 index 0 번과 교환
나머지 5,4,7,3,6,2,10,9,8 중 가장 작은 2를 index 1 과 교환
나머지 4,7,3,6,5,10,9,8 중 가장 작은 3을 index 2 인 4와 위치 교환 ... 을 반복하여 sorting 을 완성한다.

그래서 가장 작은 수를 찾기 위한 task 까지 계산하면
최초 10, 9, 8 ... 하여 10+9+8... 즉, 등차 수열로 n (n + 1) / 2 의 시간 복잡도를 갖는다.
이때, n 이 무한에 가까운 굉장한 큰 값을 갖는다고 가정할 때, O 즉, Big-O 를 사용하여 +1 과 /2 는 굉장히 작은 수를 의미하기 때문에 생략하여 간단히 O(n^2) 라고 적을 수 있다.

2) 버블 정렬

📝 정의

바로 옆에 있는 값을 비교하여 더 작으면 앞으로 보낸다.

📋 예시)

1,5,4,7,3,6,2,10,9,8 를 오름차순으로 정렬하시오.

1회: 1,5,4,7,3,6,2,10,9,8
2회: 1,4,5,7,3,6,2,10,9,8
3회: 1,4,5,7,3,6,2,10,9,8
4회: 1,4,5,3,7,6,2,10,9,8
...

이런식으로 하여 10회를 해야 가장 큰 수 10의 위치를 확정할 수 있다.

즉, 1 ~ 10 까지 하면 선택 정렬과 동일하게 n (n + 1) / 2 회를 실행해야하고 이를 Big-O 표기법으로 O(N^2) 으로 표기할 수 있는데, 실제 실행을 시켜보면 시간이 버블 정렬 > 선택 정렬 이 더 크게 나온다. (버블 정렬이 더 구리다.)
why? => 위치를 바꿔주는 연산을 버블 정렬을 매 횟수 마다 실행하기 때문이다.

즉, 이론적으로 시간 복잡도는 버블 정렬 == 선택 정렬 이지만 실제로 돌려보면 위치 바꾸는 연산이 훨씬 많이 들어가기 때문에 걸리는 시간이 버블 정렬 > 선택 정렬 이렇게 된다.

3) 삽입 정렬

📝 정의

현재 index 의 숫자를 적절한 위치에 '삽입'한다.

🛠 특징

버블, 선택 정렬은 위치 변환 task 를 반드시 실행했지만 삽입 정렬은 '필요할 때만' 위치를 변환한다.

📋 예시)

1,5,4,7,3,6,2,10,9,8 를 오름차순으로 정렬하시오.

1회: 1,5,4,7,3,6,2,10,9,8
2회: 5 를 기준으로 _ 1 _ 5,4,7,3,6,2,10,9,8 => 위치 변환 X
3회: 4 를 기준으로 _ 1 _ 5 _ ,4,7,3,6,2,10,9,8 => 1 과 5 사이에 삽입
4회: 7 를 기준으로 _ 1 _ 4 _ 5 _ ,7,3,6,2,10,9,8 => 위치 변환 X
5회: 3 를 기준으로 _ 1 _ 4 _ 5 _ 7 _ ,3,6,2,10,9,8 => 1 과 4 사이에 삽입
...

이때 삽입 정렬의 특징은 현재 index 를 제외한 앞의 값들은 정렬이 되어있는 배열이라는 것이다.
즉, 모든 원소를 비교할 필요가 없고 정렬이 되어있으니 정위치를 찾기만 하면 해당 위치에 삽입을 하고 나머지 배열은 비교를 하지 않아도 된다.

말은 번지르하지만 결국 최악의 상황에는 역시 버블과 선택과 마찬가지로 10 + 9 + ... + 1 회 실행을 해야하기 때문에 Big-O 표기법으로 O(N^2) 으로 표기할 수 있다.

하지만 언급하였듯 실제로는 '필요할 때만' 위치를 변환하는 task 를 실행하기 때문에 선택, 버블 정렬보다 더 빠르다.
즉, O(N^2) 의 시간 복잡도를 갖는 개노답 정렬은 삽입 정렬 > 선택 전렬 > 버블 정렬 순으로 빠르다고 할수 있겠다.

특징으로 만약 문제가 거의 정렬된 상태라면 2,3,4,5,6,7,8,9,10,1 2~10 까지는 i 와 i+1 의비교연산만 수행하고 넘어가고 정렬 대상인 1 만 10 부터 2 까지 비교하여 적절한 위치를 찾으면 되기 때문에 이렇게 거의 정렬된 경우에서는 퀵 정렬, 힙 정렬, 병합 정렬 보다 어떤 경우엔 더 빠르거나 동일한 수준의 속도를 낼 수 있다는 특징이 있다.
그리고 연산, 메모리도 어떤 정렬보다 더 적게 먹기 때문에 가장 효율적이라 할 수 있다.

4) 퀵정렬

⏰ 시간 복잡도

O(N * logN)

🛠 특징

대표적으로 분할 정복 알고리즘을 사용하는 정렬이다.
왜 분할 정복이냐면 pivot 즉, 기준이 되는 index 를 특정하여 반으로 나누기 때문이다.

여기서 다시 고등 수학으로 돌아가 logN 이 얼마나 대단한 작은 수 냐면 예를 들어
2 ^ 20 은 1,000,000 이다.
이때 log2N(밑이 2인 로그) 에서 1,000,000 은 20 이다.
즉, 의역하자면 굉장히 방대한 데이터에서 굉장히 빠른 속도로 어떠한 연산을 수행할 수 있도록 한다는 것이다.

📋 예시)

5,4,7,3,6,1,2,10,9,8 를 정렬하시오.

1. pivot 값을 설정한다. (일반적으로 가장 앞에 있는 값을 pivot 값으로 설정한다.)
2. 그리고 그 다음 숫자인 5 부터 pivot 값 보다 더 큰 값을 특정한다.
3. 그리고 제일 마지막 숫자인 8 부터 pibot 값보다 더 작은 값을 특정한다.
4. 그리고 찾은 두 값의 위치를 바꾼다.

1회: 5,4,2,3,6,1,7,10,9,8
2회: 5,4,2,3,1,6,7,10,9,8

5. 그러면 이제 왼쪽에서 출발하는 값과 오른쪽에서 출발하는 값이 서로 엊갈리게 되는데 그럼 왼쪽에서 출발한 가장 끝 부분에 pivot 을 바꾼다. 그럼

3회: 1,4,2,3,5,6,7,10,9,8

6. 이렇게 되는데 이때, 5는 정렬이 이루어 졌다고 볼수 있다.
   그럼 이제 이를 2로 나누어 각각 다시 퀵정렬을 진행한다.

4회: 1,4,2,3, 5 ,6,7,10,9,8
5회: 1 ,4,2,3, 5,6, 7,10,9,8

...

이게 분할 정복이기 때문에 굉장히 빠른 것이다.

1 2 3 4 5 6 7 8 9 10 을 N^2 => 100 이 되는데 이를 분할하여
12345 => N^2 => 25 + 678910 => N^2 => 25 => 50 번 으로 굉장히 연산 횟수를 줄일 수 있다.

하지만 이 퀵정렬은 한가지 특징이 있는데 pivot 값을 설정하는 거에 따라서 최악의 시간복잡도는 O(N^2) 를 갖는다.
하지만 대부분의 경우엔 퀵정렬이 가장 빠르게 정렬을 수행한다.

O(N^2) 의 시간 복잡도를 경우는 아이러니 하게도 이미 정렬이 완료된 상태일 때이다.
1,2,3,4,5,6,7,8,9,10 를 정렬한다고 가정할 때,
왼쪽에서 출발하는 index 는 바로 2를 찾지만 오른쪽에서 출발하는 index 는 1인 자기 자긴까지 비교연산을 수행 후 1 의 위치를 특정한다. 이를 반복하면 결국앤 1+2+3+... 이 되어 O(N^2) 의 시간 복잡도를 갖는다.

즉, 이로서 우리는 무조건 어떤 정렬법이 더 빠르다. 라는 문장은 거짓이라는 것을 알 수 있다.
정렬이 거의 되어있는 data set 에는 삽입정렬이 가장 빠르지만 오히려 퀵정렬은 퀵 하지 못 하다는 것을 알수 있다.
따라서 상황에 맞게 본인이 필요한 알고리즘을 선택하는 것이 굉장히 중요하다.

5) 병합정렬

📝 정의

일단 반으로 쪼개고 나중에 합쳐서 정렬한다.

🛠 특징

퀵정렬과 동일하게 분할 정복 알고리즘을 사용하는 정렬이다.

퀵정렬은 pivot 값에 따라 편향되게 분할할 가능성이 있다는 점에 O(N^2)의 시간 복잡도를 갖는다. 하지만 병합정렬은 pivot 값이 존재하지 않고 정확히 반절씩 나눈다는 점에서 최악의 경우에도 O(N * logN) 의 시간 복잡도를 보장한다.

📋 예시)

5,4,7,3,6,1,2,10,9,8 를 정렬하시오.

1. 반으로 계속 쪼개어 각각의 단일 노드가 되게 한다.

5,4,7,3,6, 1,2,10,9,8

5,4,7, 3,6, 1,2,10, 9,8

...

5 4 7 3 6 1 2 10 9 8

2. 이제 2의 배수씩 합친다.

5, 4 7, 3 6, 1 2, 10 9, 8

3. 각각의 노드 내부를 정렬한다.

4, 5 3, 7 1, 6 2, 10 8, 9

4. 2번 ~ 3번을 반복한다.

4, 5, 3, 7 1, 6, 2, 10 8, 9

3, 4, 5, 7 1, 2, 6, 10 8, 9

...

정렬완료

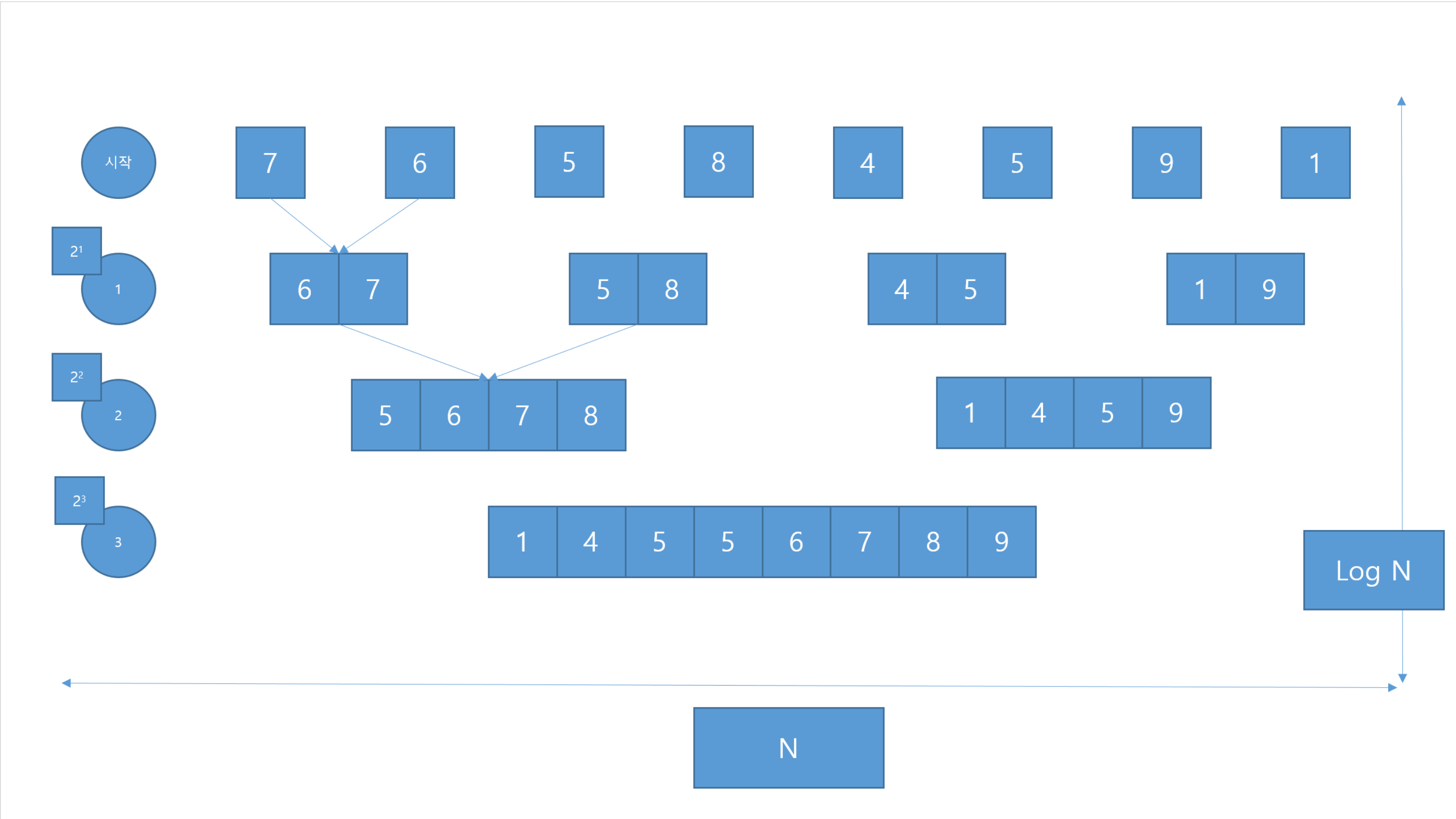
이는 너비는 N 높이는 처리하는 데이터의 개수인데 이게 2개씩 처리하기 때문에 2^1, 2^2, ... 이렇게 지수적으로 올라가기 때문에 아주 조금만 내려가도 전체 데이터를 모두 확인할 수 있다.
따라서 높이는 Log N 그러므로 가로세로 하여 `O(N logN)` 의 시간 복잡도를 갖는다.

public class MergeSort {
    public static void main(String[] args) {
        int[] q = {7, 6, 5, 8, 3, 5, 9, 1};
        mergeSort(q, 0, q.length - 1);
        System.out.println(Arrays.toString(q));
    }

    public static void merge(int[] answer, int m, int middle, int n) {
        int[] temp = new int[answer.length];
        int i = m;
        int j = middle + 1;
        int k = m;

        while (i <= middle && j <= n) {
            if (answer[i] <= answer[j]) {
                temp[k] = answer[i];
                i++;
            } else {
                temp[k] = answer[j];
                j++;
            }
            k++;
       }

        // 1. 남은 데이터는 걍 고대로 삽입
        if (middle < i) {
            for (int a = j; a <= n; a++) {
                temp[k] = answer[a];
                k++;
            }
        } else {
            for (int b = i; b <= middle; b++) {
                temp[k] = answer[b];
                k++;
            }
        }

        // 2. 나중에 정렬이 완료가 되면 본 answer 에 덮어쓴다.
        for (int t = m; t <= n; t++) {
            answer[t] = temp[t];
        }
    }

    public static void mergeSort(int[] answer, int m, int n) {
        if (m < n) {
            int middle = (m + n) / 2;
            mergeSort(answer, m, middle);
            mergeSort(answer, middle+1, n);
            merge(answer, m, middle, n);
        }
    }
}

보면 temp 변수가 매 번 배열을 선언하고 있으므로 메모리 자원의 낭비가 굉장히 크다. 이는 개선점이 될수 있고 기존의 데이터를 담을 추가적인 배열 공간이 필요하다 라는 점에서 메모리 활용이 비효율적일 수 있다. 라는 단점이 존재한다.

6) 힙 정렬

📝 정의

힙 트리 구조를 이용하는 정렬 방법이다.

힙 트리 구조란?

우선 Heap 을 알아야하고 이 Heap 을 알기 전에 Binary Tree 에 대해 알고 있어야한다.

• 이진 트리
  이 이진 트리는 데이터를 표현할 때 데이터를 각 노드에 담은 뒤에 노드를 두 개씩 이어 붙이는 구조를 말한다.

그럼 다시 Heap 에 대해 알아보자. Heap은 최솟값이나 최댓값을 빠르게 찾아내기 위해 완전 이진 트리를 기반으로하는 트리이다.
Heap 은 최대 힙과 최소 힙이 있는데 최대 힙은 부모 노드가 자식 노드보다 큰 힙이다.

그래서 일단 힙 정렬을 하기 위해서는 정해진 데이터를 힙 구조를 갖도록 만드는 것이 우선이다.
예를들어 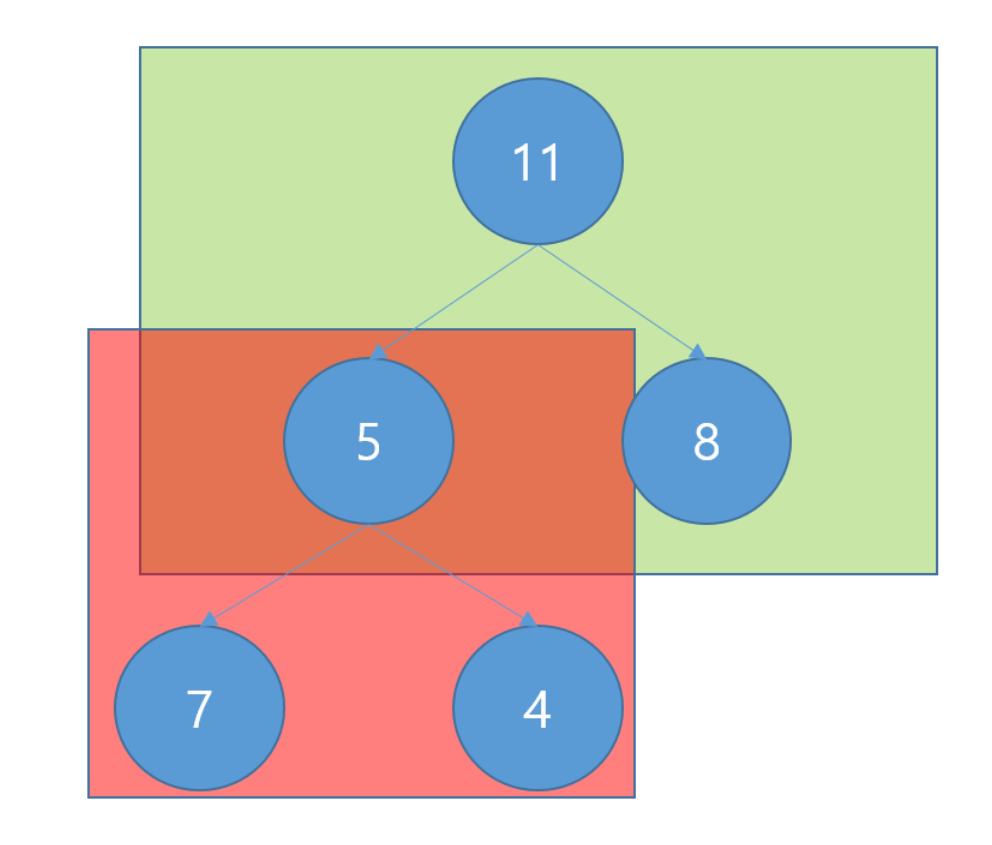초록색 네모에 포함된 3개의 노드에 대해선 Heap 정렬이 되었지만 빨간색 네모에 포함된 3개의 노드는 5 라는 단 한 개의 노드 때문에 힙이 아니게 된다. 그래서 5 의 자식 노드들 중 가장 큰 노드인 7 과 자리를 바꾸면 이제야 비로소 Heap 이진 트리가 완성되는데 이렇게 Heap 구조를 만드는 것을 힙 생성 알고리즘 (Heapify Algorithm) 이라 부른다.

그럼 이제 시간 복잡도를 구해보자. 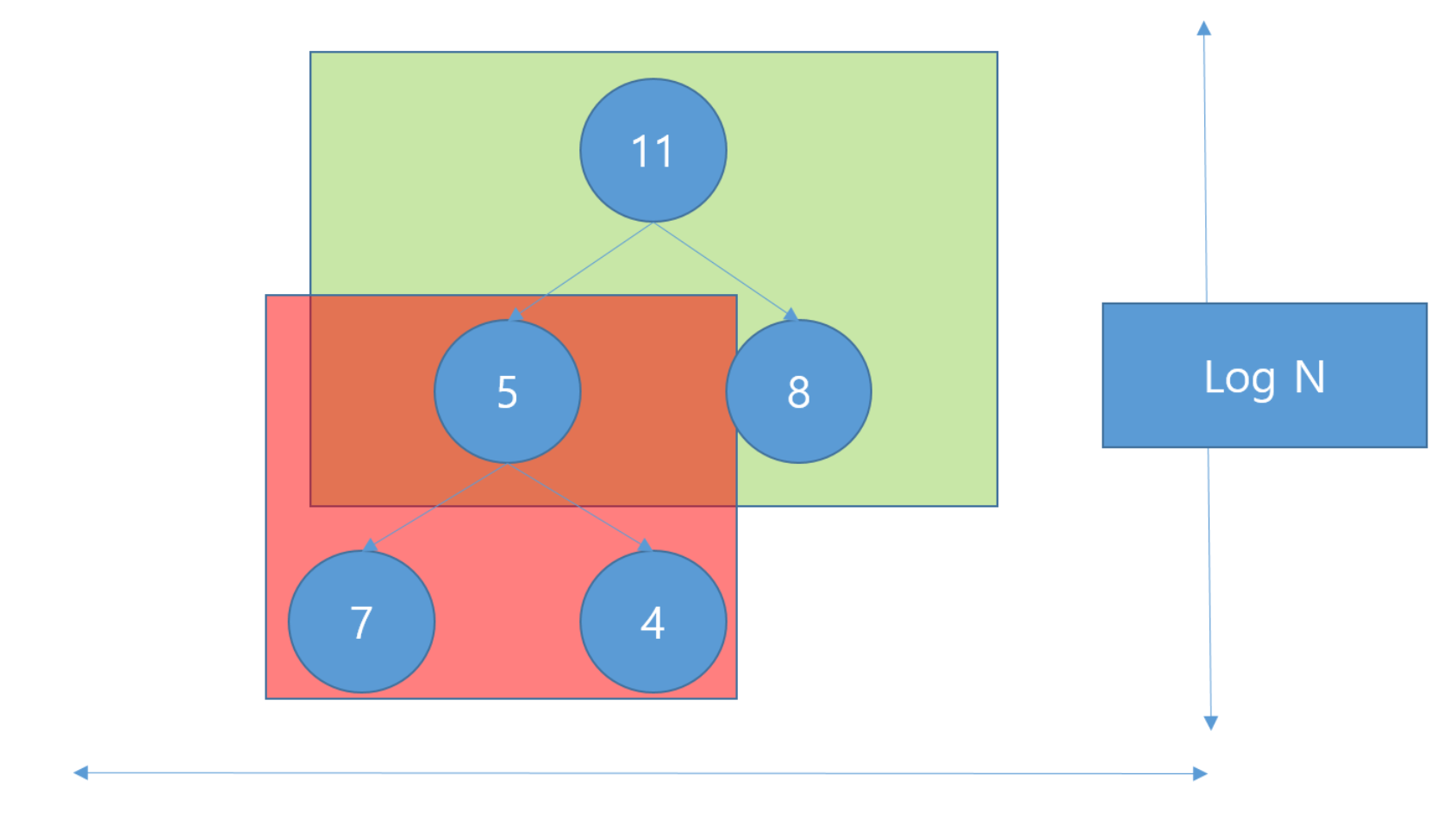다음과 같이 볼 수 있다. 높이는 이진 트리이기 때문에 n=5 일 경우 log2*5 이고 이는 반올림 하여 3이 되기 때문에 그림과 같이 3층이 되는 것이다. 따라서 높이는 Log N 으로 작성할 수 있고 여기에 모든 노드를 방문하여 heapify 를 하면 *N 이 되기 때문에 전체는 O(N * logN) 이 되는 것이다.

• 실제
  그런데 실제로 돌려보면 N/2 회수만 heapify 를 실행해주면 되는데 따라서 실제 시간 복잡도는 O(N/2 * logN) 가 되는데 여기서 N/2 > log2N 이다는 점에서 O(N) 이라고 볼 수 있다. 즉, N 번만 수행하면 전체 이진 트리를 힙 구조로 만들 수 있다는 것이다.

상향식 힙구조 vs 하향식 힙구조

상향식 힙구조 만들기 => root node 가 가장 큰 수 => 3개의 node 를 갖는 이진 트리의 대소를 비교하여 더 큰 값을 부모 node 로 옮긴다. 이를 반복한다.
오름차순 정렬하기 => 상향식 힙구조에서 가장 root node 는 가장 큰 수 이다. 따라서 가장 밑 노드와 자리를 바꾸고 해당 노를 제외 하고 heapify 를 수행한다.

하향식 힙구조 만들기 => root node 가 가장 작은 수 => 힙 구성은 배열의 마지막 절반 노드부터 시작하는 하향식 방식으로 처리하는 것이 더 효율적이다.

그럼 상향식 힙구조와 하향식 힙구조의 최종 결과물이 다른데 괜찮나? => 크게 문제는 없다. 단순히 힙구조만 만들면 나머지는 동일하게 동작하기 때문에 크게 상관은 없으나, 앞서 언급했듯 하향식이 조금 더 효율적이다.

• 힙정렬 vs 병합정렬
  힙정렬은 병합정렬보다 추가적인 메모리가 필요없기 때문에 조금 더 효율적이다라고 할 수 있다.

📋 예시)

3, 6, 4, 8, 7, 10, 2, 9, 1, 5 를 정렬하시오.

public class HeapSort {
    public static void main(String[] args) {
        StringBuilder sb = new StringBuilder();

        int[] ary = {3, 6, 4, 8, 7, 10, 2, 9, 1, 5};

        heapSort(ary);

        for (int j : ary) {
            sb.append(j).append(" ");
        }

        System.out.println(sb);
    }
    // 힙 정렬 메서드
    public static void heapSort(int[] answer) {
        int n = answer.length;

        // 최대 힙 생성
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapifyDown(answer, n, i);
        }

        // 힙 크기를 줄여가며 정렬
        for (int i = n - 1; i > 0; i--) {
            // 현재 최대값(루트)을 끝으로 이동
            swap(answer, 0, i);

            // 나머지 배열에 대해 힙 속성 재구성
            heapifyDown(answer, i, 0);
        }
    }

    // 힙 재구성 (하향식)
    private static void heapifyDown(int[] answer, int n, int root) {
        int largest = root;
        int left = 2 * root + 1;
        int right = 2 * root + 2;

        // 왼쪽 자식이 루트보다 크면 왼쪽 자식을 선택
        if (left < n && answer[left] > answer[largest]) {
            largest = left;
        }

        // 오른쪽 자식이 현재 가장 큰 값보다 크면 오른쪽 자식을 선택
        if (right < n && answer[right] > answer[largest]) {
            largest = right;
        }

        // 가장 큰 값이 루트가 아니라면 교체하고, 재귀적으로 하향식 힙 재구성
        if (largest != root) {
            swap(answer, root, largest);
            heapifyDown(answer, n, largest);
        }
    }

    // 배열 요소 교환 메서드
    private static void swap(int[] answer, int i, int j) {
        int temp = answer[i];
        answer[i] = answer[j];
        answer[j] = temp;
    }
}

7) 계수정렬

📝 정의

크기를 기준 으로만 개수를 세주면 되기 때문에 위치를 바꿀 필요 없이 모든 데이터에 한 번씩만 접근하면 된다.

🛠 특징

범위 조건이 있는 경우에 한해서 굉장히 빠른 알고리즘이다.
단, 전체 데이터의 크기만큼 배열을 생성해 줘야하기 때문에 크기가 한정되어있는 데이터에 한해서 정렬을 수행할 수 있다.

⏰ 시간 복잡도

O(N)

📋 예시)

1, 3, 2, 4, 3, 2, 5, 3, 1, 2, 3, 4, 4, 3, 5, ... 를 정렬하시오.

우선 ... 을 제외하고 위 숫자들을 정렬한다고 가정할 때,

크기 == 1	크기 == 2	크기 == 3	크기 == 4	크기 == 5
2개	3개	5개	3개	2개

이면 1을 2개 출력, 2를 3개 출력, 3을 5개 출력... 하여

1,1,2,2,2,3,3,3,3,3,4,4,4,5,5 로 출력할 수 있고 이는 겉으로 봤을 때 정렬이 된 것 처럼 보인다.

그리고 이는 위치를 바꾸는 연산이 없고 각 노드를 한 번씩 방문한다는 점에서 특정 조건에서 굉장히 빠른 알고리즘이 된다.