플로이드 와샬 알고리즘

강정우·2024년 12월 24일

algorithm

목록 보기

22/28

Floyd Warshall Algorithm

📝 정의

dijkstra 알고리즘은 한 정점에서 다른 모든 정점의 최단 경로를 구할 때 사용하여 네비게이션 같은 곳에 자주 사용된다고 하였다.
하지만 모든 정점에서 모든 정점으로의 최단 경로를 구할 땐 플로이드 와샬 알고리즘을 사용해야한다.

🛠 특징

dijkstra vs floyd warshall

다익스트라 알고리즘은 가장 적은 비용을 하나씩 선택해야 했다면,
플로이드 와샬 알고리즘은 기본적으로 거쳐가는 정점을 기준으로 알고리즘을 수행하는 점에서 그 차이점이 존재한다.

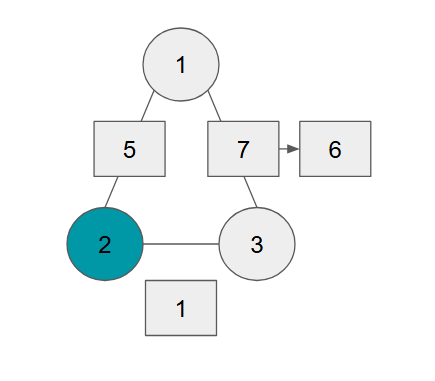다익스트라는 가장 적은 비용을 갖는 노드를 하나씩 꺼내서 해당 노드에 대해 거쳐가는 비용을 계산하여 갱신해줬다면,
플로이드 와샬은 애초에 거쳐가는 노드를 하나씩 다 설정해서 확인하는 방법이다.

⚙ 동작

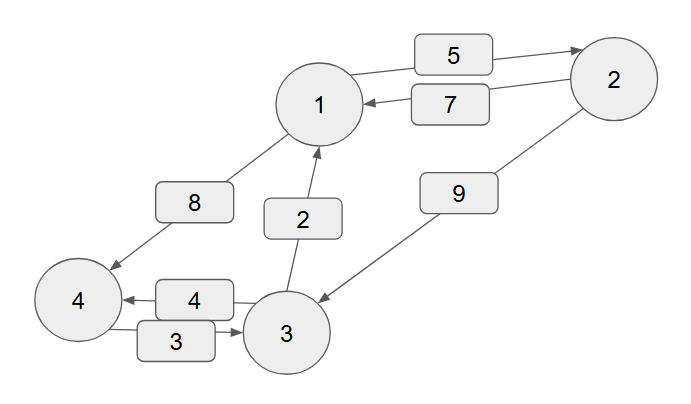위와 같은 그래프(문제)가 있다고 가정할 때

{0, 5, INF, 8},
{7, 0, 9, INF},
{2, INF, 0, 4},
{INF, INF, 3, 0},

1번 정점을 거쳐가는 경우

{0, 5, INF, 8},
{7, 0, (2->3), (2->4)},
{2, (3->2), 0, (3->4)},
{INF, (4->2), (4->3), 0},

이렇게 총 6개의 간선을 1번 정점을 거쳐가는 경우와 비교 가능하다.

예를들어 (2, 3) 을 보면 (2->3) 9 vs (2->1) 7 + (1->3) INF 이기 때문에 그냥 따로 바꾸지 않고 그냥 가는 게 더 유리하다.

그럼 하나만 더 예를들어 보자 (2, 4) 를 보면 (2->4) INF vs (2->1) 7 + (1->4) 8 따라서 INF > 15 이기 때문에 해당 값을 15로 바꿔준다

{0, 5, INF, 8},
{7, 0, 9, 15},
{2, INF, 0, 4},
{INF, INF, 3, 0},

...

{0, 5, INF, 8},
{7, 0, 9, 15},
{2, 7, 0, 4},
{INF, INF, 3, 0},

2번 정점을 거쳐가는 경우

2번 까지만 예제로 해보자. 1번 노드를 거쳐가는 경우로 계싼하여 앞서 갱신한 2차원 배열에서 이제

{0, 5, INF, 8},
{7, 0, 9, 15},
{2, 7, 0, 4},
{INF, INF, 3, 0},

{0, 5, (1->3), (1->4)},
{7, 0, 9, 15},
{(3->1), 7, 0, (3->4)},
{(4->1), INF, (4->3), 0},

(1->3) INF vs (1->2) 5 + (2->3) 9

{0, 5, 14, 8},
{7, 0, 9, 15},
{2, 7, 0, 4},
{INF, INF, 3, 0},

(1->4) 8 vs (1->2) 5 + (2->4) 15

{0, 5, 14, 8},
{7, 0, 9, 15},
{2, 7, 0, 4},
{INF, INF, 3, 0},

...

3, 4 번 노드도 동일하게 적용하여 최종적으로 다음과 같은 2차원 배열이 완성된다.

{0, 5, 11, 8},
{7, 0, 9, 13},
{2, 7, 0, 4},
{5, 10, 3, 0},

💻 코드

public class FloydWarshall {

    public static int INF = Integer.MAX_VALUE;

    public static void main(String[] args) {
        int[][] q = {
            {0, 5, INF, 8},
            {7, 0, 9, INF},
            {2, INF, 0, 4},
            {INF, INF, 3, 0}
        };
        int[][] answer = floydWarshall(q);
        for (int[] ints : answer) {
            System.out.println(" ");
            for (int anInt : ints) {
                System.out.print(anInt + " ");
            }
        }
    }

    public static int[][] floydWarshall(int[][] q) {
        // 최종 2차원 배열 생성
        int[][] distance = new int[q.length][q[0].length];

        // 정답 2차원 배열 초기화
        for(int i = 0; i < q.length; i++) {
            for(int j = 0; j < q[0].length; j++) {
                distance[i][j] = q[i][j];
            }
        }

        // 3중 for 문을 통하여 플로이드 와샬 알고리즘 구현
        for(int i = 0; i < distance.length; i++) {
            for(int j = 0; j < distance[0].length; j++) {
                for(int k = 0; k < distance.length; k++) {
                	// 다익스트라와 동일하게 overflow 를 주의하여 계산
                    if (distance[i][k] != INF && distance[k][j] != INF && distance[i][k] + distance[k][j] < distance[i][j]) {
                        distance[i][j] = distance[i][k] + distance[k][j];
                    }
                }
            }
        }

        return distance;
    }
}