Dijkstra 최단 경로 탐색 알고리즘

📝 정의

다익스트라 알고리즘은 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려준다. 다만 이때, 음의 간선을 포함할 수 없다. 물론 현실 세계에서는 음의 간선이 존재하지 않기 때문에 다익스트라는 현실 세계에 사용하기 매우 적합한한 알고리즘 중 하나이다.

🛠 특징

다이나믹 프로그래밍을 활용한 대표적인 최단경로 탐색 알고리즘이다.

다익스트라 알고리즘은 다이나믹 프로그래밍으로 분류되기도 하고 그리드 알고리즘으로 분류되기도 한다.
dp로 분류되는 이유는 최단 거리는 여러 개의 최단 거리로 이루어져 있기 때문이다.
즉, 다익스트라는 하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다.
또 그리드 알고리즘으로 분류되는 이유 중 하나는 정렬을 사용하고 정렬 후 가장 작은 값을 순서대로 사용하는 방식이 알고리즘에 포함되기 때문이다.

⚙ 동작

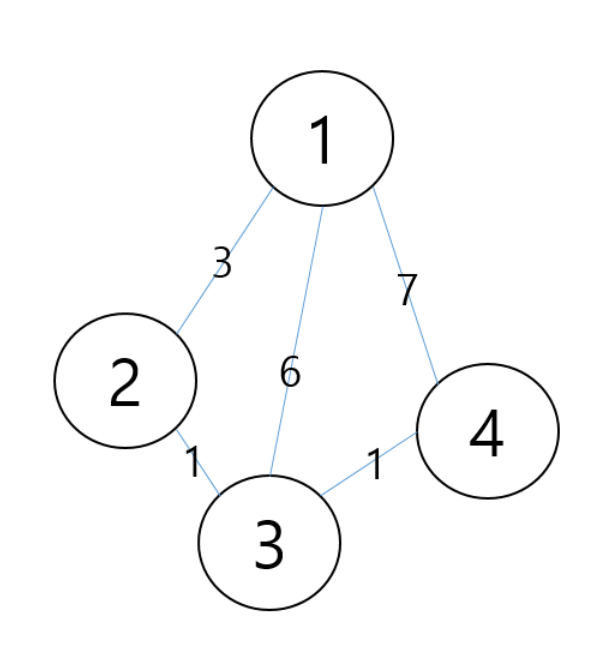1. 출발 노드 설정
최초에 1을 설정했다고 가정.

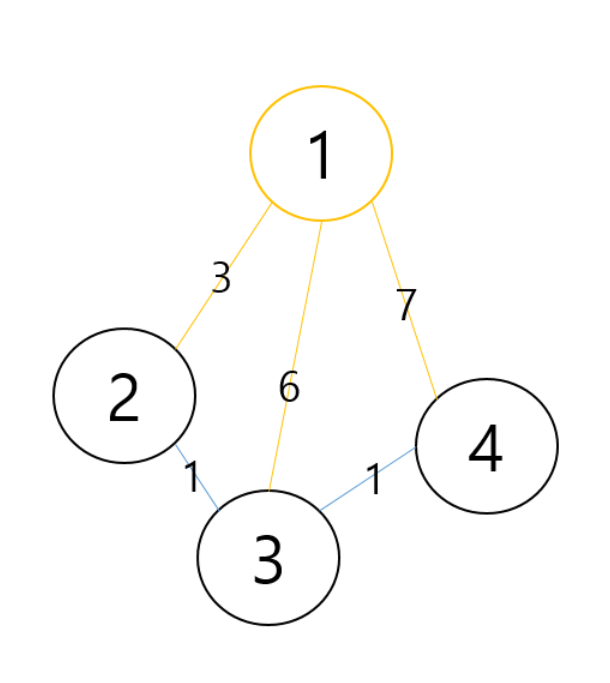2. 출발 노드를 기준으로 각 노드의 최소 비용 저장
1번 노드와 연결할 수 있는 3, 6, 7 길이의 간선들을 저장.

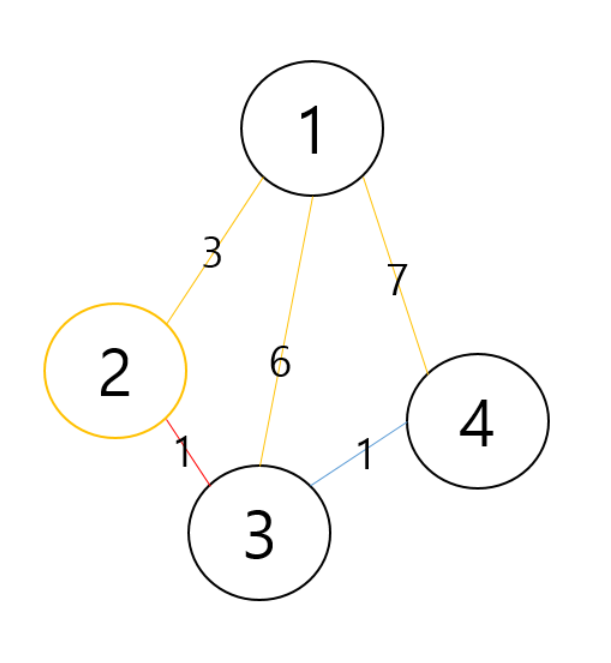3. 방문하지 않은 노드 중 가장 비용이 적은 노드를 선택
2번 노드가 방문하지 않으면서 길이 3으로 가장 비용이 적은 노드임.

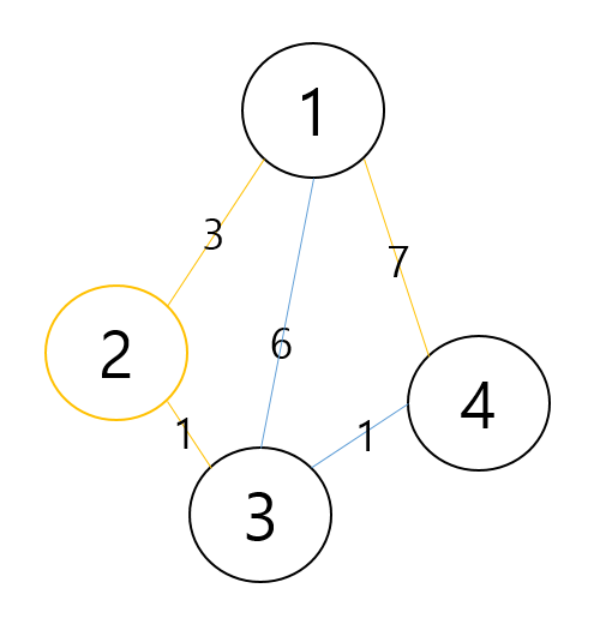4. 해당 노드를 거쳐 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신
설정한 1번 노드에서 선택한 2번을 거쳐 3번으로 가는 경우와 1번에서 바로 3번으로 가는 경우의 길이를 비교하여 최소 비용을 갱신
4 < 6 이니까 최소 비용 갱신
5. 위 과정에서 3, 4번을 반복

💻코드

• 코드로 구현할 땐, 2차원 배열을 사용한다. 최초 생성은 각 문제에 연결된 노드를 다 적고 연결되지 않은 노드는 INF 무한으로 표시해준다.

• 문제
  

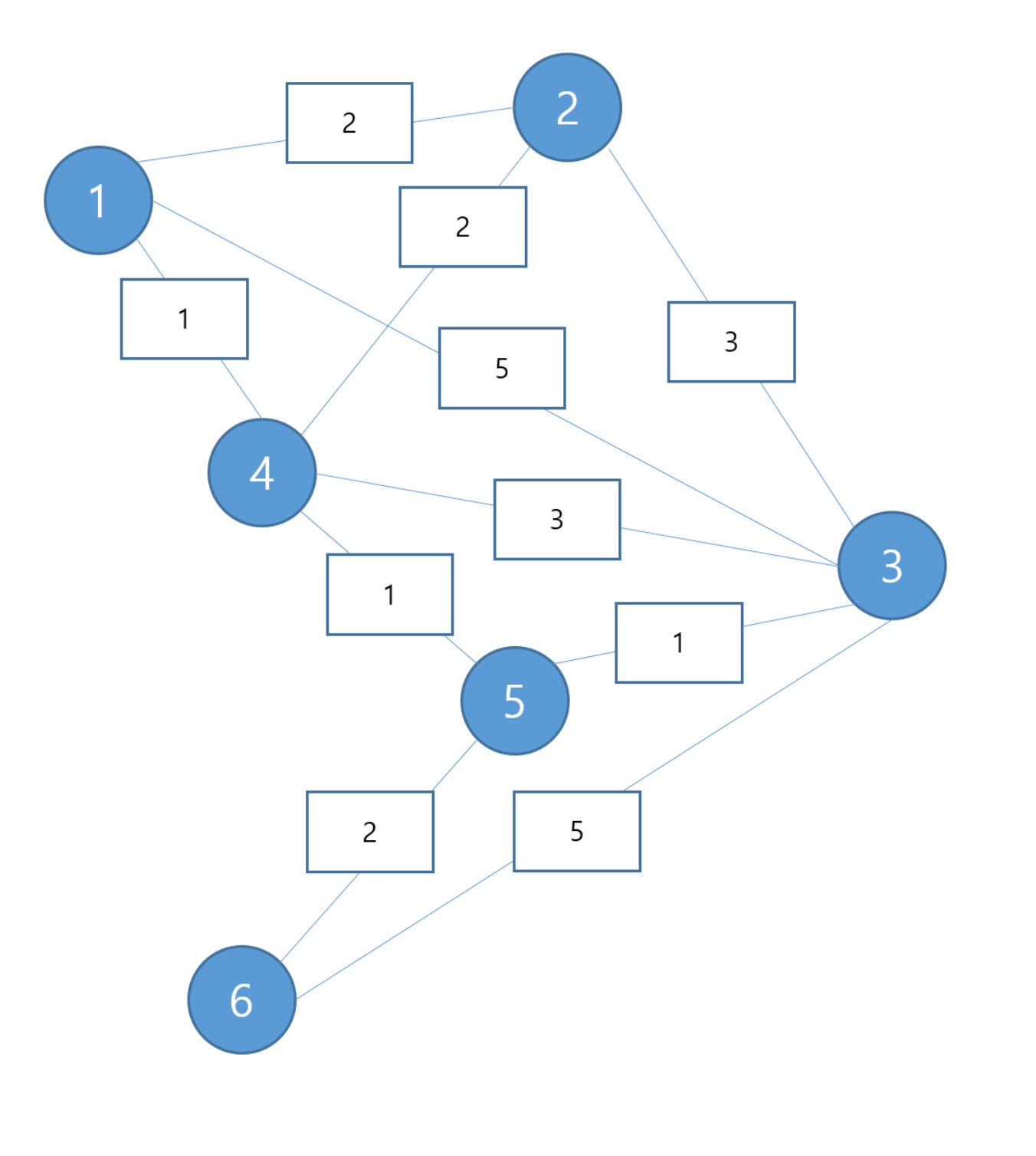
import java.util.Arrays;

public class Dijkstra {
    private static final int INF = Integer.MAX_VALUE;

    public static void main(String[] args) {
        int[][] graph = {
                {0, 2, 5, 1, INF, INF},
                {2, 0, 3, 2, INF, INF},
                {5, 3, 0, 3, 1, 5},
                {1, 2, 3, 0, 1, INF},
                {INF, INF, 1, 1, 0, 2},
                {INF, INF, 5, INF, 2, 0},
        };

        int startNode = 0;
        int[] answer = dijkstra(graph, startNode);

        for (int i : answer) {
            System.out.println("길이 = " + i);
        }
    }

    // 가장 최소 거리를 갖는 정점 반환.
    // 이는 앞에서 부터 검사하여 선형 탐색
    public static int getSmallIdx(int nodeCount, boolean[] visited, int[] distance) {
        int min = INF;
        int idx = 0;

        for (int i = 0; i < nodeCount; i++) {
            if (!visited[i] && (distance[i] < min)) {
                min = distance[i];
                idx = i;
            }
        }

        return idx;
    }

    public static int[] dijkstra(int[][] graph, int startNode) {
        int nodeCount = graph.length;
        boolean[] visited = new boolean[nodeCount];
        int[] distance = new int[nodeCount];
        System.arraycopy(graph[startNode], 0, distance, 0, nodeCount);
        visited[startNode] = true;
        // 시간 복잡도가 O(N^2) 으로 아주 느림.
        for (int i = 0; i < nodeCount - 2; i++) {
            int current = getSmallIdx(nodeCount, visited, distance);
            visited[current] = true;
            for (int j = 0; j < nodeCount; j++) {
                // 방문하지 않은 노드 && 오버플로우가 나지 않도록 하는 조건 && 다음 노드에 비해 더 작은 값을 갖는 경우
                if (!visited[j] && distance[current] != INF && graph[current][j] != INF && distance[current] + graph[current][j] < distance[j]) {
                    distance[j] = distance[current] + graph[current][j];
                }
            }
        }

        return distance;
    }
}

여기서 우리는 해당 노드와 연결된 모든 노드와 비교 작업은 반드시 필요하여 N 번 만큼 수행해야 하지만, getSmallIdx 와 같은 최솟값을 찾아오는 함수는 Heapify 가 된 트리라면 최솟값을 찾는데 logN 번 수행하기 때문에 O(N^2) => O(NlogN) 까지 줄일 수 있다.

💻코드 O( NlogN ) ver

import java.util.Arrays;
import java.util.PriorityQueue;

public class Dijkstra {
    private static final int INF = Integer.MAX_VALUE;

    public static void main(String[] args) {
        int[][] graph = {
                {0, 2, 5, 1, INF, INF},
                {2, 0, 3, 2, INF, INF},
                {5, 3, 0, 3, 1, 5},
                {1, 2, 3, 0, 1, INF},
                {INF, INF, 1, 1, 0, 2},
                {INF, INF, 5, INF, 2, 0},
        };

        int startNode = 0;
        int[] answer = dijkstra(graph, startNode);

        for (int i = 0; i < answer.length; i++) {
            System.out.println("Node " + i + " : " + answer[i]);
        }
    }

    public static int[] dijkstra(int[][] graph, int startNode) {
        int nodeCount = graph.length;
        int[] distance = new int[nodeCount];
        boolean[] visited = new boolean[nodeCount];

        // 거리 초기화
        Arrays.fill(distance, INF);
        distance[startNode] = 0;

        // 우선순위 큐: (거리, 노드 번호)
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(a[0], b[0]));
        pq.offer(new int[]{0, startNode});

        while (!pq.isEmpty()) {
            int[] current = pq.poll();
            int currentDistance = current[0];
            int currentNode = current[1];

            // 이미 방문한 노드이면 무시
            if (visited[currentNode]) continue;
            visited[currentNode] = true;

            // 인접 노드 거리 갱신
            for (int i = 0; i < nodeCount; i++) {
                if (graph[currentNode][i] != INF && !visited[i]) {
                    int newDistance = currentDistance + graph[currentNode][i];
                    if (newDistance < distance[i]) {
                        distance[i] = newDistance;
                        pq.offer(new int[]{newDistance, i});
                    }
                }
            }
        }

        return distance;
    }
}