🌼 15787. 기차가 어둠을 헤치고 은하수를
문제
N개의 기차가 어둠을 헤치고 은하수를 건너려고 한다.
기차는 20개의 일렬로 된 좌석이 있고, 한 개의 좌석에는 한 명의 사람이 탈 수 있다.
기차의 번호를 1번부터 N번으로 매길 때, 어떠한 기차에 대하여 M개의 명령이 주어진다.
명령의 종류는 4가지로 다음과 같다.
1 i x : i번째 기차에(1 ≤ i ≤ N) x번째 좌석에(1 ≤ x ≤ 20) 사람을 태워라. 이미 사람이 타있다면 , 아무런 행동을 하지 않는다.
2 i x : i번째 기차에 x번째 좌석에 앉은 사람은 하차한다. 만약 아무도 그자리에 앉아있지 않았다면, 아무런 행동을 하지 않는다.
3 i : i번째 기차에 앉아있는 승객들이 모두 한칸씩 뒤로간다. k번째 앉은 사람은 k+1번째로 이동하여 앉는다. 만약 20번째 자리에 사람이 앉아있었다면 그 사람은 이 명령 후에 하차한다.
4 i : i번째 기차에 앉아있는 승객들이 모두 한칸씩 앞으로간다. k번째 앉은 사람은 k-1 번째 자리로 이동하여 앉는다. 만약 1번째 자리에 사람이 앉아있었다면 그 사람은 이 명령 후에 하차한다.
M번의 명령 후에 1번째 기차부터 순서대로 한 기차씩 은하수를 건너는데 조건이 있다.
기차는 순서대로 지나가며 기차가 지나갈 때 승객이 앉은 상태를 목록에 기록하며 이미 목록에 존재하는 기록이라면 해당 기차는 은하수를 건널 수 없다.
예를 들면, 다음 그림을 예로 들었을 때, 1번째 기차와 같이 승객이 앉은 상태는 기록되지 않았기 때문에 은하수를 건널 수있다. 2번째 기차와 같은 상태도 기록되지 않았기 때문에 2번째 기차도 은하수를 건널 수 있다. 3번째 기차는 1번째 기차와 승객이 앉은 상태가 같으므로 은하수를 건널 수 없다.

처음에 주어지는 기차에는 아무도 사람이 타지 않는다.
은하수를 건널 수 있는 기차의 수를 출력하시오.
입력
입력의 첫째 줄에 기차의 수 N(1 ≤ N ≤ 100000)과 명령의 수 M(1 ≤ M ≤ 100000)가 주어진다. 이후 두 번째 줄부터 M+1번째 줄까지 각 줄에 명령이 주어진다.
출력
은하수를 건널 수 있는 기차의 수를 출력하시오.
예제 입력 1
5 5
1 1 1
1 1 2
1 2 2
1 2 3
3 1
예제 출력 1
2
알고리즘 분류
- 구현
- 비트마스킹
코드 - python3 성공
from collections import deque
import sys
input = sys.stdin.readline
n, m = map(int, input().split()) # n: 기차 수, m: 명령 수
order = list(tuple(map(int, input().split())) for _ in range(m)) # m개의 명령 입력
train = [deque(0 for _ in range(20)) for _ in range(n)] # n개의 기차 좌석 선언
for i in range(m): # 명령 개수 만큼 탐색
if order[i][0] == 1: # 1 i x
train[order[i][1]-1][order[i][2]-1] = 1 # 탑승
elif order[i][0] == 2: # 2 i x
train[order[i][1]-1][order[i][2]-1] = 0 # 하차
elif order[i][0] == 3: # 3 i
train[order[i][1]-1].rotate(1) # 전체 +1
train[order[i][1]-1][0] = 0 # 맨앞 비우기
else: # 4 i
train[order[i][1]-1].rotate(-1) # 전체 -1
train[order[i][1]-1][-1] = 0 # 맨뒤 비우기
output_train = [] # 은하수를 건널 수 있는 기차
for i in range(n): # 기차 수 만큼 탐색
if train[i] not in output_train: # 중복되지 않는다면 저장
output_train.append(train[i])
print(len(output_train))🌼 15500. 이상한 하노이 탑
문제
승민이는 기존 하노이 탑 문제를 약간 변형한 이상한 하노이 탑 문제를 만들었다.
이상한 하노이 탑 문제와 기존 하노이 탑 문제와 다른 점이 2가지가 있는데 하나는 "쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.(중간 과정 역시 그래야함)" 라는 조건이 삭제되었다는 점이고 또 다른 하나는 첫 번째 장대에 원판들이 반경 상관없이 무작위로 배치되어 있다는 점이다.
승민이는 이 문제를 진수에게 주었고 원판을 옮긴 횟수가 12345보다 같거나 작으면 피자를 사주기로 하였다. 진수를 도와 피자를 먹게 해주자!
입력
첫 번째 줄에는 원판의 개수 N (1 ≤ N ≤ 123) 이 주어진다.
두 번째 줄에는 첫 번째 장대에 있는 원판들의 반경 나타내는 정수 ai (1 ≤ ai ≤ N) 들이 공백을 두고 주어진다. (제일 아래에 있는 원판의 반경부터 주어진다.)
출력
첫 번째 줄에 원판을 옮긴 횟수 K (0 ≤ K ≤ 12345) 를 출력한다.
다음 K 개 줄에 걸쳐 A B (1 ≤ A, B ≤ 3) 를 출력하는데 A 번째 장대 맨위에 있는 원판 하나를 B 번째 장대 맨위로 옮긴다는 뜻이다.
예제 입력 1
3
2 3 1
예제 출력 1
4
1 2
1 3
1 3
2 3
힌트
아래는 예제를 푸는 과정을 나타낸다.
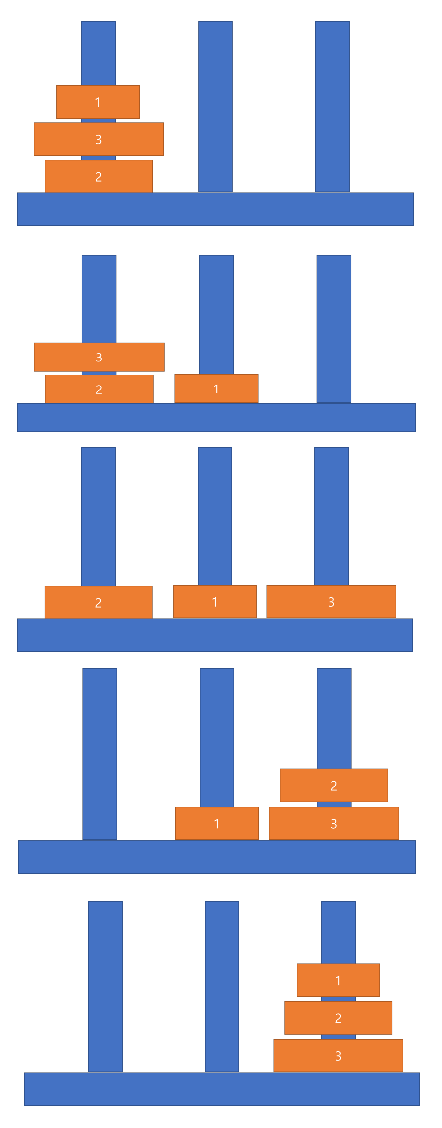
알고리즘 분류
- 구현
- 자료 구조
- 시뮬레이션
- 스택
코드 - python3 성공
import sys
input = sys.stdin.readline
N = int(input()) # 원판 갯수
targetNum = N # 목표 숫자
cnt = 0 # 옮긴횟수
result = [] # 옮긴루트
First = [] # 첫번째 장대
Second = [] # 두번째 장대
numbers = list(map(int, input().split())) # 원판 반경 정보
for num in numbers:
First.append(num)
while targetNum > 0: # 타겟 숫자가 0이 될 때까지 반복
if targetNum in First: # First 장대 스택에 targetNum이 있을 때
while First:
now = First.pop() # 스택의 가장 위에 있는 숫자를 꺼내서 now에 저장
if now == targetNum:
result.append("1 3") # 첫 번째 스택에서 세 번째 스택으로 이동
cnt += 1 # 옮긴횟수
targetNum -= 1
break
else:
result.append("1 2") # 첫 번째 스택에서 두 번째 스택으로 이동
cnt += 1
Second.append(now)
elif targetNum in Second:
while Second:
now = Second.pop() # Second 장대 스택의 가장 위에 있는 숫자를 꺼내서 now에 저장
if now == targetNum:
result.append("2 3") # 두 번째 스택에서 세 번째 스택으로 이동
cnt += 1
targetNum -= 1
break
else:
result.append("2 1") # 두 번째 스택에서 첫 번째 스택으로 이동
cnt += 1
First.append(now)
print(cnt)
print("\n".join(result))
🌼 14284. 간선 이어가기 2
문제
정점 n개, 0개의 간선으로 이루어진 무방향 그래프가 주어진다. 그리고 m개의 가중치 간선의 정보가 있는 간선리스트가 주어진다. 간선리스트에 있는 간선 하나씩 그래프에 추가해 나갈 것이다. 이때, 특정 정점 s와 t가 연결이 되는 시점에서 간선 추가를 멈출 것이다. 연결이란 두 정점이 간선을 통해 방문 가능한 것을 말한다.
s와 t가 연결이 되는 시점의 간선의 가중치의 합이 최소가 되게 추가하는 간선의 순서를 조정할 때, 그 최솟값을 구하시오.
입력
첫째 줄에 정점의 개수 n, 간선리스트의 간선 수 m이 주어진다.(2≤n≤5000,1≤m≤100,000)
다음 m줄에는 a,b,c가 주어지는데, 이는 a와 b는 c의 가중치를 가짐을 말한다. (1≤a,b≤n,1≤c≤100,a≠b)
다음 줄에는 두 정점 s,t가 주어진다. (1≤s,t≤n,s≠t)
모든 간선을 연결하면 그래프는 연결 그래프가 됨이 보장된다.
출력
s와 t가 연결되는 시점의 간선의 가중치 합의 최솟값을 출력하시오,
예제 입력 1
8 9
1 2 3
1 3 2
1 4 4
2 5 2
3 6 1
4 7 3
5 8 6
6 8 2
7 8 7
1 8
예제 출력 1
5
알고리즘 분류
- 그래프 이론
- 데이크스트라
- 최단 경로
코드
import heapq
import sys
INF = sys.maxsize # 무한대
input = sys.stdin.readline
# 다익스트라 알고리즘
def dijkstra(start):
q = []
heapq.heappush(q, (0, start)) # 시작 노드 큐에 추가, 거리 0
dis[start] = 0 # 시작 노드 거리 0 초기화
while q: # 큐가 빌때까지 반복
d, now = heapq.heappop(q) # 거리 d와 현재 노드 now를 꺼냄
if dis[now] < d: # 현재 노드까지의 거리가 이미 더 짧다면 스킵
continue
for v, w in graph[now]: # 현재 노드에서 갈 수 있는 모든 인접 노드에 대해
cost = d + w # 시작 노드에서 현재 노드까지의 거리 d에 해당 간선의 가중치 w를 더하여 다음 노드까지의 거리 cost를 계산
if cost < dis[v]: # 거리 cost가 기존의 거리 dis[v]보다 짧으면
dis[v] = cost # 다음 노드까지의 거리를 업데이트
heapq.heappush(q, (cost, v)) # 큐에 다음 노드와 새로운 거리 cost를 추가
n, m = map(int, input().split()) # 정점 개수, 간선리스트의 간선 수
graph = [[] for _ in range(n+1)] # a, b, c
dis = [INF]*(n+1) # 거리 무한대로 초기화
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append((b, c)) # 노드 a에서 b로 가는 간선 가중치 c를 그래프에 추가
graph[b].append((a, c)) # 노드 b에서 a로 가는 간선 가중치 c도 그래프에 추가
s, t = map(int, input().split()) # 시작 노드 s와 목표 노드 t
dijkstra(s)
print(dis[t])