🍃 boj 6615. 콜라츠 추측
문제
콜라츠 추측은 흥미로운 현상이다. 이 법칙은 간단해보이지만, 수학적으로 아직까지 증명되어있지 않은 문제이다. 우리는 이 추측이 옳다고 받아들이겠다.
콜라츠 추측을 설명하면 다음과 같다. 우선 다음과 같은 양의 정수 수열 xi 를 생각하자.
만약 xi 가 짝수이면, xi+1=xi/2
만약 xi 가 홀수이면, xi+1=3*xi +1 이다.
콜라츠 추측은 이렇게 만든 수열은 결국 1이 된다는 것이다.
과학자들은, 컴퓨터를 이용하여 첫 번째 수열이 258 보다 작으면, 이 추측은 참이라고 증명했다.
이제 문제를 보자.
두개의 양의 정수를 준다. 각각의 수에 대해서 콜라츠 추측으로 만든 수열을 생각하자.
각각의 수열을 비교하였을때 처음으로 같은 숫자가 나왔을때 , 각각 몇번째 수열에서 만나는지 구해본다. 문제의 편의를 위해, 이 수열은 1이 나오면 더이상 진행하지 않는다고 하자. ( 1 다음에 나올 수열을 생각하면, 1, 4, 2, 1, 4, 2, 1로 반복되기 때문이다.)
입력
입력은 몇개의 테스트 케이스로 구성된다. 각 테스트 케이스는 두개의 정수 A와 B가 주어진다. ( 1 ≤ A, B ≤ 1,000,000) 마지막 줄은 두개의 0으로 구성된다.
출력
각각의 테스트 케이스마다 다음과 같은 문장을 한줄에 출력한다.
"A needs SA steps, B needs SB steps, they meet at C"
SA와 SB는 A와 B로 수열을 만들고, 처음으로 같은 숫자 C가 나왔을때 각각의 수열에서 몇번째 인지 알려주는 숫자이다.
예제 입력 1
7 8
27 30
0 0
예제 출력 1
7 needs 13 steps, 8 needs 0 steps, they meet at 8
27 needs 95 steps, 30 needs 2 steps, they meet at 46
알고리즘 분류
- 브루트포스 알고리즘
- 트리
- 최소 공통 조상
코드 - python3 성공
# xi+1 = xi / 2
# xi+1 = 3*xi + 1
# 예제1 로직 과정
# 7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
# 8 4 2 1
import sys
input = sys.stdin.readline
while True:
A, B = map(int,input().split()) # 두 양의 정수
# 종료 조건
if A == 0 and B == 0: break
# 정수 A에 대한 비교
temp = A
a = [-1, A] # 첫 번재 수에 대한 수열
while True:
# 종료 조건
if temp == 1: break
# 홀수일 때
if temp % 2:
temp = 3 * temp + 1
a.append(temp)
# 짝수일 때
else:
temp //= 2
a.append(temp)
# 정수 B에 대한 비교
temp = B
b = [-2, B] # 두 번째 수에 대한 수열
while True:
# 종료 조건
if temp == 1: break
# 홀수일 때
if temp % 2:
temp = 3 * temp + 1
b.append(temp)
# 짝수일 때
else:
temp //= 2
b.append(temp)
# 리스트 거꾸로 순환
for i in range(-1, -1000000000, -1):
if a[i] != b[i]:
break
print(f'{A} needs {len(a) + i} steps, {B} needs {len(b) + i} steps, they meet at {a[i + 1]}')🍃 boj 9239. 스티브 잡숭
문제
스티브 잡숭은 남들 앞에서 발표할 때, 수학 트릭을 이용해 청중의 관심을 끌어모은다.
첫 번째로 어떤 수의 제곱근이 그 수의 절반 뒷 부분이라는 트릭 (
(\sqrt{25}=5),
(\sqrt{5776} = 76))을 말하고, 그 다음에는 어떤 수에 X = 2.6을 곱하면, 그 수의 첫 자리를 맨 뒷자리로 보낸 수가 된다는 트릭을 말한다. (
(135 \times 2.6 = 351),
(270270 \times 2.6 = 702702))
사람들은 두 번째 트릭에 열광했고, 잡숭은 X = 2.6을 제외한 다른 숫자를 찾으려고 한다.
X가 주어졌을 때, X를 곱했을 때, 결과가 원래 숫자의 첫 자리를 맨 뒷자리로 보낸 수가 되는 모든 숫자를 찾는 프로그램을 작성하시오.
입력
첫째 줄에 X (1 ≤ X < 1000)가 주어진다. X는 최대 소수점 4째 자리까지 주어진다.
출력
108보다 작은 모든 자연수 중에 X를 곱했을 때 결과가 원래 숫자의 첫 번째 자리를 맨 뒷자리로 보낸 수가 되는 모든 숫자를 한 줄에 하나씩 증가하는 순서대로 출력한다.
만약, 그러한 수가 없는 경우에는 No solution을 출력한다.
예제 입력 1
2.6
예제 출력 1
135
270
135135
270270
예제 입력 2
3.1416
예제 출력 2
No solution
알고리즘 분류
- 수학
- 브루트포스 알고리즘
코드 - 시간초과
import sys
input = sys.stdin.readline
# 2.6이 아닌 다른 수를 곱했을 때 맨 앞 수가 맨 뒤로 가게 해보자. -> 모든 수 구하기
X = float(input())
answer = []
for i in range(100000000):
first = i // 10**(len(str(i))-1) # 맨 앞자리 수
rest = i % 10**(len(str(i))-1) # 나머지 수
if (X * i == rest*10 + first):
answer.append(i)
if len(answer) == 0:
print("No solution")
else: print(*answer)🍃 4563. 리벤지 오브 피타고라스
문제
피타고라스의 정리는 직각삼각형의 세 변의 관계를 나타내는 정리이다. 빗변의 길이를 C, 다른 두 변의 길이를 A, B라고 한다면 다음과 같은 식으로 쓸 수 있다.
A2 + B2 = C2
세 변의 길이가 모두 자연수인 직각삼각형 중에 가장 유명한 삼각형은 아래와 같다.
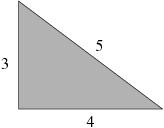
A = 12인 경우에는 다음과 같이 두 개의 직사각형을 찾을 수 있다.
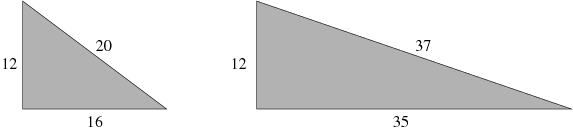
A가 주어졌을 때, 빗변의 길이 C가 자연수인 직각삼각형을 만드는 자연수 B (B > A)는 몇 개가 있을까?
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 자연수 A (2 ≤ A < 220)이 주어진다. 입력의 마지막 줄에는 0이 하나 주어진다.
출력
입력으로 주어진 A에 대해서, 빗변의 길이가 자연수인 직각삼각형을 만드는 B(B>A)의 개수를 출력한다.
예제 입력 1
3
12
2
1048574
1048575
0
예제 출력 1
1
2
0
1
175
알고리즘 분류
- 수학
- 기하학
- 정수론
- 피타고라스 정리
코드 - python3 성공
import sys
input = sys.stdin.readline
while True:
A = int(input())
if A == 0:
break
A2 = A**2
# 삼각형이 될 조건
# c < a + b
# a^2 = c^2 - b^2
# a^2 = (c - b)(c + b)
cnt = 0
for i in range(1, A + 1):
if A2 % i == 0: # A의 약수인 i 구하기
B = i
C = A2 // i
if (C - B) // 2 > A and (B + C) % 2 == 0: # 삼각형이 될 조건: 삼각형 한변의 길이, 삼각형 둘레가 짝수인가
cnt += 1
print(cnt)
🍃 9252. LCS 2
문제
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
입력
첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.
출력
첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를, 둘째 줄에 LCS를 출력한다.
LCS가 여러 가지인 경우에는 아무거나 출력하고, LCS의 길이가 0인 경우에는 둘째 줄을 출력하지 않는다.
예제 입력 1
ACAYKP
CAPCAK
예제 출력 1
4
ACAK
알고리즘 분류
다이나믹 프로그래밍
코드 - python3 런타임 에러 / pypy 런타임 에러
import sys
input = sys.stdin.readline
N = 1001
s = [[0] * N for _ in range(N)] # DP테이블 초기화
a = input()
b = input()
def print_lcs(i, j): # LCS 출력 재귀 함수
if s[i][j] == 0: # LCS 길이가 0이라면 함수 종료
return
if a[i - 1] == b[j - 1]: # 현재 위치에서 문자가 일치하는 경우
print_lcs(i - 1, j - 1) # 현재 위치의 문자를 출력
print(a[i - 1], end="") # 대각선 위치로 이동하여 재귀 호출
else: # 현재 위치에서 문자가 일치하지 않는 경우
print_lcs(i - 1, j) if s[i - 1][j] > s[i][j - 1] else print_lcs(i, j - 1) # 조건 만족시 위쪾으로 이동, 그렇지 않으면 왼쪽으로 이동
i = 0
j = 0
for i in range(len(a)): # a 문자열 탐색
for j in range(len(b)): # b 문자열 탐색
if a[i] == b[j]: # 두 문자가 일치하는 경우
s[i + 1][j + 1] = s[i][j] + 1 # 이전 대각선 값 + 1
else: # 일치하지 않는 경우
s[i + 1][j + 1] = max(s[i][j + 1], s[i + 1][j]) # 이전 행과 열 중에서 더 큰 값
print(s[i][j])
print_lcs(i, j)