26646. 알프스 케이블카

문제

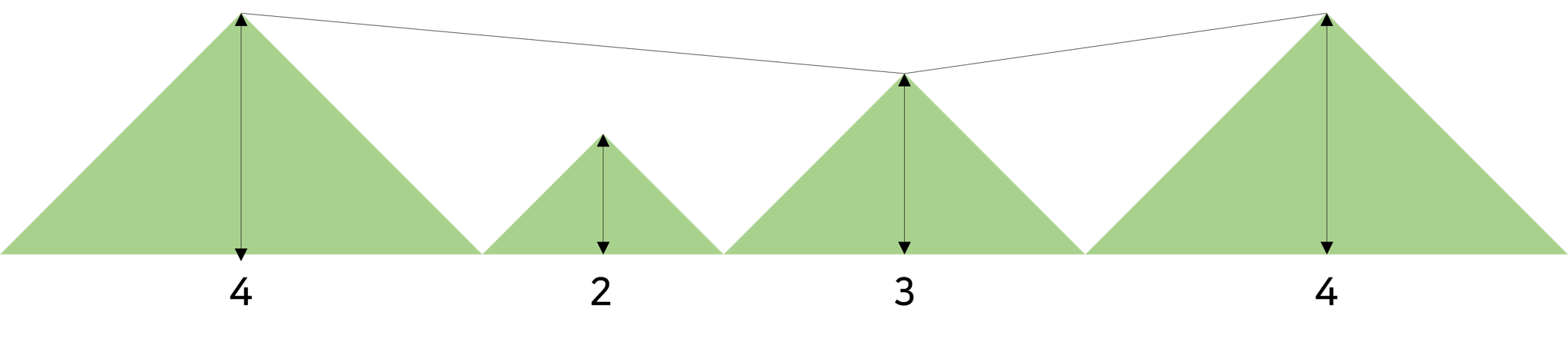
ALPS 부원들은 친목 도모를 위해 다 같이 알프스 산맥으로 여행을 떠났다! 알프스 산맥은
$N$개의 산이 겹치거나 빈 부분 없이 일렬로 나열된 형태이며, 왼쪽에서부터
$i$번째에 위치한 산은 빗변을 아래로 하며 높이가
$H_i$인 직각 이등변 삼각형이다.

ALPS 부원들은 체력이 좋지 않기 때문에
$1$번 산에서 시작해
$N$번 산에서 끝나는 케이블카 노선을 설치해 산을 오르려 한다. 노선을 설치하는 법은 다음과 같다.

1.  $1$번 산의 정상과 다른 산의 정상을 직선으로 잇는 와이어를 설치하고, 다시 그 산의 정상에서 다른 산의 정상으로 와이어를 설치한다. 이 때 와이어는 산을 가로질러 설치될 수 있다.
2. 이를 $N$번 산을 끝으로 할 때까지 자유롭게 반복한다.
   각 와이어의 설치 비용은 설치해야 할 와이어 길이의 제곱과 같으며 노선의 설치 비용은 사용한 와이어의 설치 비용의 합이다. ALPS 부원들을 위해
   $1$번 산에서 시작해
   $N$번 산에서 끝나는 노선을 설치하기 위한 최소 비용을 구해보자.

입력

첫 번째 줄에 알프스 산맥을 이루는 산의 수
$N$이 주어진다.
$(2 \leq N \leq 50\,000)$ 

두 번째 줄에 각 산의 높이
$H_1, H_2, \cdots, H_N$이 공백으로 구분되어 정수로 주어진다.
$(1 \leq H_i \leq 100)$ 

출력

$1$번 산에서 시작해
$N$번 산에서 끝나는 노선을 설치하기 위한 최소 비용을 출력한다.

예제 입력 1

4
4 2 3 4

예제 출력 1

116

예제 입력 2

2
1 1

예제 출력 2

4

알고리즘 분류

• 수학
• 그리디 알고리즘
• 기하학
• 애드 혹

코드

import sys
input = sys.stdin.readline

n = int(input())
arr = list(map(int, input().split()))
answer = 0

# c**2 = a**2 + b**2
# 피타고라스 공식 사용
for i in range(n-1):
    answer += (arr[i] + arr[i+1])**2 + (arr[i] - arr[i+1])**2
print(answer)

---

13270. 피보나치 치킨

문제

KAIST 주변에서 먹을 수 있는 배달 음식들은 대부분 치킨이다. 이렇게 치킨집이 포화 상태지만 지훈이는 카이스트 주변에 새로 치킨집을 창업했는데, 생각보다 장사가 잘 되었다!

알고 보니 그가 차린 치킨집의 신기한 방식 때문에 장사가 잘 된다고 한다. 지훈이의 치킨집에 치킨 주문을 하는 것은 간단하다. 어차피 지훈이네 치킨집의 메뉴는 도깨비오븐구이 하나이므로, 치킨 먹을 사람 수만 이야기하면, 그 사람 수에 맞는 치킨을 배달하는 것이다.

치킨의 마리 수를 정하는 방법은 다음과 같다:

1. 2인 1닭, 3인 2닭, 5인 3닭, 8인 5닭, 13인 8닭 … 등 피보나치 수열의 인접한 두 수를 이용해(항상 사람의 수 > 닭의 수가 되어 야 한다) 치킨 세트를 만든다.

2. 이 세트들을 적절히 조합해서 총 합이 정확히 N인분이 되도록 만든다.

3. 2번 과정에서 조합한 세트들을 배달한다.
   어느 날, 지훈이의 치킨집 단골인 태영이가 N명이 먹을 것을 주문하면 배달되는 치킨 수의 범위가 궁금해졌다. 똑같이 N인분을 주문한다고 해서 항상 같은 마리수의 닭이 오는 것은 아니기 때문이다. 예를 들어, N=6 일 경우, “2인 1닭” 세트를 3개 배달하면 총 3마리가 오는 반면, “3인 2닭” 세트를 2 개 배달하면 총 4마리까지 올 수도 있다. 태영이는 이미 답을 알고 있으나 계산하기 귀찮은 나머지 여러분들에게 프로그램을 만들라고 시켰다.

   치킨은 좋아하는 여러분들도 답이 궁금할 것이라고 생각되므로 이 문제를 풀어보자. N이 주어졌을 때 배달되는 치킨 수의 최솟값과 최댓값을 구하면 된다.

입력

첫째 줄에 사람의 수 N이 주어진다. N은 2016년에 재학 중이었던 카이스트 학생 수보다는 작거나 같은 2 이상의 정수이다.

출력

배달되는 치킨 수의 최솟값과 최댓값을 띄어쓰기로 구분하여 출력한다.

예제 입력 1

6

예제 출력 1

3 4

알고리즘 분류

• 수학
• 다이나믹 프로그래밍

코드

import sys
input = sys.stdin.readline

# 초기 상수 및 배열 선언
MXN = 10000  # 최대 사람 수를 나타내는 상수
dp = [[0, 0] for _ in range(MXN + 1)]  # 동적 계획법을 위한 2차원 배열
a, b, n = 1, 2, 0  # 현재 피보나치 수열 항의 앞 항, 뒷 항, 사람 수

# 입력 받기
n = int(input()) # 사람의 수

# DP 배열 초기화
for i in range(1, n + 1):
    dp[i][0] = float('inf')  # 최소 치킨 수를 무한대로 초기화

# DP 구현
while b <= n:
    for i in range(b, n + 1):
        # 최소치킨 수 갱신
        dp[i][0] = min(dp[i][0], dp[i - b][0] + a)
        # 최대치킨 수 갱신
        dp[i][1] = max(dp[i][1], dp[i - b][1] + a)
    b, a = b + a, b  # 다음 피보나치 수열 항으로 이동

# 결과 출력
print(dp[n][0], dp[n][1])  # 최소치킨 수와 최대치킨 수 출력

---

13164. 행복 유치원

문제

행복 유치원 원장인 태양이는 어느 날 N명의 원생들을 키 순서대로 일렬로 줄 세우고, 총 K개의 조로 나누려고 한다. 각 조에는 원생이 적어도 한 명 있어야 하며, 같은 조에 속한 원생들은 서로 인접해 있어야 한다. 조별로 인원수가 같을 필요는 없다.

이렇게 나뉘어진 조들은 각자 단체 티셔츠를 맞추려고 한다. 조마다 티셔츠를 맞추는 비용은 조에서 가장 키가 큰 원생과 가장 키가 작은 원생의 키 차이만큼 든다. 최대한 비용을 아끼고 싶어 하는 태양이는 K개의 조에 대해 티셔츠 만드는 비용의 합을 최소로 하고 싶어한다. 태양이를 도와 최소의 비용을 구하자.

입력

입력의 첫 줄에는 유치원에 있는 원생의 수를 나타내는 자연수 N(1 ≤ N ≤ 300,000)과 나누려고 하는 조의 개수를 나타내는 자연수 K(1 ≤ K ≤ N)가 공백으로 구분되어 주어진다. 다음 줄에는 원생들의 키를 나타내는 N개의 자연수가 공백으로 구분되어 줄 서 있는 순서대로 주어진다. 태양이는 원생들을 키 순서대로 줄 세웠으므로, 왼쪽에 있는 원생이 오른쪽에 있는 원생보다 크지 않다. 원생의 키는 109를 넘지 않는 자연수이다.

출력

티셔츠 만드는 비용이 최소가 되도록 K개의 조로 나누었을 때, 티셔츠 만드는 비용을 출력한다.

예제 입력 1

5 3
1 3 5 6 10

예제 출력 1

3

힌트

1조: 1, 3
2조: 5, 6
3조: 10

알고리즘 분류

• 그리디 알고리즘
• 정렬

코드

import sys
input = sys.stdin.readline

n, k = map(int, input().split())
arr = list(map(int, input().split()))

# 원생들의 키 차이를 나타내는 배열
cost = []
for i in range(1, len(arr)):
    cost.append(arr[i] - arr[i - 1])

# 한 조를 줄일 때 마다 가장 최소 비용을 더해주면 됨.
# n - k만큼 더하면 k조가 되는 최소 비용
cost.sort()
ans = 0
for i in range(n - k):
    c = cost[i]
    ans += c
print(ans)

---

4233. 가짜소수

문제

페르마의 소정리 (Fermat's little theorem)의 내용은 다음과 같다.
p가 소수일 때, 임의의 정수 a>1에 대해서, ap == a (mod p)가 성립한다.
즉, a를 p제곱한 뒤, p로 나눴을 때, 나머지는 a가 되는 것이다.
하지만, p가 소수가 아닌 경우에 어떤 정수 a에 대해서 위의 식을 만족하는 경우가 있다. 이때, p를 밑이 a인 가짜소수라고 한다. (모든 a에 대해서 식을 만족하는 수를 카마이클 수라고 한다)
p와 a가 주어졌을 때, p가 밑이 a인 가짜소수인지 아닌지 알아내는 프로그램을 작성하시오.

입력

입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, p와 a를 포함하고 있다. 입력의 마지막 줄에는 "0 0"이 주어진다. (2 < p ≤ 1,000,000,000, 1 < a < p)

출력

각 테스트 케이스에 대해서, p가 밑이 a인 가짜소수라면 yes를, 아니라면 no를 한 줄에 하나씩 출력한다.

예제 입력 1

3 2
10 3
341 2
341 3
1105 2
1105 3
0 0

예제 출력 1

no
no
yes
no
yes
yes

알고리즘 분류

• 수학
• 정수론
• 소수 판정
• 분할 정복을 이용한 거듭제곱
• 페르마의 소정리

코드

import sys
input = sys.stdin.readline

# 소수 여부를 확인하는 함수
def is_prime(n):
    if n < 2: # 2보다 작으면 소수가 아님
        return False
    for i in range(2, int(n**0.5) + 1):
        if n % i == 0: # 2부터 제곱근까지의 수로 나누어 떨어지면 소수가 아님
            return False
    return True

# 거듭제곱을 계산하는 함수
def power(x, n, MOD):
    ret = 1
    while n:
        if n & 1: # 지수가 홀수일 때
            ret = ret * x % MOD
        x = x * x % MOD
        n >>= 1  # 지수를 반으로 나눔
    return ret

while True:
    p, a = map(int, input().split())
    if p == 0 and a == 0:
        break

    # p가 소수가 아니고, a^p ≡ a (mod p) 인 경우를 확인
    is_carmichael = not is_prime(p) and power(a, p, p) == a

    # 결과 출력
    result = "yes" if is_carmichael else "no"
    print(result)

---

16562. 친구비

문제

19학번 이준석은 학생이 N명인 학교에 입학을 했다. 준석이는 입학을 맞아 모든 학생과 친구가 되고 싶어한다. 하지만 준석이는 평생 컴퓨터랑만 대화를 하며 살아왔기 때문에 사람과 말을 하는 법을 모른다. 그런 준석이에게도 희망이 있다. 바로 친구비다!

학생 i에게 Ai만큼의 돈을 주면 그 학생은 1달간 친구가 되어준다! 준석이에게는 총 k원의 돈이 있고 그 돈을 이용해서 친구를 사귀기로 했다. 막상 친구를 사귀다 보면 돈이 부족해질 것 같다는 생각을 하게 되었다. 그래서 준석이는 “친구의 친구는 친구다”를 이용하기로 했다.

준석이는 이제 모든 친구에게 돈을 주지 않아도 된다!

위와 같은 논리를 사용했을 때, 가장 적은 비용으로 모든 사람과 친구가 되는 방법을 구하라.

입력

첫 줄에 학생 수 N (1 ≤ N ≤ 10,000)과 친구관계 수 M (0 ≤ M ≤ 10,000), 가지고 있는 돈 k (1 ≤ k ≤ 10,000,000)가 주어진다.

두번째 줄에 N개의 각각의 학생이 원하는 친구비 Ai가 주어진다. (1 ≤ Ai ≤ 10,000, 1 ≤ i ≤ N)

다음 M개의 줄에는 숫자 v, w가 주어진다. 이것은 학생 v와 학생 w가 서로 친구라는 뜻이다. 자기 자신과 친구일 수도 있고, 같은 친구 관계가 여러 번 주어질 수도 있다.

출력

준석이가 모든 학생을 친구로 만들 수 있다면, 친구로 만드는데 드는 최소비용을 출력한다. 만약 친구를 다 사귈 수 없다면, “Oh no”(따옴표 제거)를 출력한다.

예제 입력 1

5 3 20
10 10 20 20 30
1 3
2 4
5 4

예제 출력 1

20

예제 입력 2

5 3 10
10 10 20 20 30
1 3
2 4
5 4

예제 출력 2

Oh no

알고리즘 분류

• 자료 구조
• 그래프 이론
• 그래프 탐색
• 분리 집합

코드

# 사용자로부터 입력을 받기 위해 표준 입력 모듈을 가져옵니다
from sys import stdin

# 부모 관계와 비용을 저장하기 위한 전역 변수
parents = []
charges = []

# x가 속한 집합의 대표(루트)를 찾기 위한 함수
def find(x: int) -> int:
    if parents[x] == x:
        return x
    # 경로 압축: 각 노드의 부모를 루트로 설정합니다
    parents[x] = find(parents[x])
    return parents[x]

# 두 집합을 비용을 기준으로 합치기 위한 함수
def union(x: int, y: int) -> None:
    x, y = find(x), find(y)
    # 랭크에 따른 합집합: 비용이 작은 집합을 비용이 큰 집합에 합칩니다
    if charges[x] < charges[y]:
        parents[y] = x
    else:
        parents[x] = y


# 표준 입력에서 입력을 읽기 위해 input() 함수를 재정의합니다
def input():
    return stdin.readline().rstrip()

# 친구의 수(n), 친구 관계의 수(m), 예산(k)을 입력으로 받습니다
n, m, k = map(int, input().split())

# 부모 관계와 비용 리스트를 초기화합니다
parents = list(i for i in range(n + 1))
charges = [0] + list(map(int, input().split()))

# 각 친구 관계에 대해 합집합을 수행합니다
for _ in range(m):
    v, w = map(int, input().split())
    union(v, w)

# 유일한 대표(부모)를 저장하기 위한 집합
friends = set()
cost = 0

# 유일한 대표의 비용을 합산하여 총 비용을 계산합니다
for i in range(1, n + 1):
    if find(i) not in friends:
        cost += charges[parents[i]]
        friends.add(parents[i])

# 총 비용이 예산을 초과하는지 확인하고 결과를 출력합니다
if cost > k:
    print("Oh no")
else:
    print(cost)