4.5.1 인덱스의 필요성
데이터를 빠르게 찾을 수 있는 하나의 장치!
인덱스 생성의 장단점
[장점]
- 검색 속도가 빨라 질수 있다.
- 시스템의 부하를 줄여 전체 시스템의 성능을 향상 시킨다.
[단점]
-
인덱스는 Database 공간을 차지 한다
-
인덱스 생성 시 많은 시간이 소요 될 수 있다.
-
데이터 변경 작업 시(Insert, Update, Delete) 성능이 나빠질 수 있다(빈번할 경우)
4.5.2 B-트리
B트리는 이진트리에서 발전되어 모든 리프 노드들이 같은 레벨을 가질 수 있도록 자동으로 밸런스를 맞추는 트리. 정렬된 순서를 보장하고, 멀티레벨 인덱싱을 통한 빠른 검색을 할 수 있어 DB에서 사용하는 자료구조 중 한 종류
자식 node의 개수가 2개 이상이며, node 내의 key가 1개 이상일 수 있다.
-
루트 노드
-
브랜치 노드
-
리프 노드
B-Tree의 조건은 다음과 같다. -
node의 key의 수가 k개라면, 자식 node의 수는 k+1개이다.
-
node의 key는 반드시 정렬된 상태여야 한다.
-
자식 node들의 key는 현재 node의 key를 기준으로 크기 순으로 나뉘게 된다.
-
root node는 항상 2개 이상의 자식 node를 갖는다. (root node가 leaf node인 경우 제외)
-
M차 트리일 때, root node와 leaf node를 제외한 모든 node는 최소⌈M2⌉⌈M2⌉, 최대MM개의 서브 트리를 갖는다.
-
모든 leaf node들은 같은 level에 있어야 한다.
B-Tree의 key 검색
그렇다면 원하는 값은 어떻게 찾을까?
이는 이진 탐색 트리에서와 비슷하다. 원하는 값을 K라고 가정하자.
- root node부터 탐색을 시작한다.
- node의 key를 순회하여 K가 존재하면 탐색을 종료한다.
- k가 존재하지 않는다면, 어떤 이웃한 두 key 사이에 K가 들어가는 경우 사이의 포인터를 통해 자식 node로 내려간다.
- leaf node까지 2~3을 반복한다.
예) 14라는 키를 검색해보자
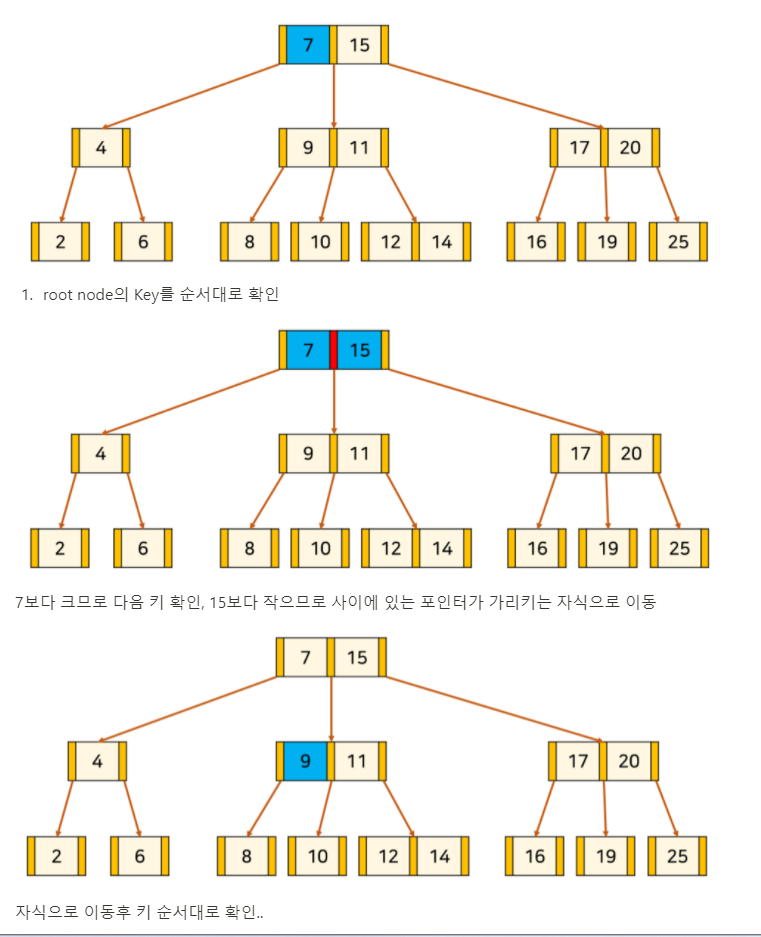

B-Tree의 key 삽입
-
빈 트리인 경우 root node를 만들어 K를 삽입한다.
root node가 가득 찬 경우 node를 분할하여 leaf node를 생성한다. -
K가 들어갈 leaf node를 검색 과정과 동일하게 탐색한다.
-
해당 leaf node에 자리가 남아있다면 정렬을 유지하도록 알맞은 위치에 삽입하고, leaf node가 꽉 차 있다면 K를 삽입한 후 해당 node를 분할한다
.4. node가 분할되는 경우 node의 중앙값을 기준으로 분할한다. 중앙값은 부모 node로 합쳐지거나 새로운 node로 생성되고, 중앙값을 기준으로 왼쪽의 key는 왼쪽 자식, 오른쪽의 key는 오른쪽 자식으로 생성된다.
예 13이라는 키 삽입
검색해서 부분까지 내려가고
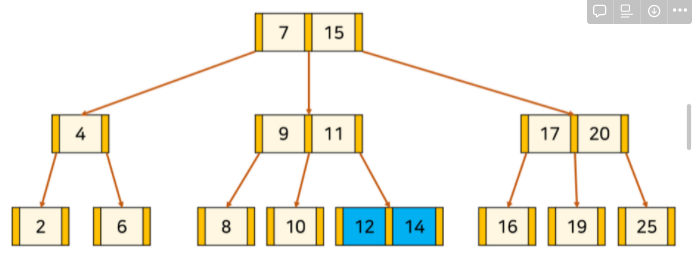
12와 14사이에 삽입
인덱스가 효율적인 이유와 대수확장성
인덱스는 효율적인 단계를 거쳐 모든 요소에 접근할 수 있는 균형잡힌 트리 구조와 트리 깊이의 대수확정성 때문입니다.
대수확장성이란 트리 깊이가 리프 노드 수에 비해 매우 느리게 성장하는 것을 의미합니다.
기본적으로 인덱스가 한 깊이씩 증가할 때마다 최대 인덱스 항목의 수는 4배씩 증가합니다.
트리깊이 인덱스 항목의 수

4.5.3 인덱스 만드는 방법
MySQL
-
클러스터형 인덱스
→ 데이블당 하나를 설정할 수 있다. -
프라이머리 키 옵션으로 기본키로 만들기
-
기보니로 만들지 않고 unique not null 옵션을 붙이기
-
세컨더리 인덱스
→create index.. 명령어
4.5.4 인덱스 최적화 기법
1) 인덱스는 비용이다.
인덱스는 두 번 탐색하도로 강요. 인덱스 리스트, 그 다음 컬렉션 순으로 탐색하기 때문이며, 관련 읽기 비용도 든다.
또한 컬렉션이 수정되었을 때 인덱스도 수정되어야 한다., 이때 B- 트리의 높이를 균형있게 조절하는 비용도 들고, 데이터를 효율적으로 조회할 수 있도록 분산시키는 비용도 든다.
2) 항상 테스팅하라
인덱스 최적화 기법은 서비스 특징에 따라 달라진다.
서비스에 사용하는 객체의 깊이, 테이블의 양 등이 다르기 때문!!!
explain) 함수를 통해 인덱스를 만들고, 쿼리를 보낸 이후에 테스팅을 하며 걸리는 시간을 최소화
3)복합 인덱슨는 같음, 정렬, 다중 값, 카디널리티 순이다.
어떠한 값과 같음을 비교하는 == 이나 equal이라는 쿼리가 있다면 제일 먼저 인덱스로 설정
정렬에 쓰는 필드라면 그 다음 인덱스로
다중 값을 출력해야 하는 필드, <이나 > 처럼 많은 값을 출력해야 하는 쿼리
유니크한 값의 정도를 카디널리티! 유니크가 높은 순서를 기반으로 인덱스 생성
예) age와 email → 당연히 email 이 더 유니크함! 그래서 email 인덱스를 먼저 생성

[참고링크]

