최소 공통 조상

최소 공통 조상이란?

최소 공통 조상(LCA, Lowest Common Ancestor)은 트리 구조에서 임의의 두 정점이 갖는 가장 가까운 조상 정점을 의미한다.

위와 같은 예시 트리 구조에서, 13, 15번 정점의 최소 공통 조상은 5번 정점이 된다.

13, 11번 정점의 최소 공통 조상은 1번 정점(Root)이 됩니다.

동작 순서

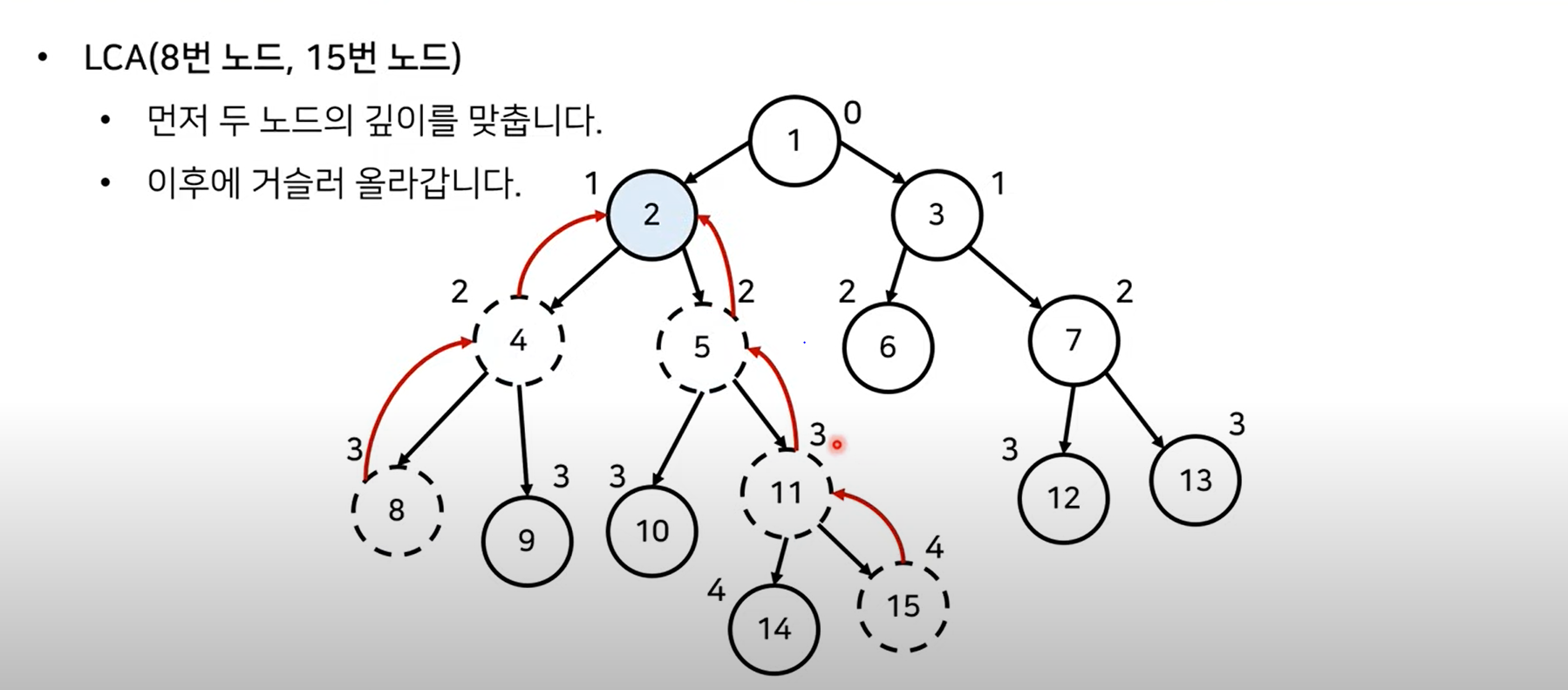
1. 모든 노드에 대한 깊이를 계산합니다.
2. 최소 공통 조상을 찾을 두 노드를 확인합니다.
3. 먼저 두 노드의 깊이가 동일하도록 거슬러 올라갑니다.
4. 부모가 같아질 때 까지 반복적으로 두 노드의 부모 방향으로 거슬러 올라갑니다.
5. 모든 LCA(a, b) 연산에 대하여 3 ~ 4번의 과정을 반복합니다.

그렇다면, 해당 풀이를 이용하여 문제를 해결하려고 할 때 필요한 것이 무엇이 있을까요?

1. 각 노드의 부모 노드를 저장한 배열
2. 각 노드의 레벨을 저장한 배열
3. 모든 노드를 탐고있는 트리

이때, ‘노드 객체에 지역 변수로서 깊이와 레벨을 저장해두면 되는 것이 아닌가’라는 생각을 가질 수 있지만, 실제로 두 노드의 번호만 입력 받았을 때 바로 바로 확인하기 위해서는 배열에 저장해서 확인하는 것이 효율적이다.

먼저, 1번 순서의 경우 트리를 형성하고 나서 루트 노드부터 탐색을 실시해야 할 것입니다. 탐색을 실시하면서 1번 배열과 2번 배열을 완성 시키면 그 이후부터는 1번, 2번 배열을 사용하여 LCA를 도출해내면 됩니다. 이때 중요한 점은 루트 노드를 알고 있어야 한다는 점입니다.

만약 루트 노드를 모른다면, 트리의 특성을 이용하여 루트 노드를 찾으면 됩니다.
=> 루트 노드를 제외한 모든 노드는 부모 노드를 가지고 있다.

코드

정상적으로 1번 배열과 2번 배열을 입력받았을 때, 코드는 다음과 같습니다.

int LCA(int[] parentList, int[] level, int n1, int n2) {

	// 1번
  if (level[n1] > level[n2]) {
    int temp = n1;
    n1 = n2;
    n2 = temp;
  }
	// 2번
   while (level[n1] != level[n2]) {
    n2 = parentList[n2];
  }
  // 3번
  while (n1 != n2) {
    n1 = parentList[n1];
    n2 = parentList[n2];
  }
  return n1;
}

참고로 LCA Algorithm에서 입력 값 n1, n2가 처음부터 일치할 경우 LCA(n1, n2) = n1 이라는 것에 주의합시다.

3번 조건문에서 n1 > 1을 안해줘도 되는 이유는 정상적인 트리라면 같은 높이에서 하나씩 올라간다면 결국 무조건 루트 노드에서 만나게 되어 있다.

먼저 n2의 깊이를 더 깊게 만들어 주기 위해 1번 과정을 거쳤다. 반복문 안에서 매번 비교 하는 것보다 미리 설정해두는 것이 효과적이다.

그 후, 2번 과정을 통해서 같은 층에 놓여있도록 만들어 줍니다. 이 과정에서 같은 노드가 선택 될 수도 있고, 다른 노드이지만 같은 레벨에 있는 노드일 수도 있습니다.

3번 과정을 통해서 최소 공통 조상을 찾습니다.

시간 복잡도

해당 풀이의 시간 복잡도의 경우 다음과 같습니다.

이 방법은 두 정점의 깊이에서부터 최대 root까지의 모든 정점을 선형으로 탐색해야 하므로, 시간 복잡도는 O(depth)가 됩니다. 만약, 편향트리를 만나게되면 엄청나게 많은 반복을 돌려줘야 할 수 있고, 중복 연산을 할 수도 있습니다. 편향 이진 트리의 경우 O(NM)이라는 시간 복잡도를 갖게 되어 범위가 더 크게 주어질 경우 해당 알고리즘은 느려질 것입니다.

따라서 개선된 방식의 LCA Algorithm을 사용합니다.

두가지 방식이 존재합니다.

1. LCA + DP: $O(MlogN)$
2. LCA + Segment Tree: $O(MlogN)$

LCA + DP

부모노드와 현재 노드의 거리가 100이면 일반적인 밥법으로는 100번의 반복을 통해 부모노드를 구해줘야 합니다. 하지만 $2^h$의 부모 노드를 알고 있다면 64 + 32 + 4 = 100으로 총 3번 만에 부모노드를 구할 수 있습니다.

이렇게 DP를 활용하면 연산 횟수를 급격하게 줄여줌으로서 시간복잡도를 $O(MlogN)$으로 단축시켜줍니다.

해당 방식은 Parent 배열을 2차원으로 두어, Parent[x][k] = “x번 정점의 $2^k$번째 조상 노드의 번호”로 둔다.

사실 이 부분이 가장 이해가 가지 않았습니다. 이것은 희소 테이블(Sparse table)이라는 개념을 이용하는 것인데, 저같은 경우 희소 테이블을 몰랐습니다. 그래서 희소 테이블이 무엇인지 정리 후 다시 진행하겠습니다.

희소 테이블(Sparse Table)

먼저 희소 테이블의 정의부터 살펴봅시다.

Sparse Table이란 전체 원소들 중 임의의 원소에 대해, 해당 원소에 N번째 앞에 있는 원소를 빠르게 찾기 위해 사용하는 자료구조이다.

예시를 통해서 살펴봅시다.

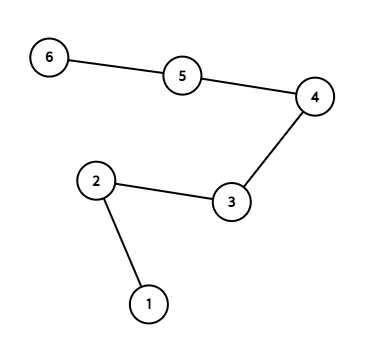
1번 정점에서부터 6번 정점으로 이동한다고 생각해 봅시다.

보통 일반적인 방식이 모든 정점을 거쳐서 탐색을 하는 것입니다.

• O(5) : 1 ⇒ 2 ⇒ 3 ⇒ 4 ⇒ 5 ⇒ 6

하지만, 이때 희소 테이블을 사용하면 $O(logN)$만에 갈 수 있습니다.

• O(log5) : 1 ⇒ 5 ⇒ 6

어떻게 위와 같은 방식을 사용할 수 있는 것일까요?

해당 방식을 정확히 이해하려면 다음 전제 조건을 기억하고 있어야 합니다.

모든 숫자는 $2^k$의 숫자들의 합으로 만들 수 있습니다.
⇒ 모든 숫자는 2진수의 형태로 변환이 가능합니다.

즉, 6까지 도달하기 위해서 5회 이동 하므로 $5 = (2^2 + 1)$ 의 형태로 표현되어 진 것입니다.

이것을 2차 배열을 이용하여 하나의 수식으로 표현되어 질 수 있습니다.

parent[node][pow] = parent[parent[node][pow - 1]][pow - 1]

사실 이 코드를 이해하는데 고생을 했습니다..

차근차근 정리해 보겠습니다.

먼저, 위에서도 보았다싶히 parent 배열은 자신의 부모 노드를 저장해두는 배열 입니다.

표를 하나 만들어 보겠습니다.

그림 1과 같이 편향그래프라고 생각하고 Node가 1 ~ 16 까지 존재한다고 생각해 봅시다.

처음 parent[node][0] 에는 자신의 부모 노드를 탐색하는 과정에서 채워 줄 것입니다. 위에서 일반적인 LCA를 구할 때 처럼 말입니다.

	k = 0
parent[1][0]	1
parent[2][0]	1
parent[3][0]	2
…	…
…	…
…	…
parent[16][0]	15

이와 같이 채워질 것입니다.

그리고 parent[node][1]을 구할 때는 앞서 구했던 부모 노드의 부모 노드를 참조 합니다.

parent[node][1] = parent[parent[node][1 - 1]][1 - 1];

	k = 0	k = 1
parent[1][k]	1	1
parent[2][k]	1	1
parent[3][k]	2	1
parent[4][k]	…	2
…	…
parent[15][k]	14
parent[16][k]	15	14

이 과정은 다음과 같이 생각해 볼 수 있다. 앞서 우리는 k = 0에서 부모 노드를 입력해 놓았습니다.

즉, parent[node][1 - 1]의 경우 결국 부모 노드를 가져오는 것입니다. 그 후 그 노드의 부모 노드를 가져오는 과정입니다.

결국, 부모 노드 → 부모 노드를 가져온 것입니다.

node가 3일때 과정을 살펴보면 다음과 같습니다.

• parent[3][1] = parent[parent[3][0]][0] = parent[2][0] = 1

다음 k = 2일 때가 문제이다.

	k = 0	k = 1	k = 2
parent[1][k]	1	1	1
parent[2][k]	1	1	1
parent[3][k]	2	1	1
parent[4][k]	…	2	1
…	…	…	…
parent[15][k]	14	13	11
parent[16][k]	15	14	12

이것만 보면 왜 14 → 13 으로 가다가 13 → 11로 가는 것인지 도무지 이해가 안됐습니다.

좀 더 표를 완성시켜 보겠습니다.

	k = 0	k = 1	k = 2
parent[1][k]	1	1	1
parent[2][k]	1	1	1
parent[3][k]	2	1	1
parent[4][k]	3	2	1
parent[5][k]	4	3	1
parent[6][k]	5	4	2
parent[7][k]	6	5	3
parent[8][k]	7	6	4
parent[9][k]	8	7	5
parent[10][k]	9	8	6
parent[11][k]	10	9	7
parent[12][k]	11	10	8
parent[13][k]	12	11	9
parent[14][k]	13	12	10
parent[15][k]	14	13	11
parent[16][k]	15	14	12

여기서 node가 6일 때를 살펴보자.

먼저, 식부터 쭉 적어보자면 다음과 같습니다.

• parent[6][2] = parent[parent[6][1]][1] = parent[4][1] = 2

먼저 parent[6][1]의 경우 우리는 부모 노드 → 부모노드의 과정을 거친 부분을 구해놓았습니다.

즉, 거기서 다시 또 해당 노드의 부모 노드 → 부모 노드를 가져온 것입니다.

즉, (현재 노드 의 부모 노드 → 부모 노드)의 부모 노드 → 부모 노드를 가져온 것입니다.

즉, k = 2니깐 $2^2$만큼의 부모 노드를 가져와서 배열에 입력해 놓는 것입니다.

이런 방식으로 진행되어 진다면, k = 3일 때는 어떻게 될까요?

$2^3= 8$칸 앞에 있는 부모 노드를 parent[node][3]에 입력해 놓을 것입니다.

이것이 바로 희소 테이블입니다.

해당 식을 다시 한번 쓰자면 다음과 같습니다.

parent[node][pow] = parent[parent[node][pow - 1]][pow - 1]

자 이제 본격적으로 DP를 활용한 LCA를 정리하도록 하겠습니다.

동작 순서

1. 모든 노드를 탐색하면서 노드에 대한 깊이, 부모 노드에 대한 정보를 담습니다.
2. parent[node][0]에 모든 정보를 채워둔 것을 토대로 parent[node][k]에 대한 정보를 채워 넣습니다.
   1. $k = 1 : 2^k ≥ N$ 을 만족하는 최솟값 k를 구하여 범위를 설정 후 반복문 진행
   2. node = 1 ~ 마지막 Node까지 반복문을 진행한다.
   3. Sparse Table 완성 시키기
3. Sparse Table을 이용하여 두 노드를 같은 레벨로 맞춥니다.
   1. 이때 위에서 봤다싶히 node1, node2 중에 하나를 선택해서 무조건 한 쪽을 하위노드로 만들고 진행하면 반복문 안에 조건문을 안넣기 때문에 더 빠릅니다.
   2. k - 1부터 0까지 반복문을 진행하면서 높이의 차이를 0으로 만든다고 생각하고 하위 노드를 계속해서 옮겨 줍니다.
4. 같은 레벨에 맞추고 나서부터는 다시 Sparse Table과 k - 1 ~ 0 까지 반복문을 사용하여 이번에는 최소 공통 조상 직전 노드 까지 높이(거리) 차이를 0으로 하듯이 노드 위치를 바꿔가며 확인해 줍니다.

Sparse Table 만드는 과정만 코드로 보면 다음과 같습니다.

void set_spaTable(int[][] parent, int N, int k) {
  for (int i = 1; i < k; i++) {
    for (int node = 1; node <= N; node++) {
      parent[node][i] = parent[parent[node][i - 1]][i - 1];
    }
  }
}

Sparse Table을 LCA에서 이용하는 과정은 다음과 같습니다.

int LCA(int n1, int n2, int[][] parent, int[] depth, int k) {

  if (depth[n1] > depth[n2]) {
    int temp = n1;
    n1 = n2;
    n2 = temp;
  }

  for (int i = k - 1; i >= 0; i--) {
    if (depth[n2] - depth[n1] >= Math.pow(2,i)) {
      n2 = parent[n2][i];
    }
  }

  if (n1 == n2) return n1;

  for (int i = k - 1; i>= 0; i--) {
    if (parent[n1][i] != parent[n2][i]) {
      n1 = parent[n1][i];
      n2 = parent[n2][i];
    }
  }

  return parent[n1][0];
}

LCA + Segment Tree

해당 방식은 전위 순회의 특징을 이해하고 사용해야 하는 방식입니다.

임의의 두 노드의 최소 조상 트리를 구할 때 전위 순환을 하면 임의의 두 노드 모두를 방문 하는 사이에 무조건 최소 공통 조상 노드를 방문하게 된다.

전위 순회 특징

먼저 다음의 트리를 보면서 이해해 보겠습니다.

해당 트리에서 임의의 두 노드를 6과 5라고 해보겠습니다.

전위 순회를 한다면 다음과 같은 순서로 방문할 것입니다.

1 -> 2 -> 4 -> 6 -> 4 -> 2 -> 5 -> 2 -> 1 -> 3 -> 1

이렇게 방문합니다.

방문 순서에 강조해놓은 것처럼 노드 6 과 5를 방문하는 사이에 최소 공통 조상 노드인 2가 있는 것을 확인할 수 있습니다.

다른 예시도 살펴봅시다.

6과 3을 생각해 본다면, 3을 방문하기 직전 둘의 최소 공통 조상인 1이 있는 것을 확인할 수 있습니다.

2와 6을 생각한다면, 2가 최소 공통 조상에 해당하므로 노드 2를 방문할 때 방문한 것으로 생각하면 됩니다.

왜 이런 현상이 나오는 걸까요?

전위 순회는 root -> left -> right 순으로 방문하는 특징을 가지고 있습니다.

만약 임의의 두 노드가 한 줄에 치우쳐서 일자로 있다면(노드 2와 6처럼) 이미 둘 중 하나의 노드가 최소 공통 조상임을 알 수 있습니다.

다른 경우라면 임의의 두 노드를 포함하는 서브 트리를 생각할 수 있는데 전위 순회 특징상 돌아오는 사이에 무조건 Root를 방문하기 때문에 이러한 특징을 보여주는 것입니다.

세그먼트 트리 초기화

세그먼트 트리의 경우 먼저 nodeL(start), nodeR(end)라는 범위 변수가 존재하고 노드에 들어가는 value가 존재합니다.

• nodeL, nodeR: 전위 순회할 때 해당 노드를 방문한 순서
• value: (해당 노드의 레벨, 노드 번호)

그리고 해당 세그먼트 트리는 최솟값을 이용합니다.

왜 이렇게 사용하는지 아래에 차근차근 설명하도록 하겠습니다.

해당 예시를 보면서 설명을 들겠습니다.

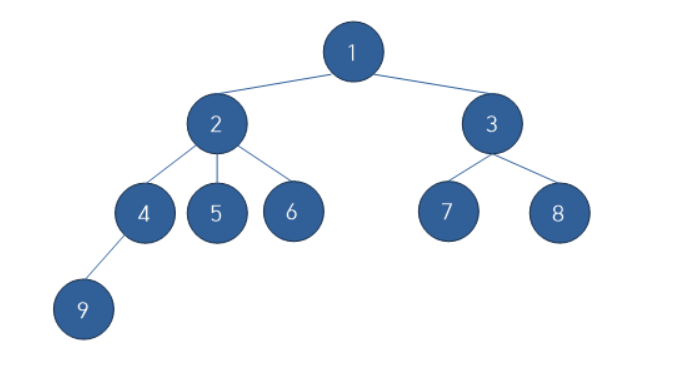
해당 트리를 전위 순회한다고 했을 때,

(해당 노드의 레벨, 노드 번호)를 저장한다고 해봅시다. 다음과 같은 순서로 나올 것입니다.

(0,1) (1,2) (2,4) (3,9) (2,4) (1,2) (2,5) (1,2) (2,6) (1,2) (0,1) (1,3) (2,7) (1,3) (2,8) (1,3) (0,1)

이것들을 노드로 만들어서 세그먼트 트리의 리프노드로 만들어 줍니다. 그러면서 높이의 최솟값을 부모 노드로 저장해가며 Min Segment Tree를 완성시켜주면 됩니다.

방문 순서같은 경우 배열에 저장해두어서 query()함수에서 활용하면 됩니다.

방문 순서 배열은 다음과 같을 것입니다.

node 번호	1	2	3	4	5	6	7	8	9
방문 순서	1	2	12	3	7	9	13	15	4

두 노드를 받아서 방문 순서를 쿼리안에 넣고 방문 순서를 맞춰서 최솟값을 찾으면 그것이 곧 최소 공통 조상 노드에 해당할 것입니다.

예를 들어, 만약, 노드 4와 6의 LCA를 구한다면 4와 6의 방문순서 3, 9를 nodeL과 nodeR로 두고 start와 end를 조절해가며 query()를 이용한다면 최솟값(최소 공통 조상)을 구할 수 있을 것입니다.

(0,1) (1,2) (2,4) (3,9) (2,4) (1,2) (2,5) (1,2) (2,6) (1,2) (0,1) (1,3) (2,7) (1,3) (2,8) (1,3) (0,1)

강조한 위치에서 min값을 찾을 것이고 거기서 (1,2)를 꺼내올 것입니다. 따라서, LCA가 2라는 것을 알 수 있습니다.

코드

코드의 경우 11438번: LCA 2 해당 문제를 기준으로 풀이를 올려놨습니다.

// Using DP 

import java.io.*;
import java.util.ArrayList;
import java.util.StringTokenizer;

public class Main {
  public static void main(String[] args) throws IOException {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
    StringTokenizer st;

    int N = Integer.parseInt(br.readLine());

    ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
    for (int i = 0; i < N + 1; i++) {
      graph.add(new ArrayList<>());
    }

    for (int i = 0; i < N - 1; i++) {
      st = new StringTokenizer(br.readLine());
      int n1 = Integer.parseInt(st.nextToken());
      int n2 = Integer.parseInt(st.nextToken());

      graph.get(n1).add(n2);
      graph.get(n2).add(n1);
    }

    boolean[] isVisited = new boolean[N + 1];
    int[] depth = new int[N + 1];
    int k = (int)Math.ceil(Math.log(N) / Math.log(2)) + 1;
    int[][] parent = new int[N + 1][k];

    DFS(graph, isVisited, depth, parent, 0, 1);

    set_spaTable(parent, N, k);

    int M = Integer.parseInt(br.readLine());

    for (int i = 0; i < M; i++) {
      st = new StringTokenizer(br.readLine());
      int n1 = Integer.parseInt(st.nextToken());
      int n2 = Integer.parseInt(st.nextToken());

      bw.write(LCA(n1, n2, parent, depth, k) + "\n");
    }

    bw.flush();
    bw.close();
  }

  static int LCA(int n1, int n2, int[][] parent, int[] depth, int k) {

    if (depth[n1] > depth[n2]) {
      int temp = n1;
      n1 = n2;
      n2 = temp;
    }

    for (int i = k - 1; i >= 0; i--) {
      if (depth[n2] - depth[n1] >= Math.pow(2,i)) {
        n2 = parent[n2][i];
      }
    }

    if (n1 == n2) return n1;

    for (int i = k - 1; i>= 0; i--) {
      if (parent[n1][i] != parent[n2][i]) {
        n1 = parent[n1][i];
        n2 = parent[n2][i];
      }
    }

    return parent[n1][0];
  }
  static void DFS(ArrayList<ArrayList<Integer>> graph, boolean[] isVisited, int[] depth, int[][] parent, int curDepth, int node) {
    isVisited[node] = true;
    depth[node] = curDepth;

    for (int childNode : graph.get(node)) {
      if (!isVisited[childNode]) {
        parent[childNode][0] = node;
        DFS(graph, isVisited, depth, parent, curDepth + 1, childNode);
      }
    }
  }
  static void set_spaTable(int[][] parent, int N, int k) {
    for (int i = 1; i < k; i++) {
      for (int node = 1; node <= N; node++) {
        parent[node][i] = parent[parent[node][i - 1]][i - 1];
      }
    }
  }
}

// Using Segment Tree

import java.io.*;
import java.util.ArrayList;
import java.util.StringTokenizer;

public class Main {
  static int INF = Integer.MAX_VALUE;
  public static void main(String[] args) throws IOException {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
    StringTokenizer st;

    int N = Integer.parseInt(br.readLine());

    ArrayList<ArrayList<Integer>> graph = new ArrayList<>();

    for(int i = 0; i < N + 1; i++) graph.add(new ArrayList<>());

    for (int i = 1; i < N; i++) {
      st = new StringTokenizer(br.readLine());

      int n1 = Integer.parseInt(st.nextToken());
      int n2 = Integer.parseInt(st.nextToken());

      graph.get(n1).add(n2);
      graph.get(n2).add(n1);
    }

    boolean[] isVisited = new boolean[N + 1];
    int[] level = new int[N + 1];

    ArrayList<Integer[]> leafNode = new ArrayList<>();

    // DFS + Segment Tree 전처리
    DFS(graph, isVisited, level, 1, 1, leafNode);


    // Tree Size 결정
    int size = leafNode.size();
    int h = (int)Math.ceil(Math.log(size) / Math.log(2));
    int tree_size = 1 << (h + 1);
    // Initialize Segment Tree
    Integer[][] tree = new Integer[tree_size][2];

    // 순서를 0 ~ size - 1까지
    initST(tree, 1, 0, size - 1, leafNode);

    // 입력 받은 Node 번호 -> 해당 Node 최초 방문 순서로 바꿔주는 Table 생성
    int[] visitedOrder = new int[N + 1];
    for (int i = 0 ; i < size; i++) {
      int nodeIdx = leafNode.get(i)[1];
      if (visitedOrder[nodeIdx] == 0) {
        visitedOrder[nodeIdx] = i;
      }
    }

    // Find LCA
    int M = Integer.parseInt(br.readLine());

    for (int i = 0 ; i < M; i++) {
      st = new StringTokenizer(br.readLine());

      int n1 = Integer.parseInt(st.nextToken());
      int n2 = Integer.parseInt(st.nextToken());

      if (n1 == n2)  {
        bw.write(n1+"\n");
        continue;
      }

      int orderN1 = visitedOrder[n1];
      int orderN2 = visitedOrder[n2];

      if (orderN1 > orderN2) {
        int temp = orderN1;
        orderN1 = orderN2;
        orderN2 = temp;
      }
      Integer[] lcaNode = query(tree, 1, 0 , size - 1, orderN1, orderN2);
      bw.write(lcaNode[1]+"\n");
    }
    bw.flush();
    bw.close();
  }

  static void DFS(ArrayList<ArrayList<Integer>> graph, boolean[] isVisited, int[] level, int node, int curLevel, ArrayList<Integer[]> leafNode) {
    Integer[] leaf = {curLevel, node};
    leafNode.add(leaf);

    isVisited[node] = true;
    level[node] = curLevel;

    for (int childNode : graph.get(node)) {
      if (!isVisited[childNode]) {
        DFS(graph, isVisited, level, childNode, curLevel + 1, leafNode);
        leafNode.add(leaf);
      }
    }
  }

  static void initST(Integer[][] tree, int node, int start, int end, ArrayList<Integer[]> leafNode) {
    if (start == end) {
      tree[node] = leafNode.get(start);
    }
    else {
      int mid = (start + end) / 2;
      initST(tree, node * 2, start, mid, leafNode);
      initST(tree, node * 2 + 1, mid + 1, end, leafNode);
      // 두 노드의 Level 비교
      if (tree[node * 2][0] <= tree[node * 2 + 1][0]) {
        tree[node] = tree[node * 2];
      } else {
        tree[node] = tree[node * 2 + 1];
      }
    }
  }

  static Integer[] query(Integer[][] tree, int node, int start, int end, int nodeL, int nodeR) {
    if (nodeL <= start && end <= nodeR) {
      return tree[node];
    }
    if (end < nodeL || nodeR < start) {
      return new Integer[]{INF, INF};
    }
    int mid = (start + end) / 2;
    Integer[] lNode = query(tree, node * 2, start, mid, nodeL, nodeR);
    Integer[] rNode = query(tree, node * 2 + 1, mid + 1, end, nodeL, nodeR);
    if (lNode[0] > rNode[0]) {
      return rNode;
    }
    else {
      return lNode;
    }
  }
}

다만, 해당 풀이같은 경우 이상하게도 세그먼트 트리가 시간이 한참 오래걸렸습니다..

일단 맨 위의 풀이가 Segment Tree를 활용한 풀이라고 보면 되고, 4번째 풀이가 DP를 활용한 풀이 입니다. 3번째 풀이의 경우 Segment Tree풀이지만, BufferedWriter가 아닌 System.out.println을 사용한 경우입니다.

출력 형태만으로도 굉장히 느려진 걸 보고 솔직히 놀랐습니다..

다른 곳을 보니깐 보통 Segment Tree가 더 빠르다고 하는데 혹시 코드 최적화 가능한 부분이 보이면 댓글로 남겨주시면 감사하겠습니다 ^^

---

Reference

• [알고리즘] 최소 공통 조상 LCA 트리 - DP & 세그먼트 트리 (Java)
• LCA(Lowest Common Ancestor) 최소 공통 조상 알고리즘 : 네이버 블로그