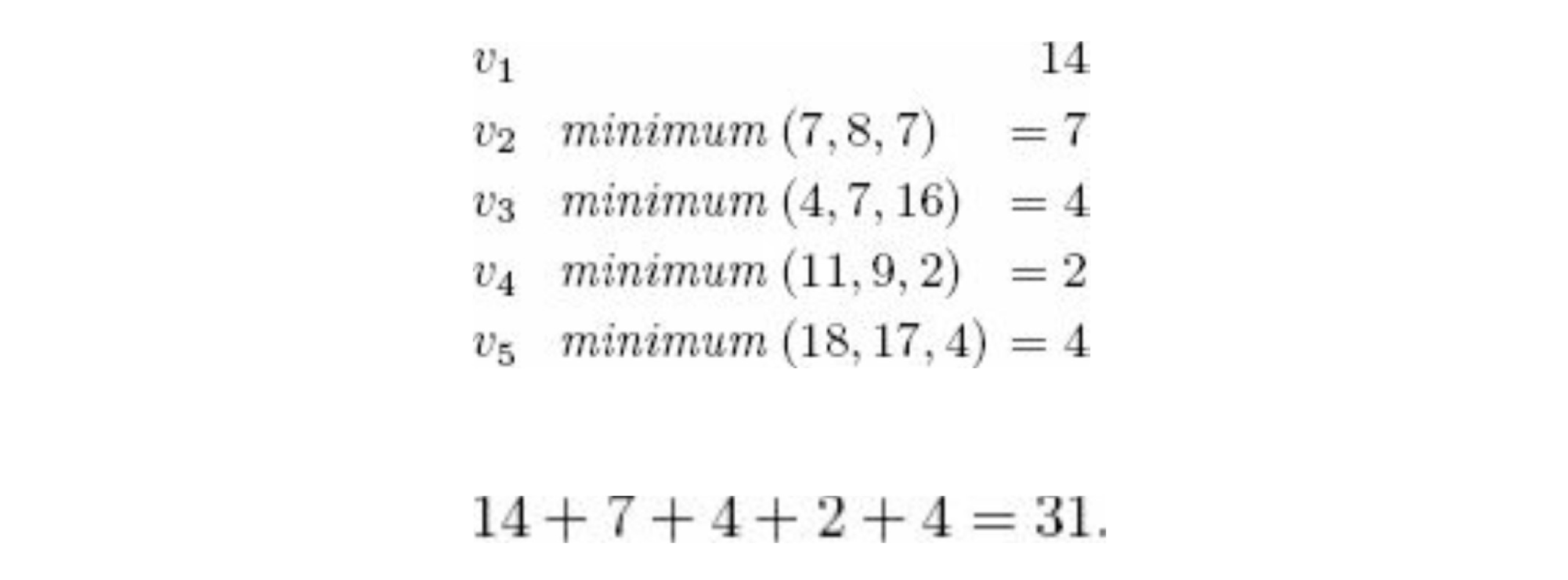Branch and Bound

• Backtracking Algorithm과 마찬가지로 State Space Tree를 사용하지만 Traversing 순서를 다르게 적용
• 차이점
  • Tree Traversal 제한 X (Breadth-First or Best-First)
  • Optimization Problem에만 사용
• Tree의 각 Node에서 Bound를 검사하여 Promising 여부 판단
  • Bound: Node를 확장했을 때 얻을 수 있는 Solution 값
  • Bound 값이 지금까지 발견한 최적의 Solution보다 못하면 Nonpromising으로 판단
• Backtracking으로 좋은 결과를 내기 어렵다면 Branch & Bound 역시 마찬가지
• Worst Case시 Exponential-Time Algorithm이지만 많은 경우 효율적으로 동작

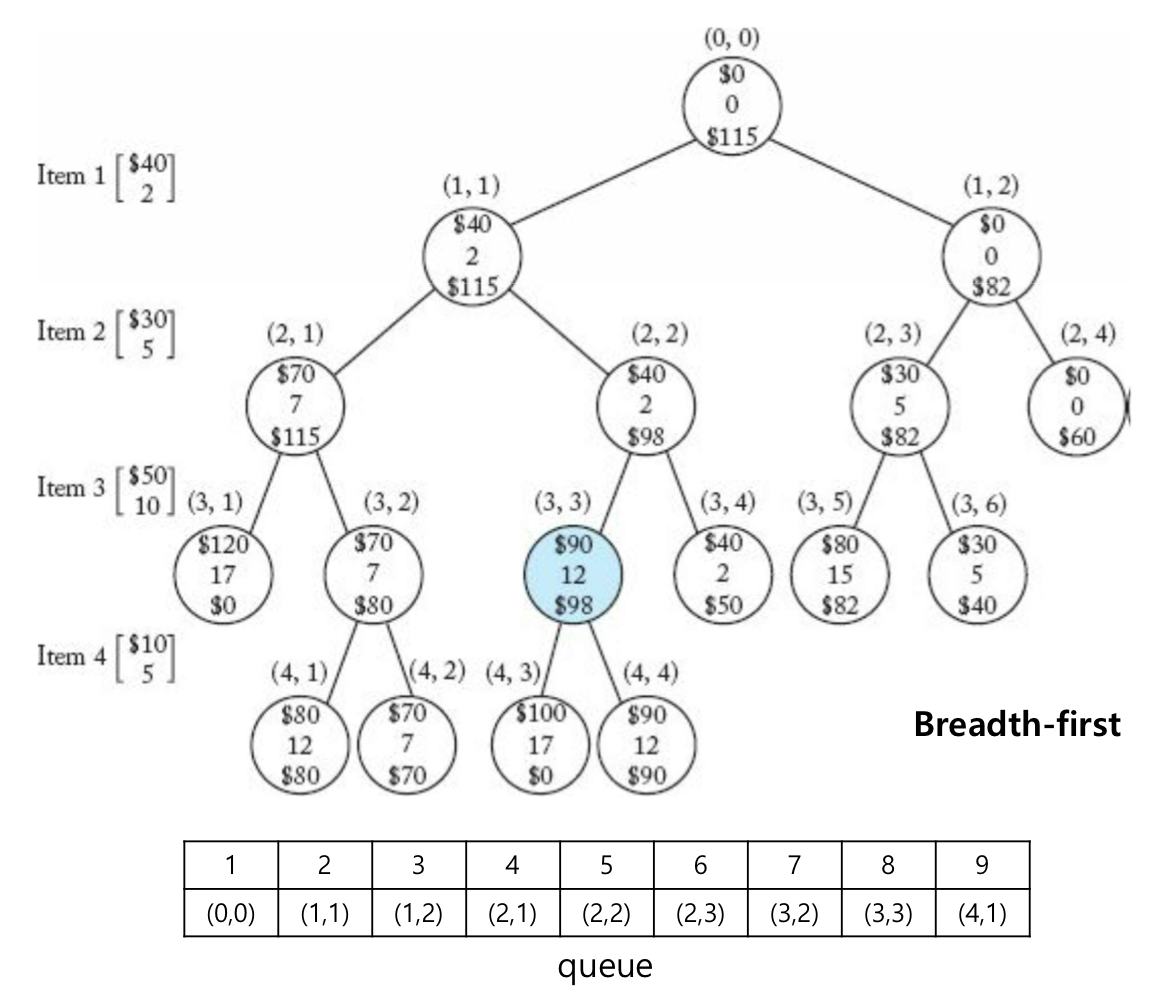
0-1 Knapsack Problem

• $n = 4$, $W = 16$, $wᵢ$ 는 아래와 같다

$i$	$pᵢ$	$wᵢ$	$pᵢ/wᵢ$
1	$40	2	$20
2	$30	5	$6
3	$50	10	$5
4	$10	5	$2

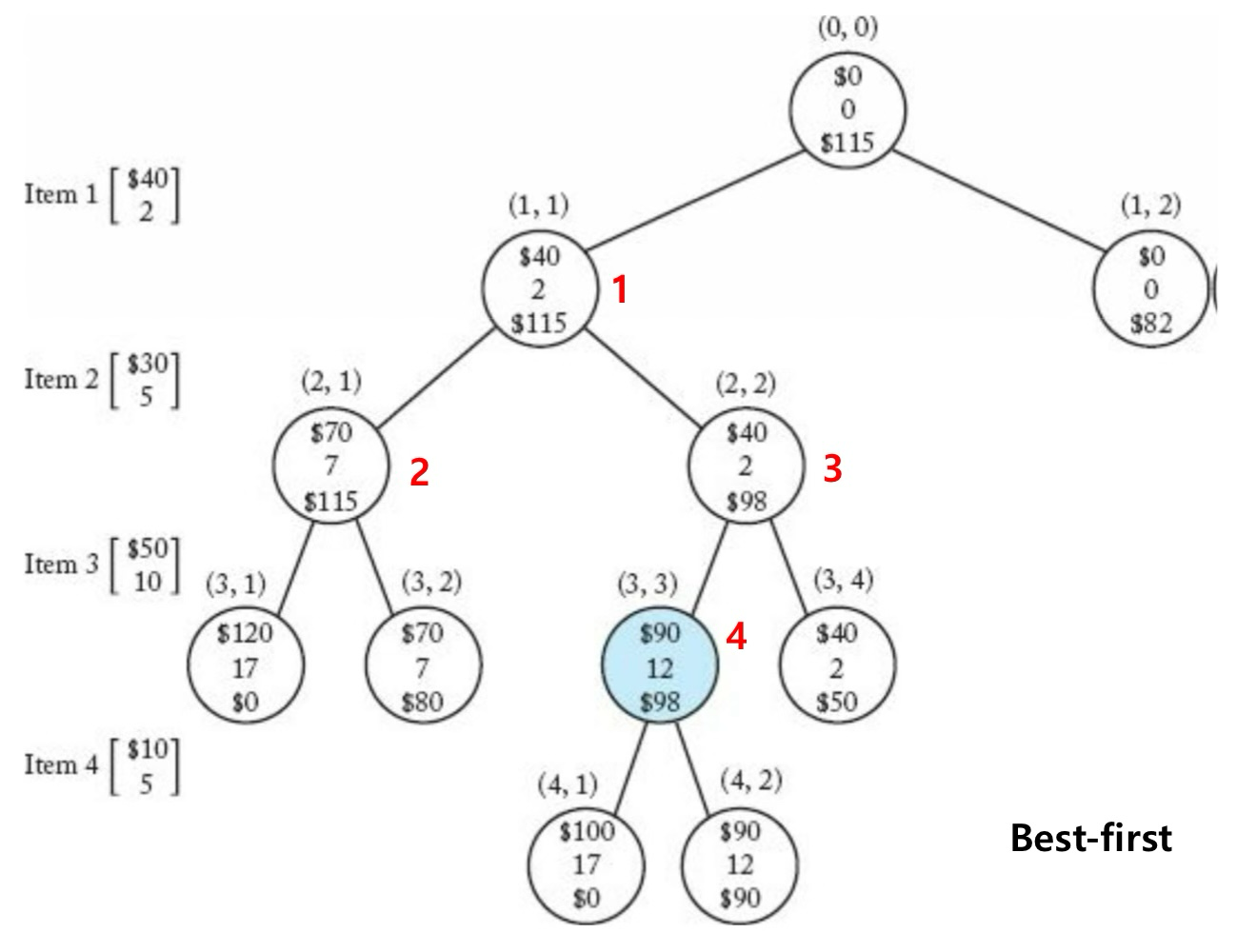
• Bound 계산
  • (0, 0) : 115($W = 16$) = 40($w₁ = 2$) + 30($w₂ = 5$) + 45($w₃ = 10 * 0.9 = 9$)
  • (1, 1) : 115($W = 16$) = 40($w₁ = 2$) + 30($w₂ = 5$) + 45($w₃ = 10 * 0.9 = 9$)
  • (1, 2) : 82($W = 16$) = 30($w₂ = 5$) + 50($w₃ = 10$) + 2($w₄ = 5 * 0.2 = 1$)
  • (2, 1) : 115($W = 16$) = 40($w₁ = 2$) + 30($w₂ = 5$) + 45($w₃ = 10 * 0.9 = 9$)
  • (2, 2) : 98($W = 16$) = 40($w₁ = 2$) + 50($w₃ = 10$) + 8($w₄ = 5 * 0.8 = 4$)
  • (2, 3) : 82($W = 16$) = 30($w₂ = 5$) + 50($w₃ = 10$) + 2($w₄ = 5 * 0.2 = 1$)
  • (2, 4) : 60($W = 15$) = 50($w₃ = 10$) + 10($w₄ = 5$)

Best First Search

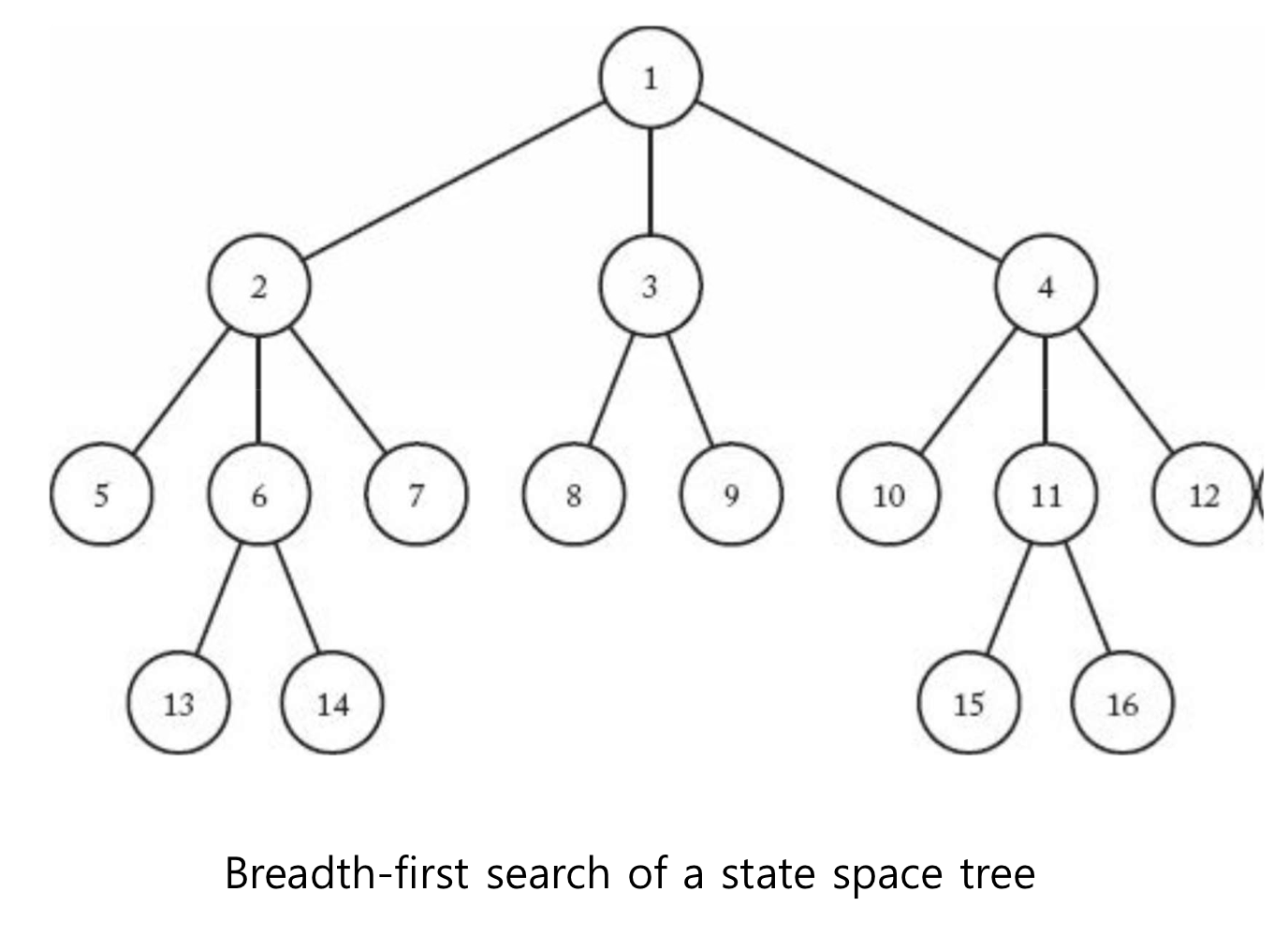
• State Space Tree를 탐색할 때 Breadth-First Search 또는 Best-First Search 수행
  → Best-First Search가 조금 더 효율적
• 여러 Node들의 Bound를 계산한 후 비교하여 최적의 Bound 값을 갖는 Node부터 탐색
  → Best-First Search
• Breadth-First Search의 구현은 Queue, Best-First Search의 구현은 Heap Queue 구조
  → Node를 Heap Queue에 추가하면 Bound 크기 순으로 자동 정렬
• 위 예제의 Node 방문 횟수 대비 6회 줄일 수 있음

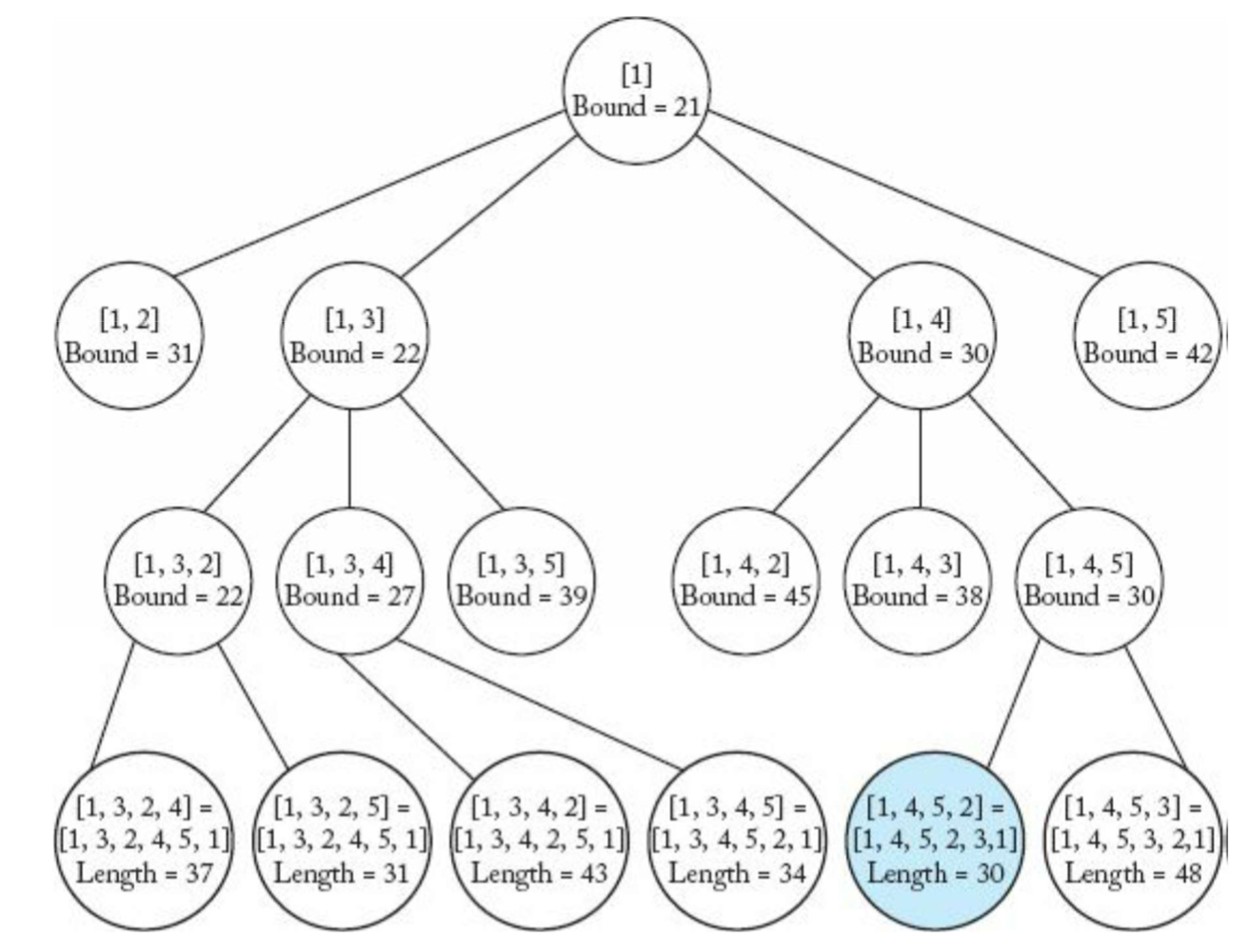
Traveling Salesperson Problem

• Best-First Search를 이용하여 문제 해결
  • Promising 조건: Bound가 현재의 Minimum Tour Length보다 작을 때
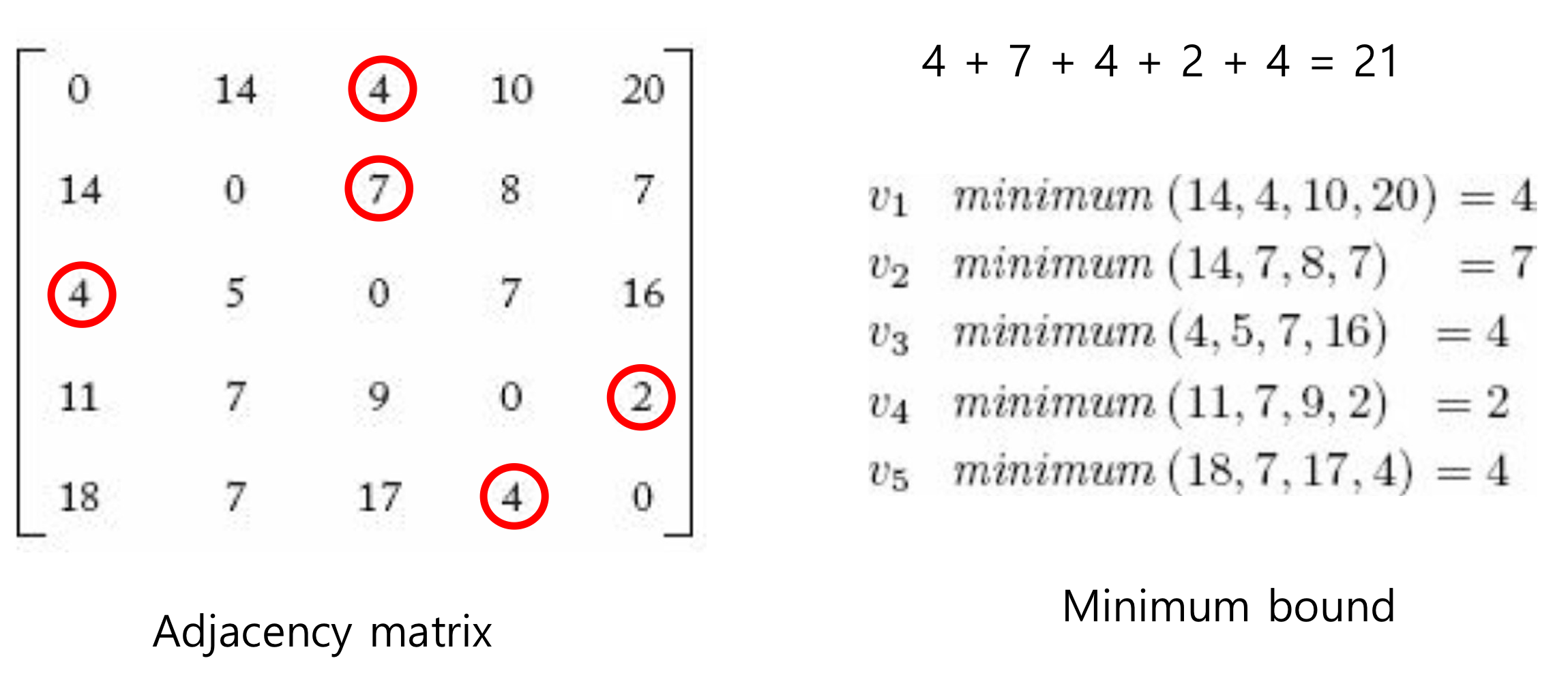
  • Bound: 현재 Vertex에서 계속 확장했을 때 얻을 수 있는 최소 Length
  • Tour Length의 최솟값은 각 Vertex의 Minimum Bound의 합(21)보다 크다.

• 만약 [$v₁, v₂$]를 선택했다면 Bound는 31
  • $v₁$ → $v₂$의 Length는 14
  • 나머지 Vertex들에서 $v₂$는 $v₁$과 연결된 Length를 제거, 다른 Vertex들은 $v₂$와 연결된 Length 제거 후 Minimum Length를 재계산

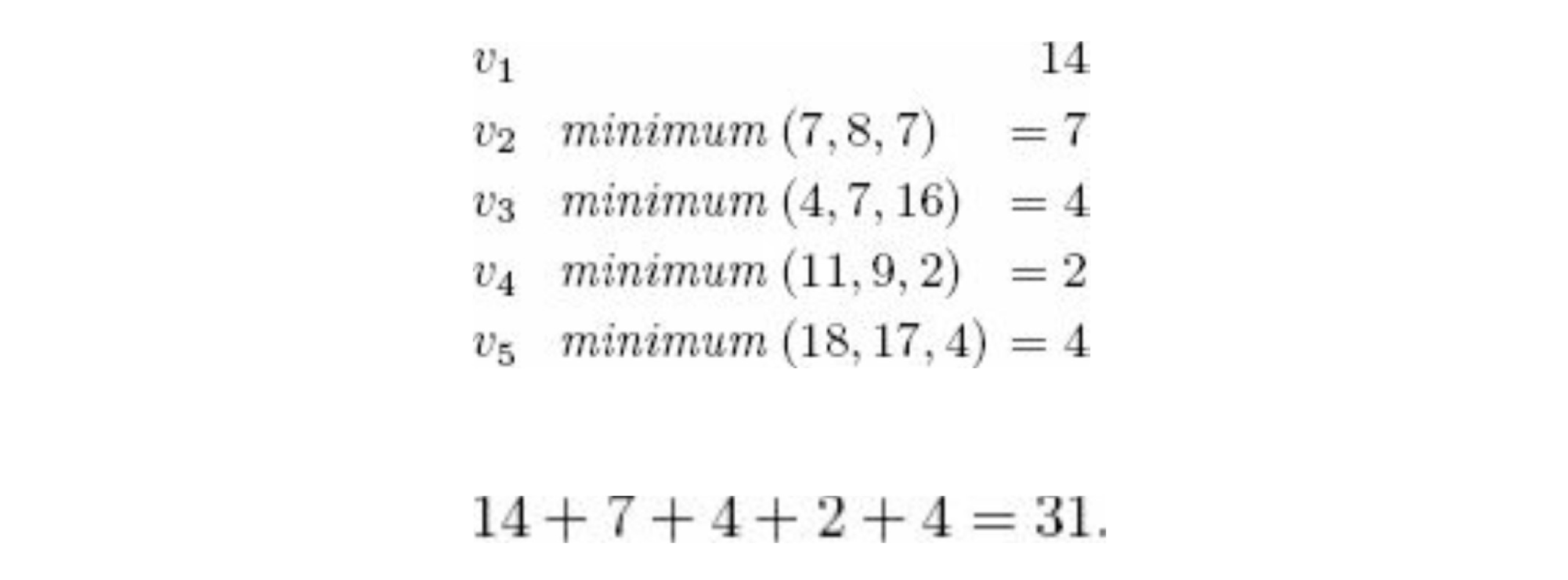
• 만약 [$v₁, v₂, v₃$]를 선택했다면 Bound는 34
  • $v₁$ → $v₂$의 Length는 14, $v₂$ → $v₃$의 Length는 7
  • $v₃$은 $v₁$, $v₂$와 연결된 Length를 제거, 다른 Vertex들은 $v₂$, $v₃$과 연결된 Length 제거 후 Minimum Length를 재계산