Graph Coloring

m-Coloring Problem

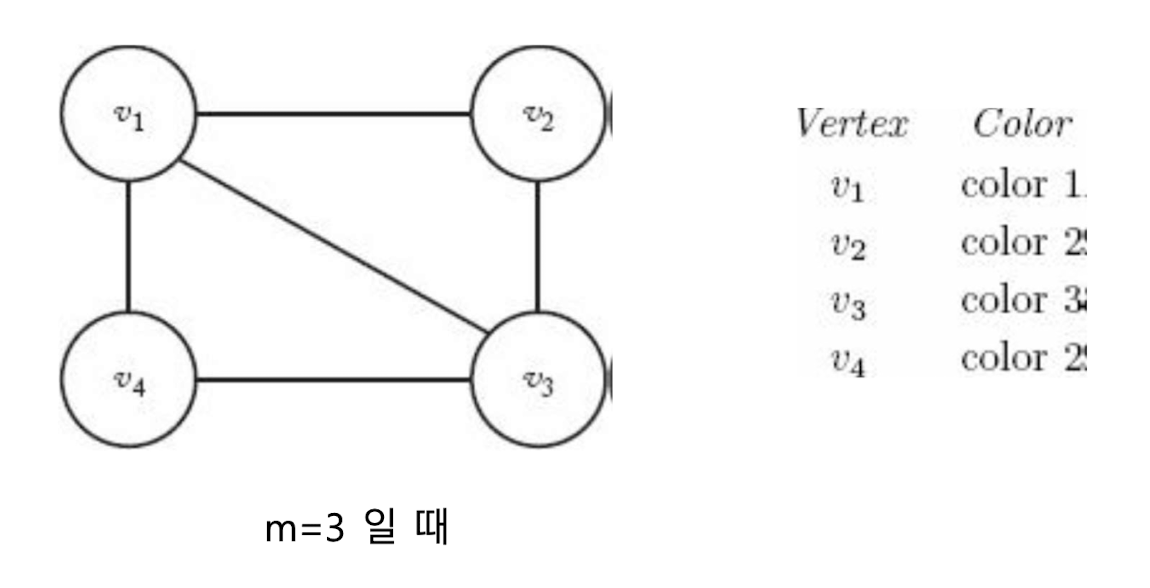
• Graph의 각 Node를 서로 다른 m개의 색을 사용해서 칠하되 인접한 Node는 색이 서로 달라야 함
• m의 값에 따라 달라지는 별개의 문제
• Graph가 주어졌을 때 m = 2이면 Solution이 없는 경우가 많다.

Graph Coloring

• Graph Coloring의 주요 Application 중 하나는 Map Coloring

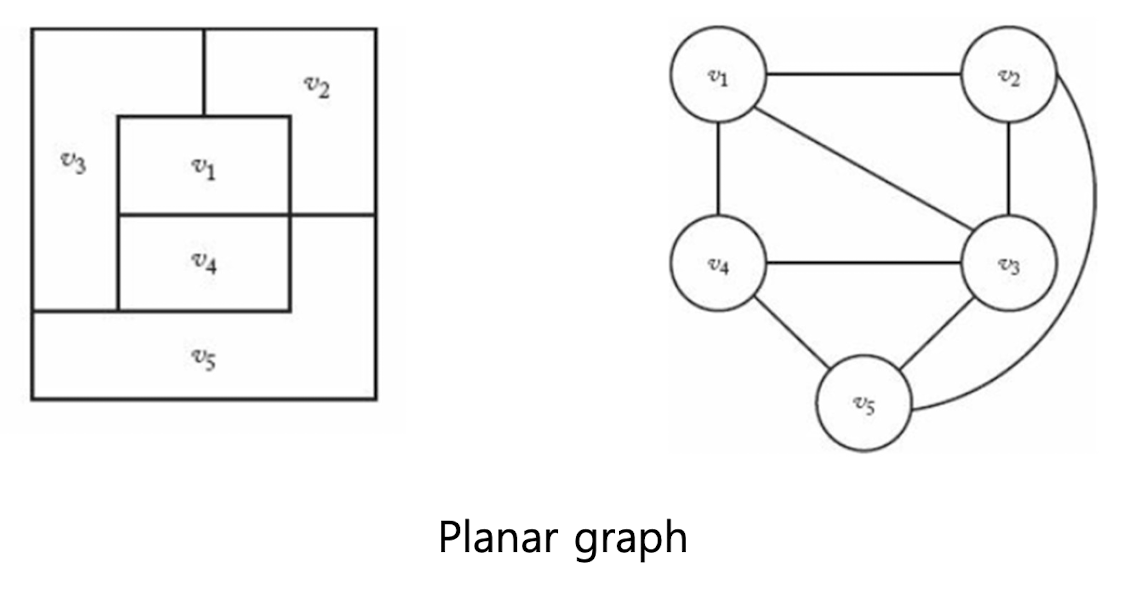
• Planar Graph: Graph에서 Edge가 서로 만나는 것이 없을 때

  • 모든 Map은 Planar Graph로 표현 가능

  • 각각의 Region은 Vertex로 표현, 인접한 Region 간에 Edge 연결

  • m-Coloring은 Planar Graph를 그 대상으로 함

  • Adjacency Matrix로 Edge 표현 (Weight가 없으므로 True/False로 충분)
    

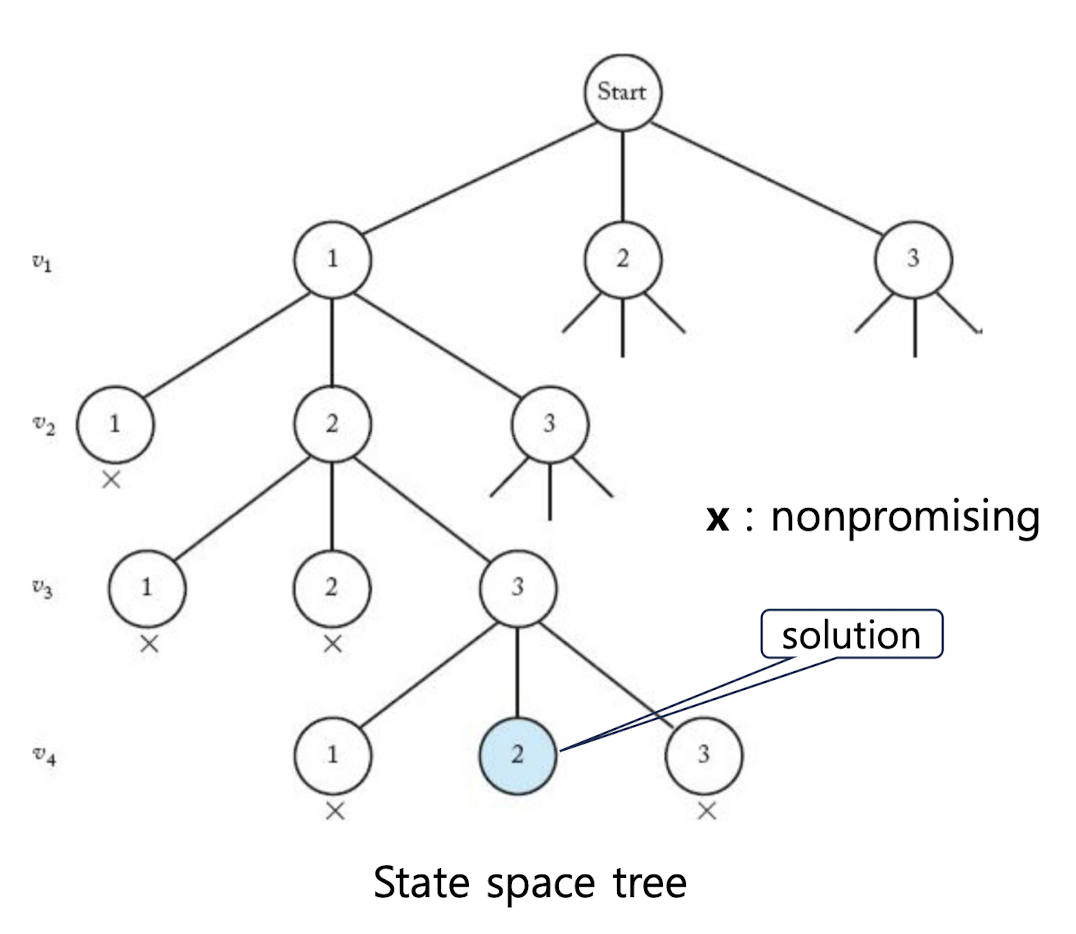
  • State Space Tree
    

m-Coloring Problem

• Problem: Undirected Graph의 모든 Vertex가 m개의 색을 사용하여 인접한 Vertex간 서로 다른 색으로 칠해지는 색의 조합을 찾는 것
  • Inputs: n(Vertex의 개수), m(색의 수), Adjacency Matrix
  • Outputs: 주어진 조건을 만족하는 Node 1 ~ n의 색깔 (vcolor[1..n])
• Worst Case
  • m = 2일 때, vₙ은 모든 Vertex와 Edge가 있고, 다른 Edge는 {vₙ₋₂, vₙ₋₁}이 유일할 때
  • State Space Tree의 Node 개수
    
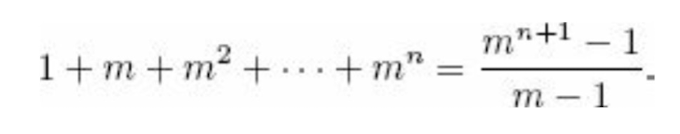
• Other Case
  • m = 5일 때 모든 지도를 칠할 수 있음이 증명되었으나 m = 4인 경우에 대해서는 아무도 증명하지 못함
  • m = 4일 때 모든 지도를 칠할 수 있음이 증명
    • 이론적으로 생성 가능한 모든 지도를 만들고, 컴퓨터를 이용하여 모든 지도에 4색으로 색칠이 가능함을 보임
    • 이론적 증명이 아닌 컴퓨터 Simulation에 의한 최초의 증명
      → 4색 문제: 현재까지 아무도 이론적 증명을 못한 Open Problem으로 존재

Hamiltonian Circuits Problem

• Traveling Salesperson, Dynamic Programming
  • Nancy와 Ralph가 20개의 도시에 대해 경쟁
  • 모든 도시를 경유하는 가장 짧은 경로를 먼저 계산하는 사람이 영업권 획득
  • Nancy는 Dynamic Programming을 사용하여 45초 소요, Ralph는 모든 경우의 수(n!)를 계산하여 3,800년 소요
  • 만약 도시의 개수가 40개가 되면 Nancy도 6.46년 소요
• 도시의 수가 많아지면 최단 경로 계산은 어려워짐
• 경로 중 하나를 찾는 것으로 문제를 바꾸면 → Hamiltonian Circuits
  • 모든 Vertex가 다른 모든 Vertex와 Edge로 연결된 경우
    Traveling Salesperson → Worst Case
    Hamiltonian Circuit → Best Case

Hamiltonian Circuits Problem

• Graph의 한 Vertex를 출발하여 다른 모든 Vertex들을 한 번씩만 경유하여 원래의 Vertex로 돌아오는 문제

• 경로 중 하나만 찾으면 됨
  

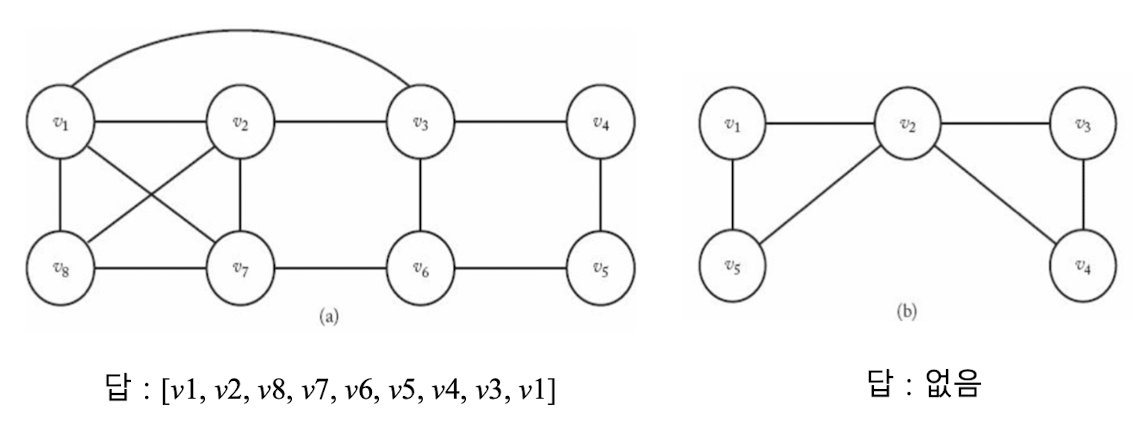
• Problem: Undirected Graph에서 Hamiltonian Circuit 구하기

• Inputs: n(Vertex의 개수), Adjacency Matrix

• Outputs: 임의의 Vertex에서 시작해서 모든 Vertex를 한 번만 경유하고 출발 Vertex로 오는 경로 vindex[0..n-1]

• Promising 조건

  • 경로 상의 i번째 Vertex는 i-1번째 Vertex와 인접해야 한다.

  • n-1번째 Vertex는 0번째 Vertex (출발 Vertex)와 인접해야 한다.

  • i번째 Vertex는 i-1번째 까지의 경로 상에 존재하면 안된다.

  • State Space Tree의 노드 수
    

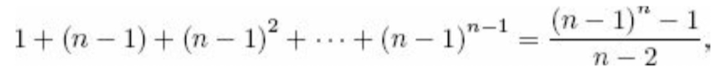
  • Worst Case

    • v₁은 v₂와 연결된 하나의 Edge만 있고 나머지 Vertex들은 Fully Connected 일 때, Solution은 존재하지 않고 최악의 시간복잡도를 가짐

0-1 Knapsack Problem

0-1 Knapsack Problem

• Item들은 각각 Weight와 Profit을 가지고 있음
• Item들의 무게의 합이 W를 넘지 않으면서 Profit이 최고가 되도록 Knapsack에 Item을 담아야 함
• Optimization Problem → 모든 경우의 수를 다 계산하지 않고서는 최적의 값을 보장할 수 없음
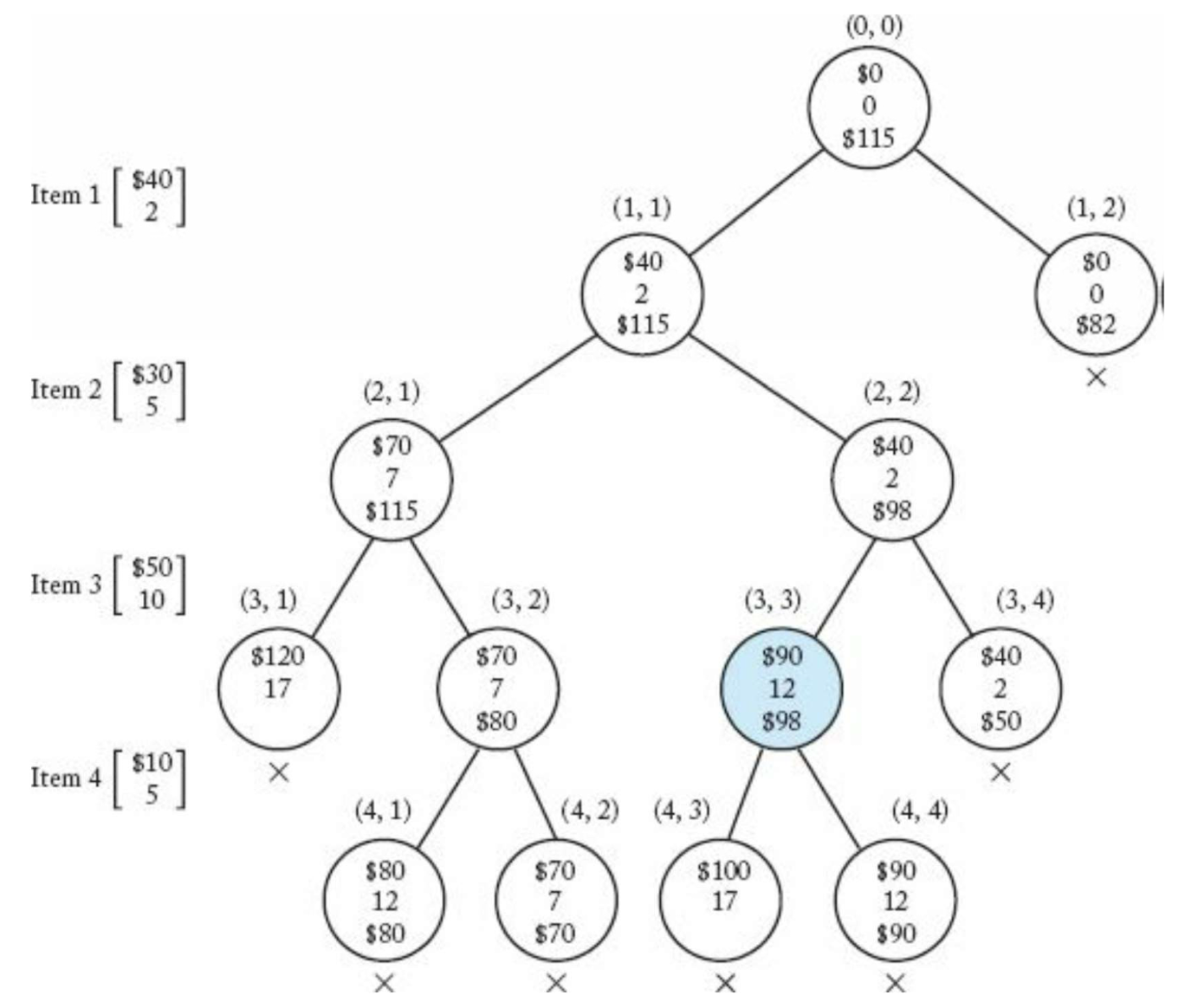
• State Space Tree의 Left Child는 해당 Item을 포함하는 경우를 의미, Right Child는 포함하지 않는 경우를 의미
• Optimization Problem에서 Promising은 Child Node로 확장할 수 있는 Node를 의미
• State Space Tree 상에서 Nonpromising의 조건
  • W ≤ Weight
  • Bound ≤ Max Profit
• State Space Tree의 각 노드는 다음 값을 가짐
  • Profit: 현재 Node까지의 Profit의 합
  • Weight: 현재 Node까지의 Weight의 합
  • Bound: 현재 Node에서 계속 Expand할 경우 얻을 수 있는 최대 Profit