[알고리즘] Leetcode_108_Convert_Sorted_Array_to_Binary_Search_Tree

Problem

Solve

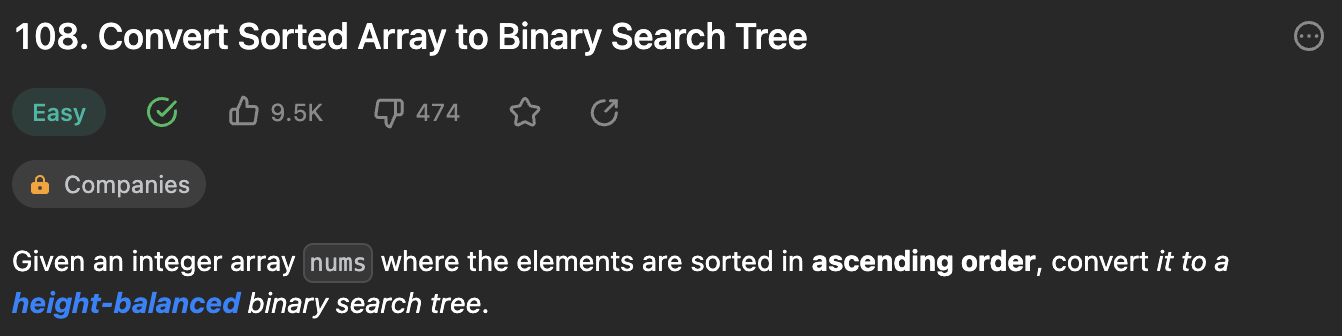
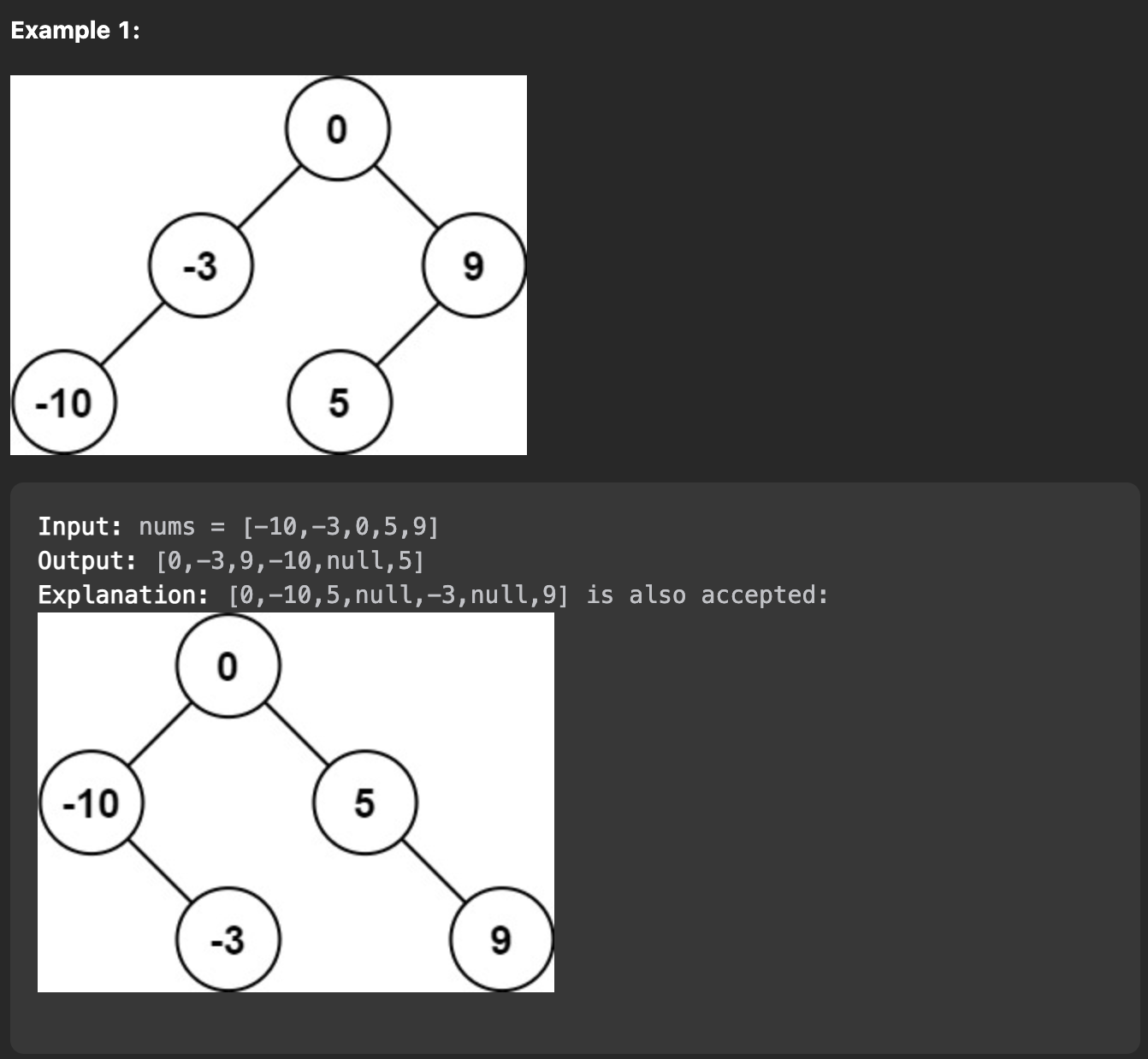
• 이진 탐색 트리 (Binary Search Tree) 는 모든 노드가 key라는 값을 가지고, 각 노드의 왼쪽 서브트리는 현재 그 노드의 값보다 작은 값을 가지고, 오른쪽 서브트리는 큰 값을 가진다. 따라서 재귀로 구현할 수 있어서 탐색하는데 매우 효율적이고 삽입이나 삭제 시 O(log n)의 시간 복잡도를 가진다.
• TreeNode 형으로 반환해야 해서 시작을 어떻게 잡아야하는지 헷갈렸다. 그래서 배열이 오름차순으로 정렬되어 있기 때문에 배열의 첫번째 값을 루트로 정해주었고, 그 이후의 삽입과정을 실시하도록 했다.

public class Leetcode_108_Convert_Sorted_Array_to_Binary_Search_Tree {
    public static TreeNode insertTree(TreeNode current, int num){
        if(current == null) return new TreeNode(num);

        if(num < current.val){
            current.left = insertTree(current.left, num);
        }else if(num > current.val){
            current.right = insertTree(current.right, num);
        }else{
            return current;
        }

        return current;
    }

    public static TreeNode sortedArrayToBST(int[] nums) {
        if (nums == null || nums.length == 0) {
            return null;
        }
        TreeNode answer = new TreeNode(nums[0]);
        for(int i = 1 ; i < nums.length ;i++){
           answer = insertTree(answer, nums[i]);
        }
        return answer;
    }

    public static void main(String[] args){
        int[] nums = { -10, -3, 0, 9, 5};
        TreeNode result = sortedArrayToBST(nums);
    }
}

그치만 루트노드가 첫번째 배열로 고정이 되어 있기 때문에 삽입 과정이 이루어지지 않았다.

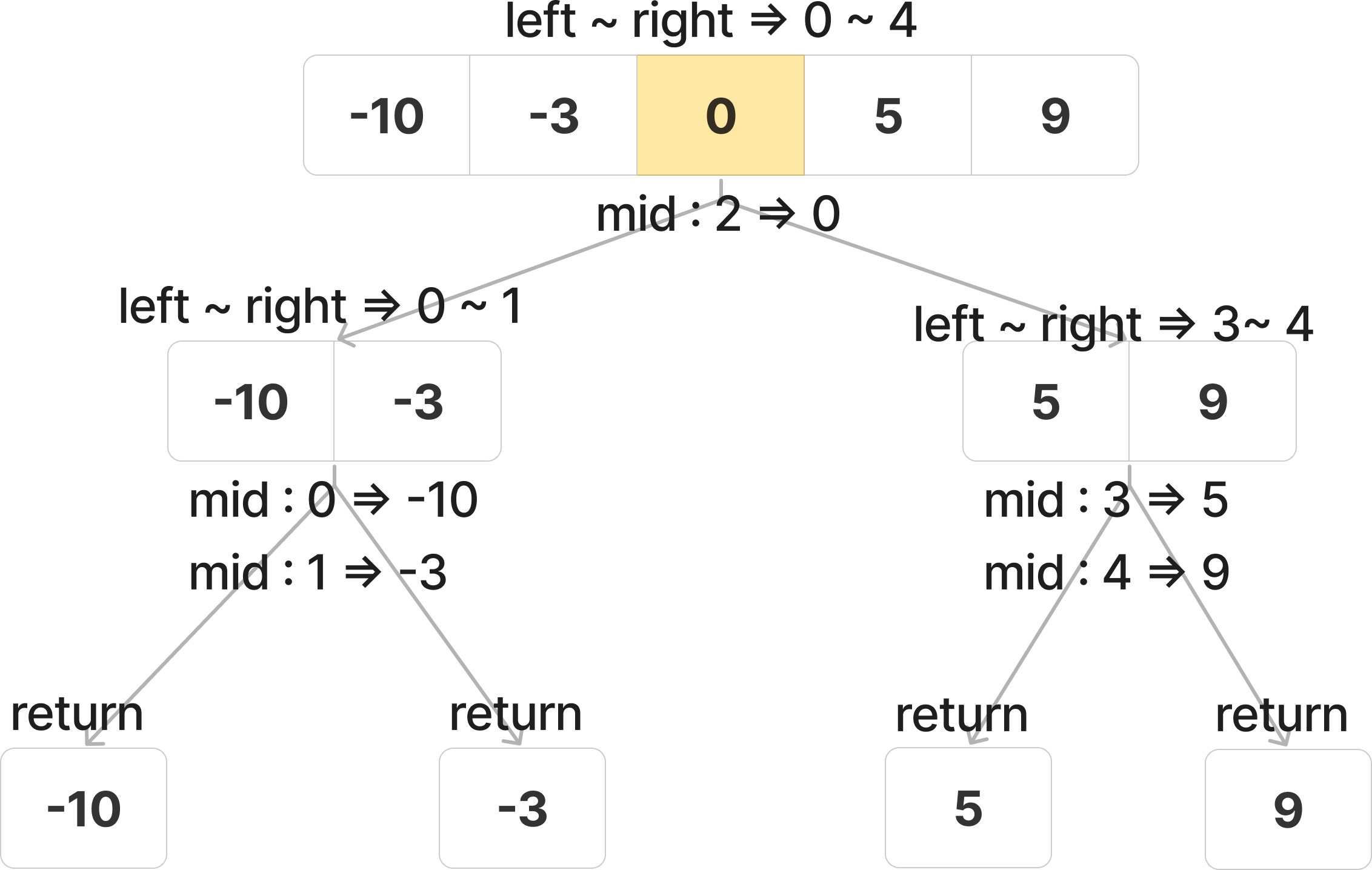
• 그렇다! 앞서 언급한 것처럼 nums 배열은 오름차순으로 정렬이 되어있기 때문에 가운데값이 루트가 될 것이다. 이는 분할 정복 알고리즘을 이용하면 된다. mid를 중간 지점을 정해주고 왼쪽, 오른쪽의 서브 트리를 생성하기 위해 이 때 재귀 과정을 거치게 된다.
• 왼쪽 서브트리는 nums[mid] 보다 작은 값으로, 오른쪽 서브트리는 nums[mid]보다 큰 값으로 이루어져야 한다.

class Solution {
    public TreeNode insertTree(int[] nums, int left, int right){
        if(left > right) return null;

        int mid = (left + right) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = insertTree(nums, left, mid-1);
        root.right = insertTree(nums, mid+1, right);

        return root;

    }
    public TreeNode sortedArrayToBST(int[] nums) {
        return insertTree(nums, 0, nums.length-1);
    }
}

분할 정복 Divide and Conquer

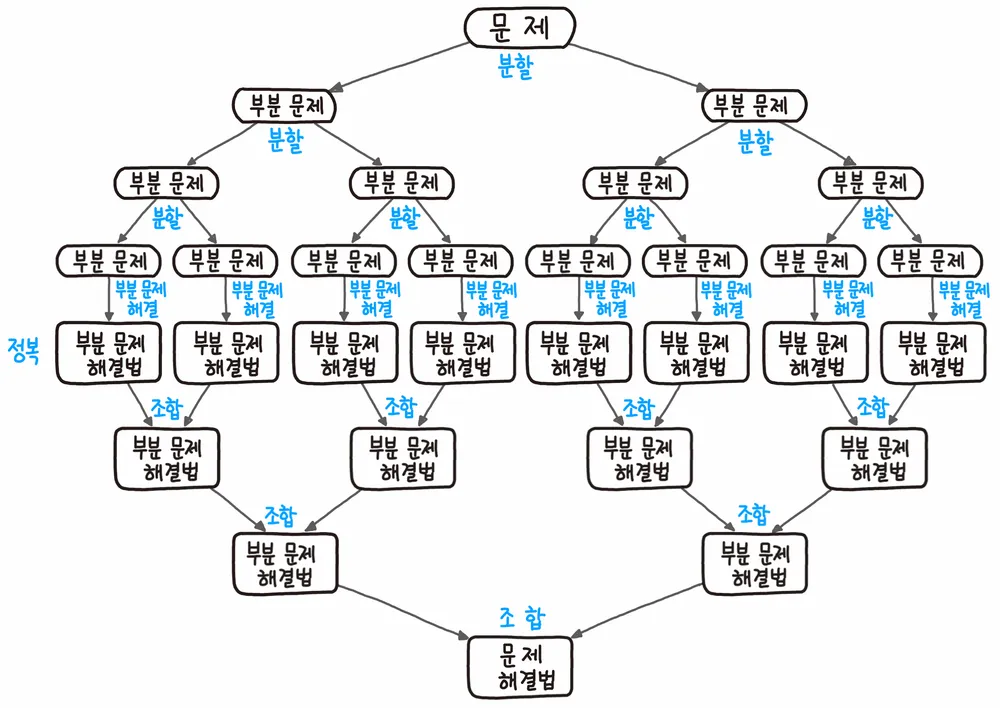
분할 정복(Divide and Conquer) 알고리즘은 대개 재귀적으로 구현되며, 다음과 같은 세 가지 단계로 이루어져 있다.

• 분할(Divide): 주어진 문제를 작은 부분 문제로 분할
• 정복(Conquer): 작은 부분 문제들을 각각 해결한다. 부분 문제가 충분히 작다면, 순환적으로(base case) 해결된다.
• 합병(Combine): 작은 부분 문제들의 해결책을 합병해 전체 문제의 해답을 구합니다.
  이러한 과정은 하향식(Top-Down)으로 수행되며, 문제를 해결하기 위해 동일한 알고리즘을 다시 호출해야 한다.

분할 정복 알고리즘의 시간 복잡도는 분할된 각각의 부분 문제들의 크기에 따라 결정되는데, 일반적으로 문제를 반씩 분할하므로 분할된 부분 문제들의 크기는 절반으로 감소한다.
따라서 분할된 부분 문제들의 수는 log n이 된다. 각 부분 문제들의 해결에 걸리는 시간은 일반적으로 상수 시간 또는 선형 시간이므로, 분할 정복 알고리즘의 시간 복잡도는 O(n log n)이다.