[알고리즘] Leetcode_310_Minimum_Height_Trees

jeongjwon·2023년 4월 28일

알고리즘

목록 보기

43/48

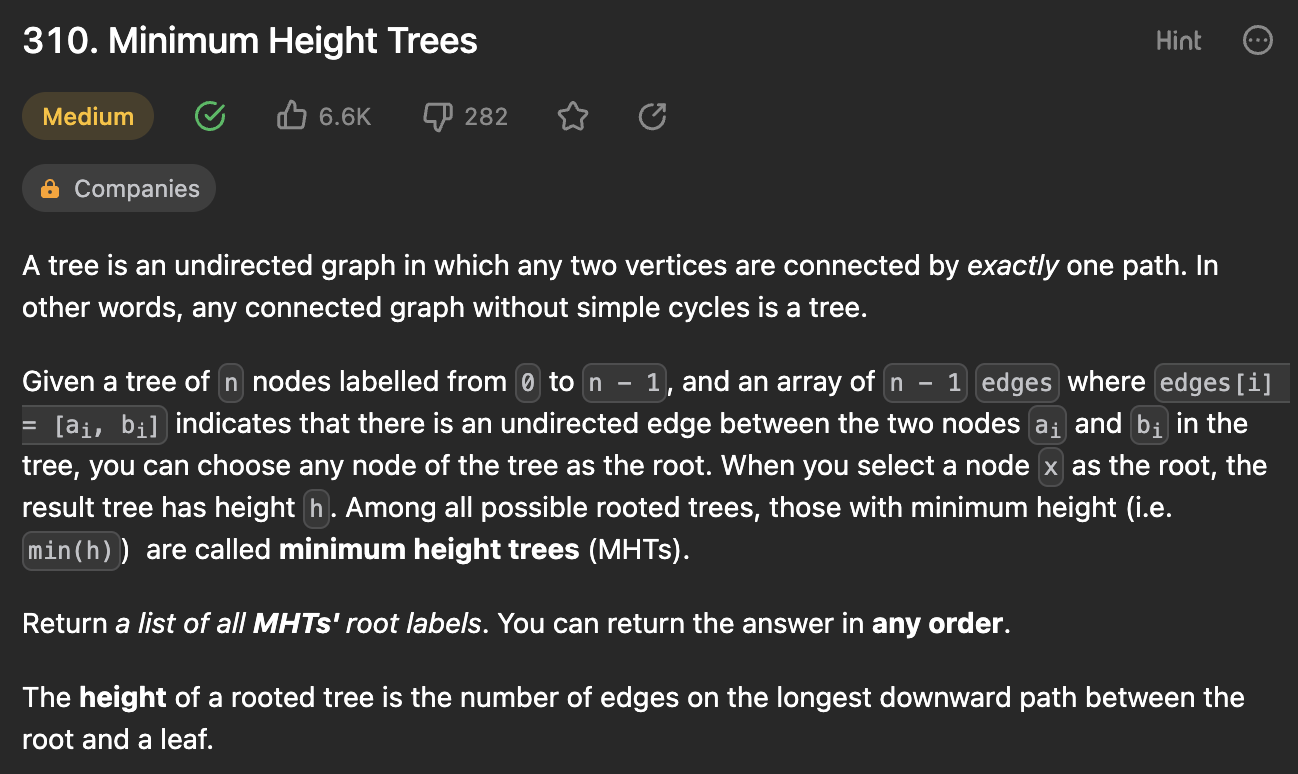
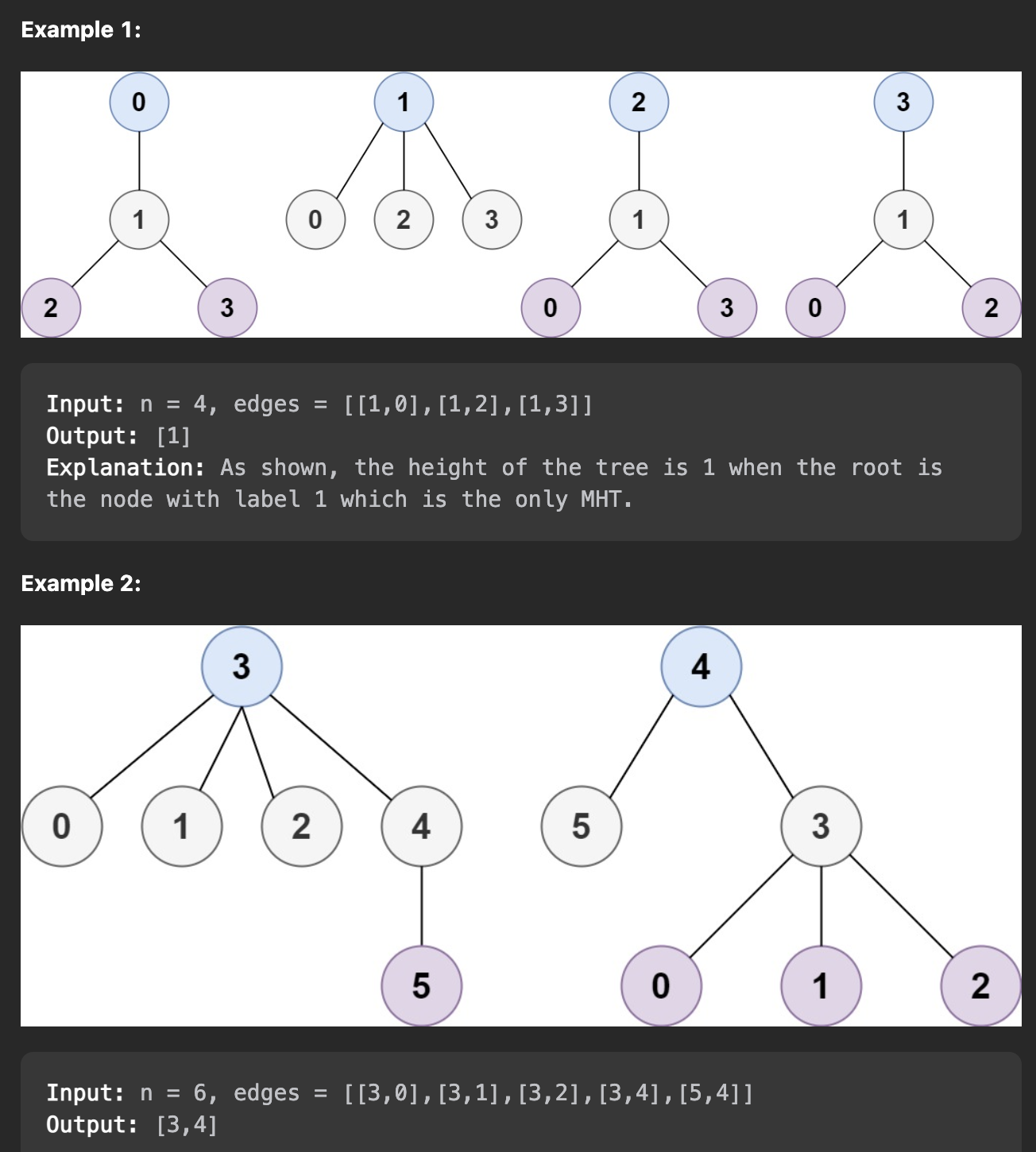
Problem

Solve

MST 알고리즘이지만 가중치가 존재하지 않는 무방향 그래프
높이가 최소인 트리가 되려면 가장 연결이 많은 노드가 루트가 되어야 한다.
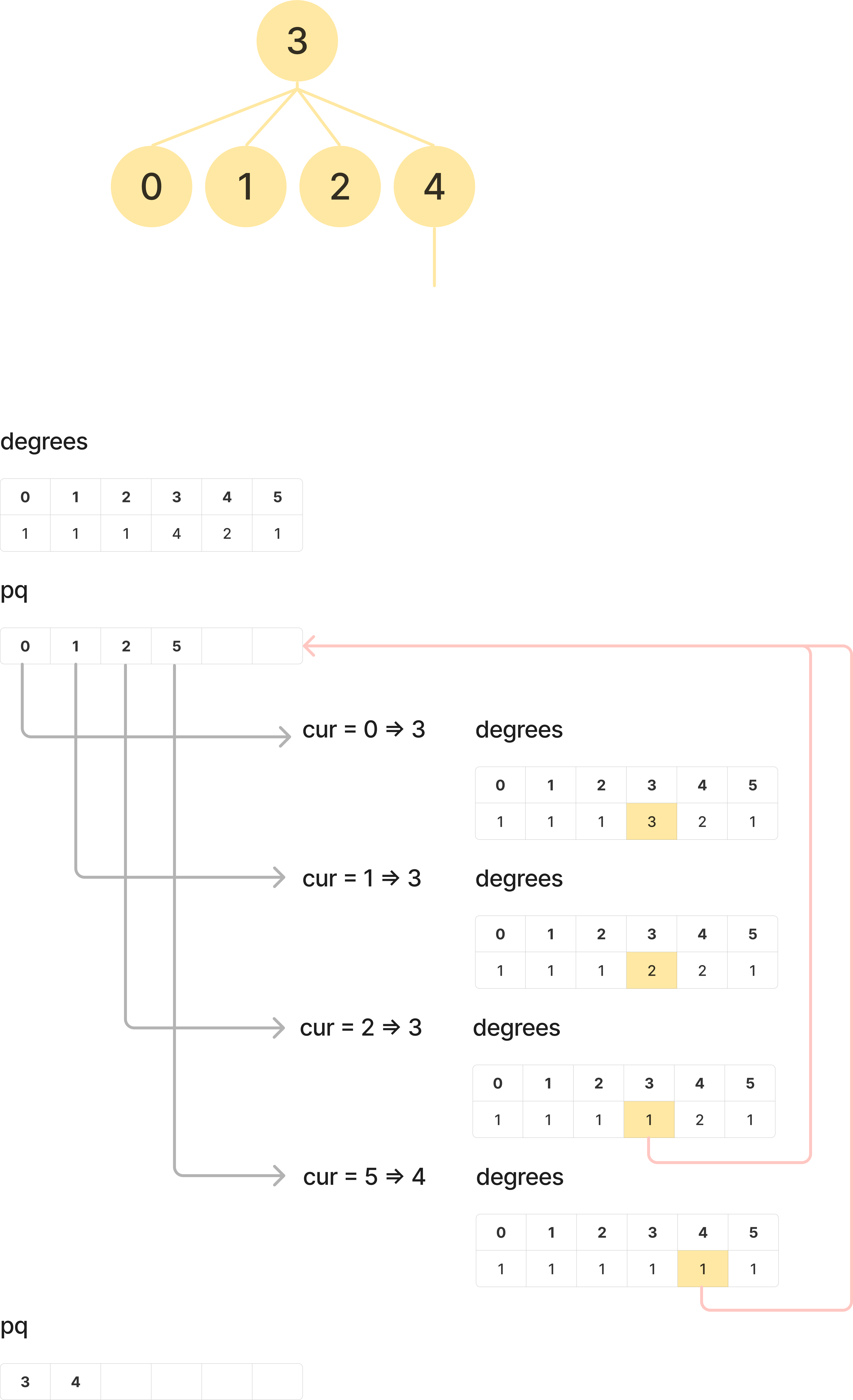
위에서 언급한 트리의 특성을 이용하여 차수(=간선의 개수) 배열을 생성한다.
리프노드 (=차수가 1인 노드) 를 큐에 삽입하고 트리의 높이가 1이거나 2인 경우를 위해 while문 조건을 n > 2 을 설정하고 매 단계마다 리프노드를 제거하면서 그래프의 크기를 줄여나간다.
마지막에는 결국 루트 노드를 제외한 모든 노드가 리프 노드가 루프노드가 됨

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {

        if(n == 1){
            List<Integer> answer = new ArrayList<>();
             answer.add(0);
             return answer;
        }

        List<List<Integer>> graph = new ArrayList<>();
        for(int i = 0 ; i < n ; i++) graph.add(new ArrayList<>());

        int[] degrees = new int[n];

        for(int[] edge : edges){
            int u = edge[0];
            int v = edge[1];
            graph.get(u).add(v);
            graph.get(v).add(u);
            //무방향 그래프이기 때문에 간선을 두 개 연결해줌

            degrees[u]++;
            degrees[v]++;
            //간선의 개수 = 차수 
        }
       Queue<Integer> queue = new LinkedList<>();


        for(int i = 0 ; i < n ; i++){
            if(degrees[i] == 1) queue.offer(i);
            //간선이 하나 == 리프노드
        }

        while(n > 2){
            int size = queue.size();
            n -= size;
            for(int i = 0 ; i < size ; i++){
                 int cur = queue.poll();
                for(int next : graph.get(cur)){
                    degrees[next]--;
                //차수 감소
                    if(degrees[next]==1) queue.offer(next);
                }
            }
           
        }

        List<Integer> answer = new ArrayList<>(queue);
        return answer;
    }
}