차원 축소의 필요성
고차원 데이터
- 데이터의 피처(변수)가 매우 많은 상태를 말합니다. 예컨대 이미지 데이터의 경우, 한 장의 이미
지를 구성하는 픽셀 수만큼의 피처가 있을 수 있습니다.
문제들
- 모델 학습 시 연산 복잡도가 급증하여 시간이 오래 걸림
- 많은 피처들 중 일부는 실제로 중요한 정보를 주지 못하는 노이즈(잡음)일 수 있음
- 차원이 너무 높아지면 데이터를 시각화하기가 어려워 패턴 파악이 힘듬
차원 축소의 장점
- 노이즈 제거로 모델 성능 및 일반화 능력을 개선할 수 있음
- 2차원이나 3차원으로 축소하면 시각적으로 직관적인 분석을 할 수 있음
- 데이터의 핵심 구조나 패턴을 더 쉽게 발견할 수 있음
선형 차원 축소
- 특정 선형 변환으로 투영하여 차원을 줄이는 기법. PCA가 대표적
비선형 차원축소
- 데이터가 복잡한 기하학적 구조를 가질 때, 선형 변환만으로는 충분치 않을 수 있으므로
비선형 맵핑을 이용. t-SNE, UMAP등이 해당
PCA(주성분 분석)
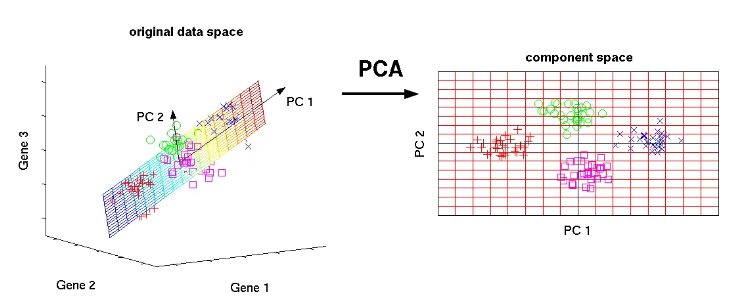
- 데이터에서 가장 분산이 큰 방향(주성분)을 찾아 그 방향으로 데이터를 투영하면, 그 축이 데이
터의 중요한 변동을 많이 설명
주성분
- 가장 큰 분산을 갖는 방향을 1주성분으로, 그다음으로는 큰 분산을 갖는 서로 직교(90도)하는
방향을 2주성분으로 하는 식으로 이어진다
설명 분산 비율
- 몇 개의 주성분만으로 전체 분산의 몇 퍼센트를 설명할 수 있는지 나타낸다.
PCA의 장단점
-
장점 : 계산이 비교적 간단, 결과 해석이 용이, 노이즈 제거 효과
-
단점 : 데이터가 선형이 아닌 패턴일 경우 정보 손실이 발생할 수 있음, 매우 복잡한 구조를
충분히 반영이 어려움
t-SNE, UMAP
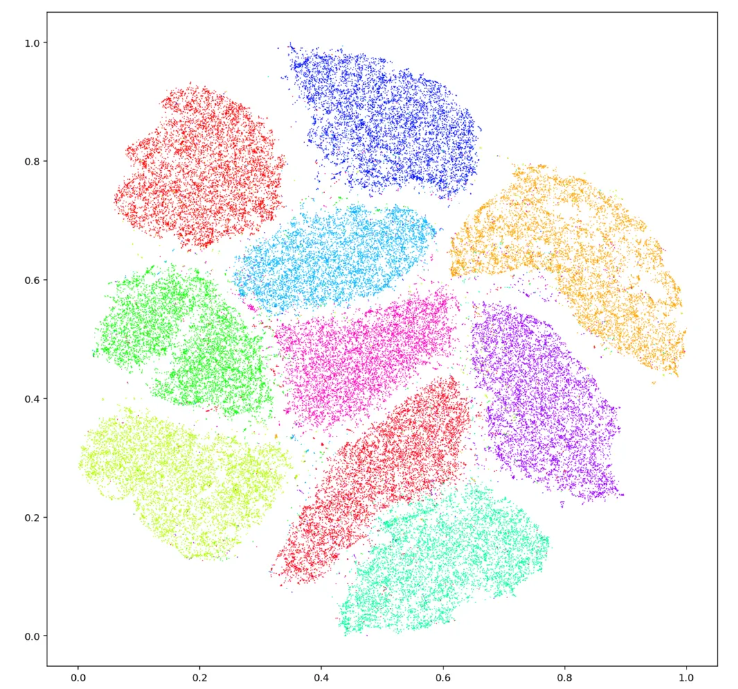
t-SNE
- 고차원 공간에서 서로 가까운 데이터 포인트는 가까이, 먼 데이터 포인트는 멀리 배치하려고 하
는 비선형 차원 축소 기법
동작 원리
- 고차원에서 데이터 간 지역적 확률 분포를 추정
- 2차원 혹은 3차원에서 비슷한 확률 분포가 되도록 데이터들을 배치
장점
- 데이터의 군집이 자연스럽게 시곽화되어, 군집별 패턴을 인지하기 쉬움
단점
- 계산 비용이 큼
- 하이퍼파라미터 선택에 따라 결과가 달라질 수 있음
- 시각화 결과 해석이 직관적이지만, 실제 거리 척도가 왜곡될 수 있음
UMAP
- t-SNE와 유사하게 고차원 데이터 구조를 2D/3D로 매핑하는 비선형 차원 축소 기법
장점
- t-SNE보다 빠르고, 대규모 데이터에 비교적 효율적
- 지역적/글로벌 구조를 함께 잘 반영
단점
- 알고리즘의 개념이 비교적 복잡하고, 하이퍼파라미터 튜닝을 요한다
- t-SNE만큼은 아니지만, 여전히 축소 과정에서 정보 왜곡이 발생할 수 있음
