학습 목표

---

후기

---

학습 내용

27. Likelihood(MLE와 MAP)

27.1 들어가며: 머신러닝의 목표

모델이 표현하는 확률 분포를 데이터의 실제 분포에 가깝게 만드는 최적의 파라미터 값을 찾는 것

27.2 posterior와 prior, likelihood 사이의 관계

(1) 사전 확률, 가능도, 사후 확률(prior, likelihood, posterior)

• 사전 확률(prior)
  • 데이터를 관찰하기 전 파라미터 공간에 주어진 확률 분포 $p(\mathbf{\theta})$

• 가능도(likelihood, 우도)
  • 만약 prior 분포를 고정시킨다면, 주어진 파라미터 분포에 대해서 우리가 갖고 있는 데이터가 얼마나 '그럴듯한지' 나타내는 값 $p(X=x∣θ)$
  • 즉, 파라미터의 분포 $p(\mathbf{\theta})$가 정해졌을 때 $x$라는 데이터가 관찰될 확률
  • $L(θ∣x)$로 표현하기도 함

• 최대 가능도 추정(maximum likelihood estimation, MLE)
  • 데이터들의 likelihood 값을 최대화하는 방향으로 모델을 학습시키는 방법

• posterior(posterior probability, 사후 확률)
  • 데이터 집합 XX가 주어졌을 때 파라미터 $\mathbf{\theta}$의 분포 $p(\mathbf{\theta}|X)$
  • 즉, 데이터를 관찰한 후 계산되는 확률

• 최대 사후 확률 추정(maximum a posteriori estimation, MAP)
  • posterior를 최대화하는 방향으로 모델을 학습시키는 방법

(2) posterior와 prior, likelihood 사이의 관계

$p(X,θ)=p(θ∣X)p(X)=p(X∣θ)p(θ)$

양변을 $p(X)$로 나누어주면 베이즈 정리와 같은 식

$p(θ∣X)=\frac{p(X)p(X∣θ)}{p(θ)}$

$\left(\textrm{posterior}=\frac{\textrm{likelihood} \times \textrm{prior}}{\textrm{evidence}},\textrm{posterior}\propto\textrm{likelihood} \times \textrm{prior}\right)$

27.3 likelihood와 머신러닝

파라미터 분포 $\mathbf{\theta}$와 입력 데이터 $\mathbf{x}_n$이 주어졌을 때 라벨 $y_n$을 예측하는 문제

27.4 likelihood 감 잡기

• 데이터 포인트가 모델 함수에서 멀어질수록 데이터의 likelihood는 기하급수적으로 감소
• 예측값과 라벨의 차이가 조금만 벌어져도 likelihood 값은 민감하게 반응
• 머신러닝의 목표는 데이터 포인트들의 likelihood 값을 크게 하는 모델을 찾는 것

27.5 MLE: 최대 가능도 추론

데이터의 likelihood 값을 최대화하는 모델 파라미터를 찾는 방법

(1) 데이터셋 전체의 likelihood

모델 파라미터 $θ$가 주어졌을 때, 데이터 포인트 $(\mathbf{x}_n, y_n)$의 likelihood는 다음과 같습니다.

$p(y_n∣θ,x_n)=N(y_n∣θ^⊤x_n,σ^2)=\frac{1}{\sqrt{2πσ^2}}exp(−\frac{(y_n−θ^⊤x_n)}{2σ^2})$

데이터 포인트들이 서로 독립이므로, 데이터셋 전체의 likelihood $p(Y|\mathbf{\theta}, X)$는 데이터 포인트 각각의 likelihood를 모두 곱한 값과 같습니다.

$p(Y∣θ,X)=∏_np(y_n∣θ,x_n)$

MLE를 실제로 적용할 때는 likelihood 대신 log likelihood를 최대화하는 파라미터를 구합니다. 데이터셋의 likelihood가 데이터 포인트 각각의 likelihood를 곱한 형태인데, 로그를 씌우면 곱셈 연산이 덧셈 연산으로 바뀌면서 미분 계산이 편리해집니다.
또한 로그 함수는 단조 증가(monotonically increasing)하므로 likelihood를 최대화하는 파라미터와 log likelihood를 최대화하는 파라미터 값이 같아서 학습 결과에 영향을 주지 않습니다.

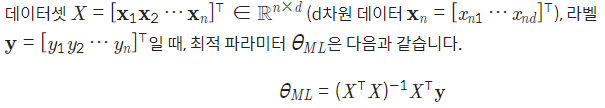
# MLE의 최적해는 오로지 관측된 데이터 값에만 의존 한다

• 계산이 비교적 간단하다는 장점이 있지만, 관측된 데이터에 노이즈가 많이 섞여 있는 경우, 이상치(outlier) 데이터가 존재하는 경우에는 모델의 안정성이 떨어진다는 단점도 있습니다.

27.6 MAP: 최대 사후 확률 추정

prior 분포의 등장

• 직관적으로, 이런 데이터가 있을 때 파라미터의 값이 무엇일 확률이 제일 높은가?

• 데이터셋이 주어졌을 때 파라미터의 분포, 즉 $p(\mathbf{\theta}|X)$에서 확률 값을 최대화하는 파라미터 $\mathbf{\theta}$를 찾습니다.

• MAP의 최적 파라미터
  $θ_{MAP}=(X^⊤X+\frac{σ^2}{α^2}I)^{−1}X^⊤y$

27.7 MLE와 MAP의 비교

MLE와 MAP의 최적 파라미터는 각각 다음과 같습니다.

$\mathbf{\theta}_{MLE} = (X^\top X)^{-1}X^\top\mathbf{y}$
$\mathbf{\theta}_{MAP}=\left(X^\top X+\frac{\sigma^2} {\alpha^2}\mathbf{I}\right)^{-1}X^\top\mathbf{y}$

노이즈 분포의 표준편차 $\sigma$는 0.1로 가정하고, 파라미터 분포의 표준편차 $\alpha$는 0.04로 지정하겠습니다. 정규화 상수 $\lambda$가 $\alpha^2$ 에 반비례하는 값입니다. $\alpha$가 작을수록, 즉 파라미터 분포의 표준편차를 작게 잡을수록 파라미터 값에 대한 제약 조건을 강하게 걸어주는 것과 같습니다.
정규화 측면에서 봐도 $\lambda$ 값이 클수록 모델의 유연성은 감소하죠.