백준 11659, 11660 : 구간 합 구하기

11659 : 구간 합 구하기 4

https://www.acmicpc.net/problem/11659

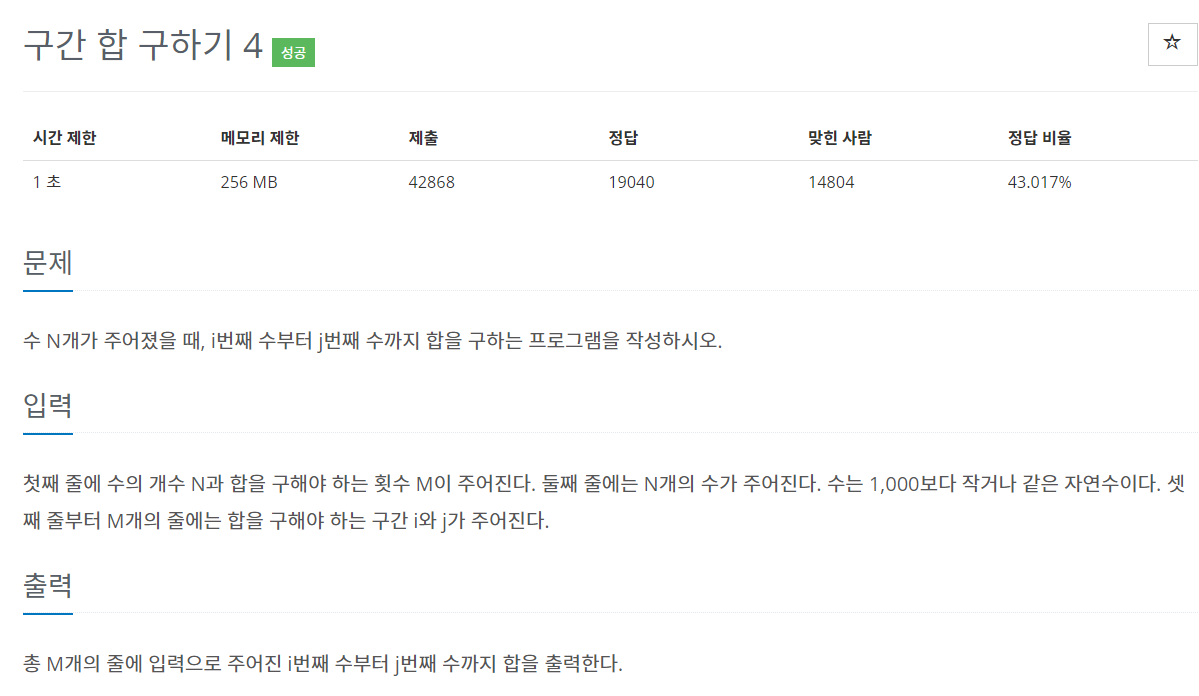
1. 접근

• 처음보면 단순히 For 문으로 덧셈을 진행하면 되는 것처럼 보이지만, 그 경우 2중 For문이 됨

for (int i = 0; i < m; i++) { //m번 정답을 구해야 함
		int from, to;
		cin >> from >> to;
		int answer=0;
        for(int j=from;j<=to;j++) { // 그 때마다 직접 배열에 접근하여 구해줌
        	answer+=arr[j];
        }
		cout << answer << "\n";
	}

=> 이 경우의 시간 복잡도 O(n^2) , 최대 n = 100000
=> 100,000,000 = 1초 정도로 추정
=> 시간 제한 1초 안에 수행이 어려움
=> for문 하나여야 함

• 따라서 DP를 사용해서, 배열 값을 입력함과 동시에 합 값을 구해서 이후 반복적인 값들을 바로 재사용하도록 함
  => For 문이 하나이므로 O(n)

• 합의 최댓값 : 1000 * 100000 = 100,000,000
  => vector 내부의 값은 int로 써도 무방

• 메모리 최댓값 : 4 * 100000

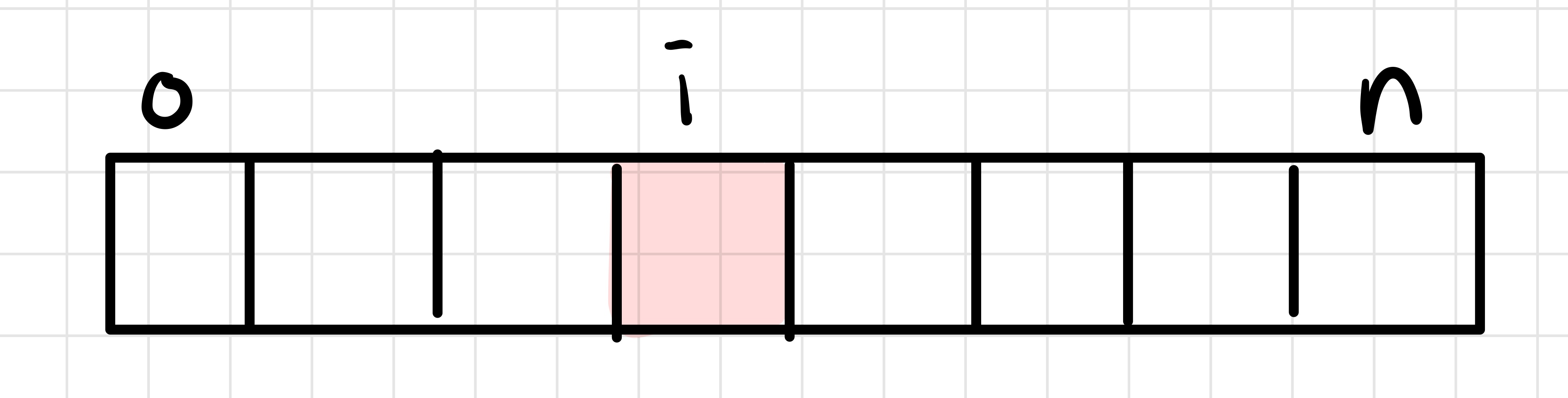
• v[i] : 1번째 원소부터 배열의 i번째 원소까지의 합
• i번째 수행
  1) 0~(i-1) 의 값을 받아옴
  2) 그 값에 현재 값을 더해 v[i]에 저장
  

2. 나의 풀이

#include <iostream>
#include <vector>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n, m;
	cin >> n >> m;
	vector<int> v(n + 1);
	v[0] = 0;

	for (int i = 1; i <= n; i++) {
		int input = 0;
		cin >> input;
		v[i]=v[i-1]+input; //
	}

	for (int i = 0; i < m; i++) {
		int from, to;
		cin >> from >> to;

		cout << (v[to] - v[from - 1]) << "\n";
	}
	return 0;
}

---

11660 : 구간 합 구하기 5

https://www.acmicpc.net/problem/11660

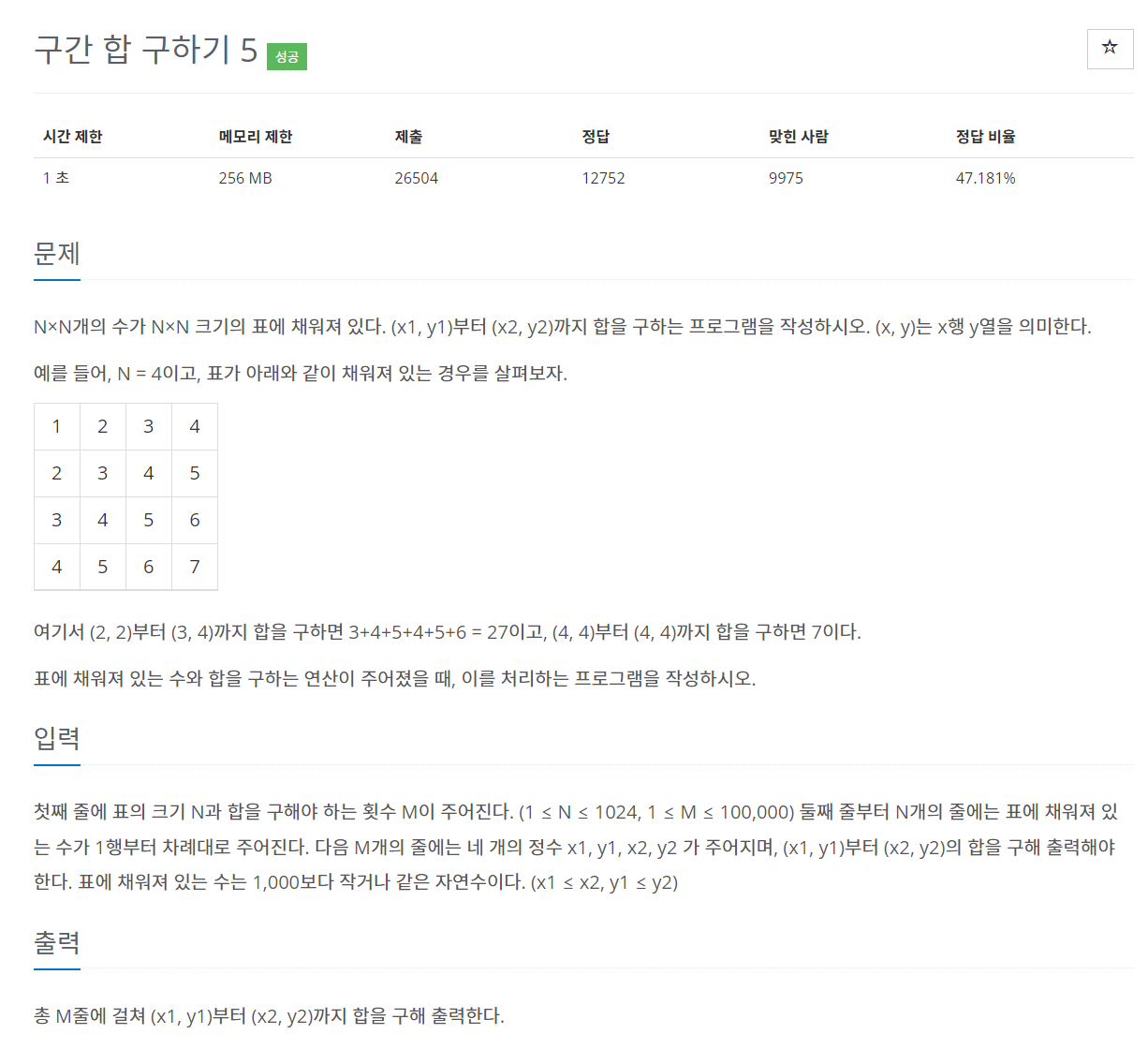
1. 접근

• 기본 접근 방식은 1차원 배열의 위의 문제와 동일

• v[i][j] : (i,j) 원소까지의 누적합
  => 누적합 자체를 어떻게 계산할지가 문제임

• v[i][j]의 값을 구하는 과정을 이해하기
  

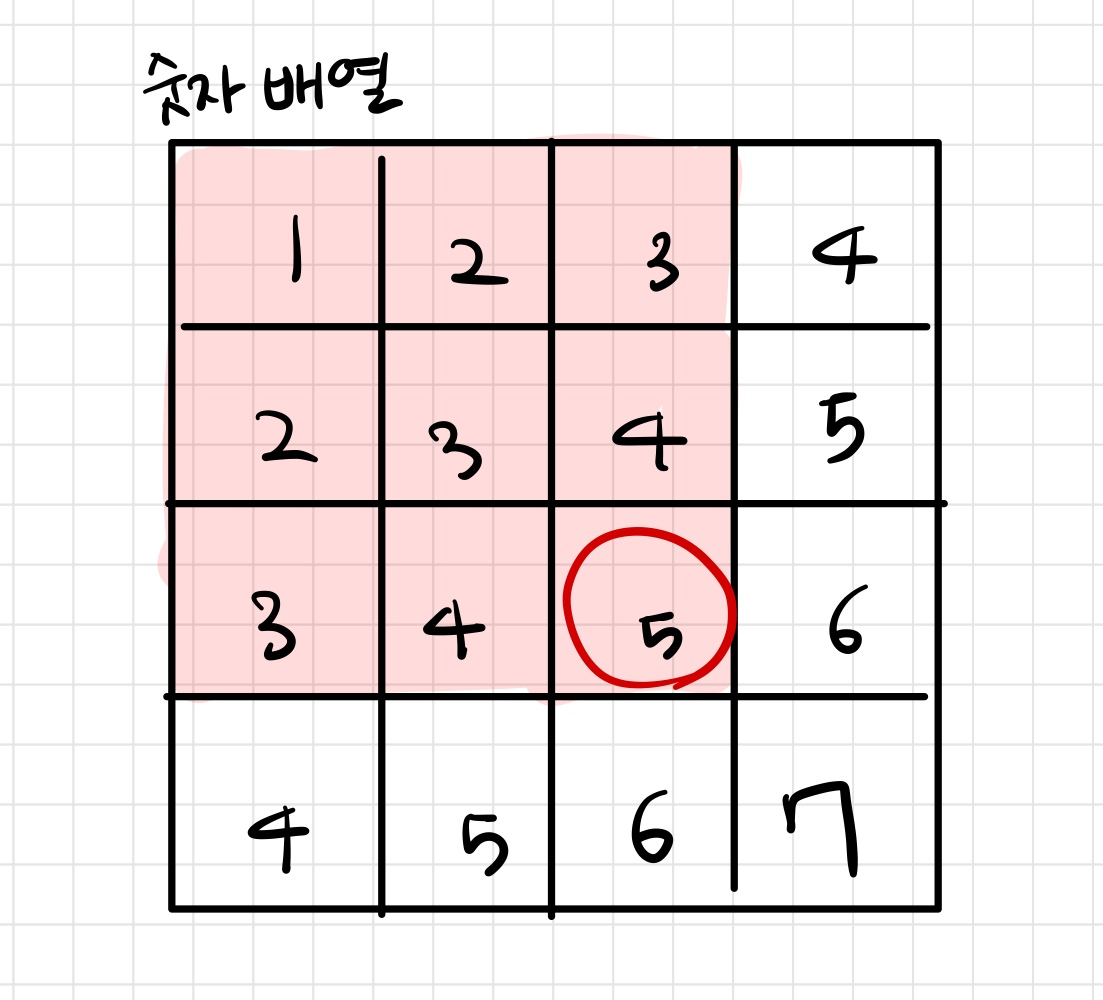
위에서 (3,3) 위치의 5 원소까지의 누적합은 어떻게 구할 수 있을까?

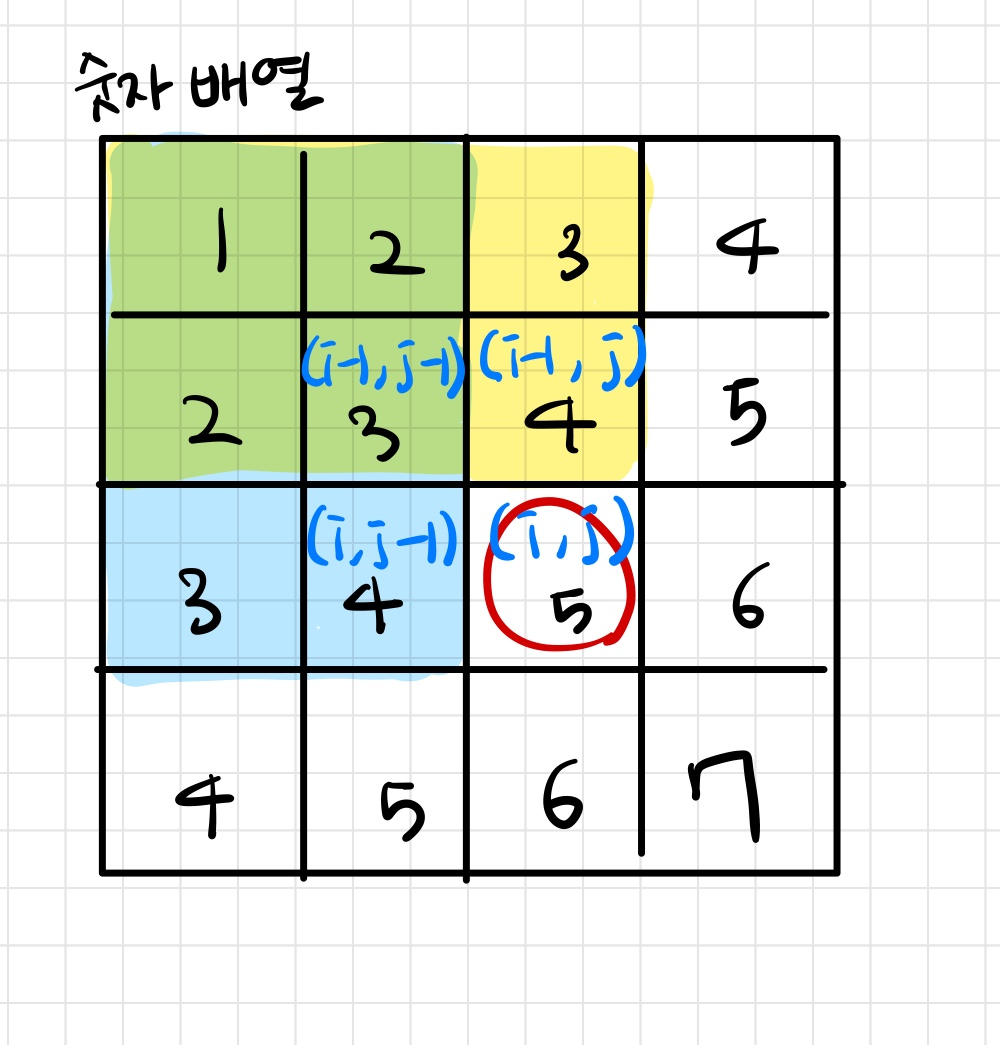
정해진 직사각형들로 사각형의 넓이를 구한다고 생각하면 좋다
(i,j-1)까지의 누적합 직사각형(파랑) 과 (i-1,j) 까지의 누적합(노랑), 그리고 5를 더해주면 된다
여기서 주의할 점은 (i-1,j-1) 까지의 누적합(초록) 부분이 두번 더해진다는 것이다. 그 부분을 마지막에 빼줘야 한다

v[i][j] = v[i - 1][j] + v[i][j - 1]-v[i-1][j-1]+ input;

그럼 위의 이 식이 나온다
이 값을 v 배열에 넣어주면 된다

• (x1,y1) (x2,y2) 사이의 누적합 구하는 과정

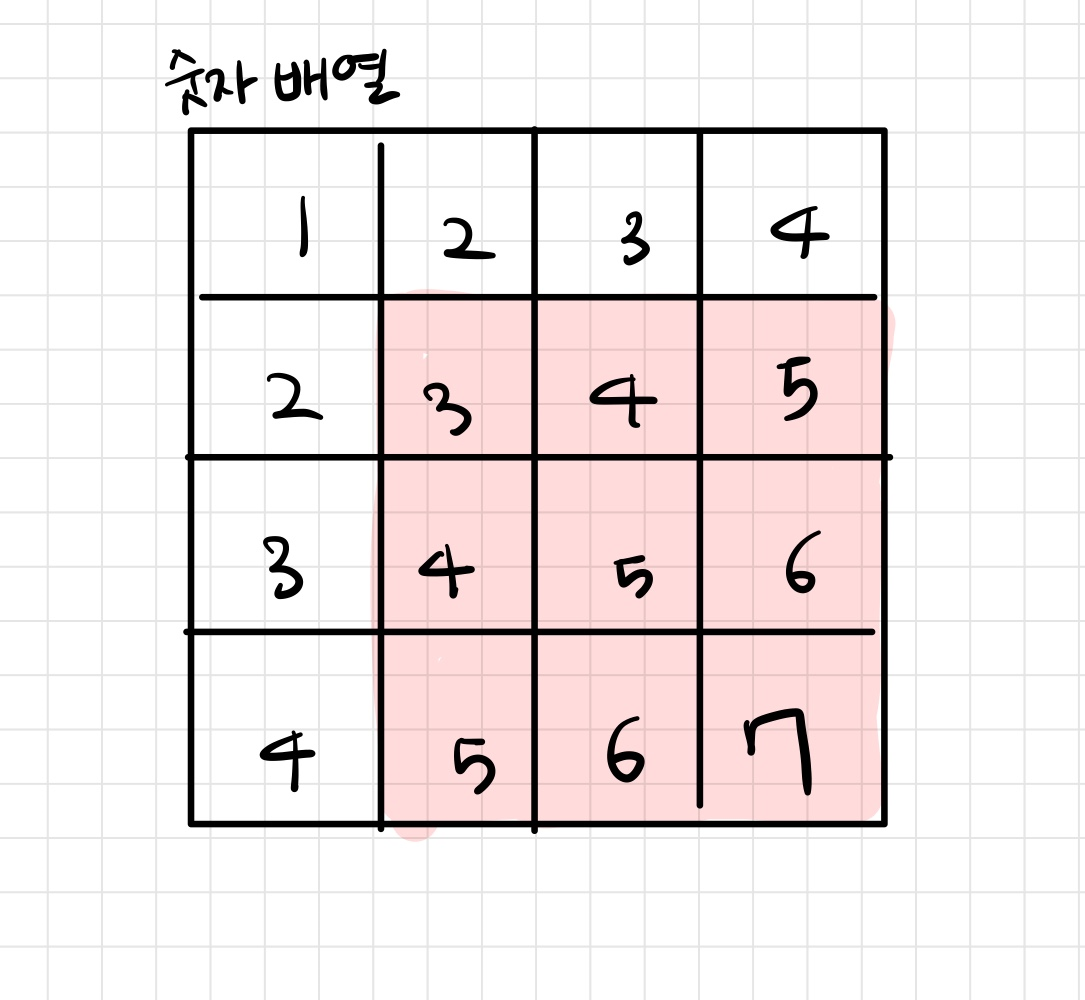
위의 기본 원리와 동일하다.
(2,2) 부터 (4,4) 까지의 합을 구하는 경우

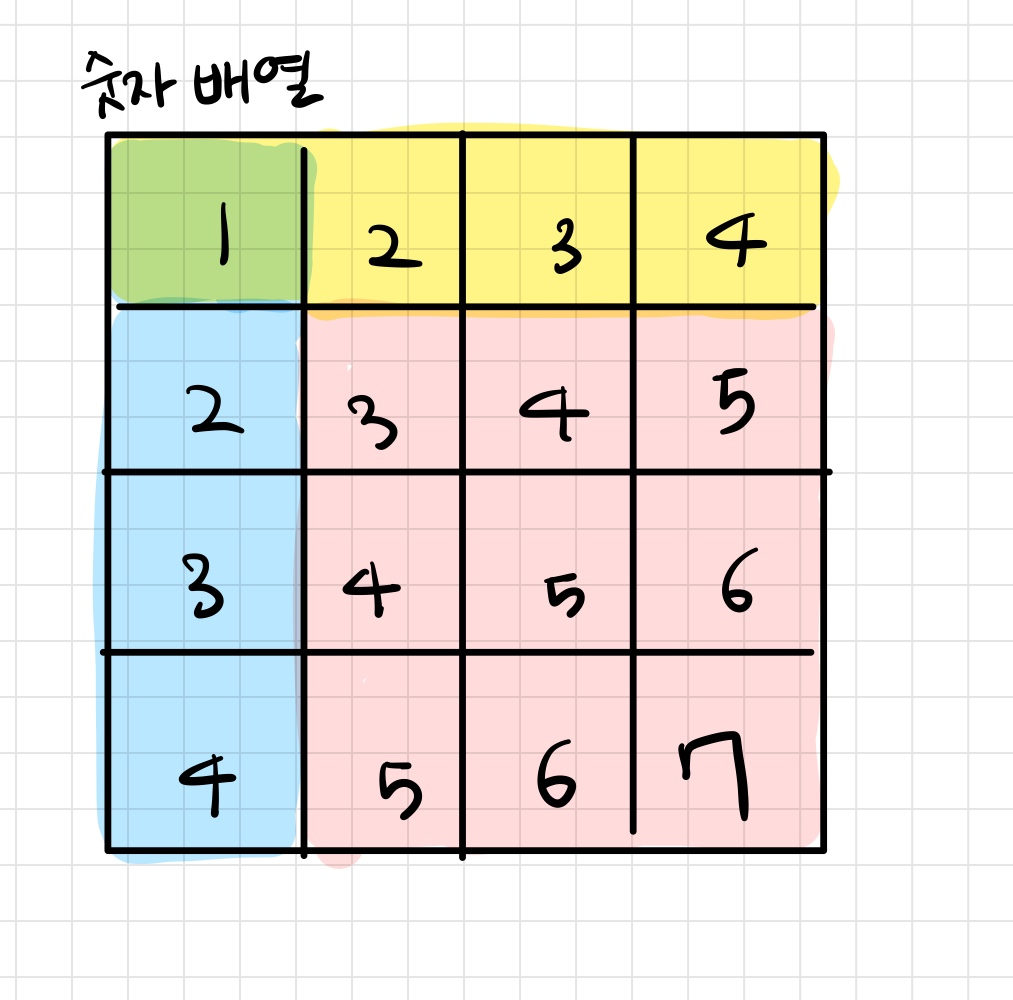
분홍+파랑+노랑-초록 을 해주면 되는 것이다

v[toX][toY] - v[toX][fromY-1] - v[fromX-1][toY] + v[fromX-1][fromY-1]

이것을 그냥 코드로 구현해주기만 하면 된다

2. 나의 풀이

#include <iostream>
#include <vector>
using namespace std;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n, m;
	cin >> n >> m;

	vector<vector<int>> v(n+1);
	for (int i = 0; i <= n; i++) {
		v[i].resize(n+1);
	}

	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			int input;
			cin >> input;
			v[i][j] = v[i - 1][j] + v[i][j - 1]-v[i-1][j-1]+ input;
		}
	}

	for (int i = 0; i < m; i++) {
		int fromX, fromY, toX, toY;
		cin >> fromX >> fromY >> toX >> toY;
		//cout << v[toX][toY] << " - " << v[toX][fromY-1] <<" - " << v[fromX-1][toY] <<" + " <<  v[fromX-1][fromY-1] << " = ";

		cout << (v[toX][toY] - v[toX][fromY-1] - v[fromX-1][toY] + v[fromX-1][fromY-1]) << "\n";
	}
}