1. 왜 2-view geometry가 필요한가?

• 2D -> 3D 맵핑을 위해서는 3D-point의 깊이정보를 알아야 하고 이를 2D이미지로부터 얻기 위해서는 서로다른 두개의 관점에서 바라본 geometry가 필요하다.

• Localization에서 rigid body motion을 통한 pose를 알기 위해서는 2-view geometry가 필요하다.

2. Epipolar geometry

• 2-view geometry의 또다른 명칭.

2.1. Epipolar geometry의 구성요소들

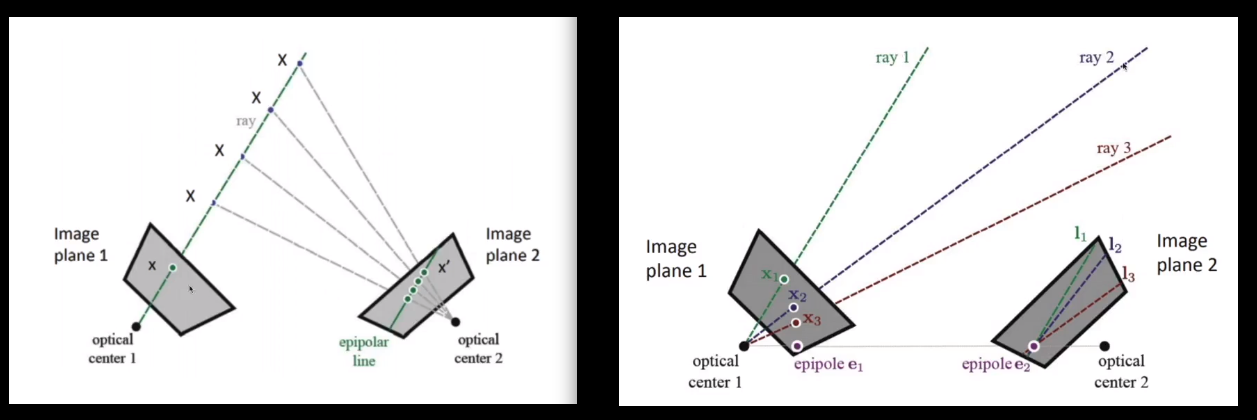
• ray: 3D point X를 이미지1로 사영할때 생기는 직선.
• epipolar line: ray를 이미지2로 재사영(reprojection)시 나타나는 직선.
  • 두 카메라가 함께 바라보고 있는 3d-point가 두번째 카메라 이미지 위에 나타나는 위치는 무조건 epipolar line 위에 있다.
• epipole: 여러개의 epipolar line이 교차하는 점.
  • 지난 시점의 카메라의 위치가 현 시점에서 보이는 경우 나타나게 된다.
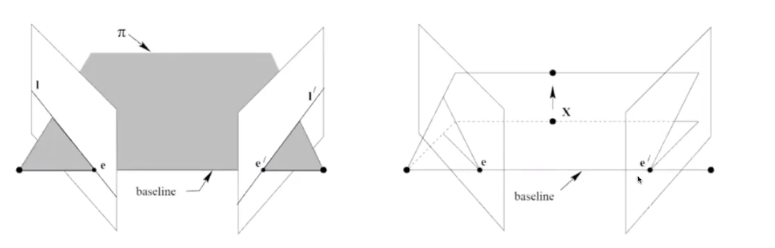
• epipolar plane: ray들과 두개의 optical center가 이루는 다각형.
• baseline: 두개의 optical center를 잇는 선.
• correspondence를 위한 세가지 조건
  • 3D point X는 무조건 epipolar plane위에 있어야한다.
  • 모든 epipolar line들과 baseline들은 epipole에서 교차해야한다.
  • 모든 epipolar plane들은 baseline을 포함해야한다.

2.2. 특별한 epipolar geometry 케이스

2.2.1. rotation이 없이 수평으로 translation만 있는 경우

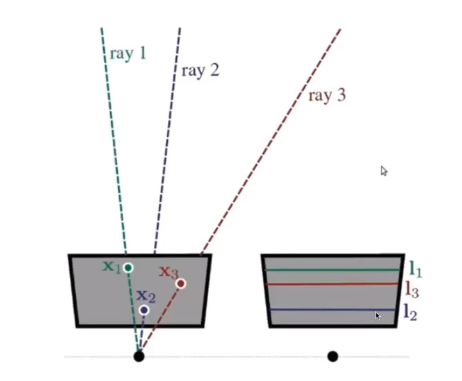
• epipole 존재x
• 모든 epipolar line들이 가로로 나타남.
• epipolar line들의 방향성이 수평으로 제한되기 때문에 각각의 ray의 대한 correspondence를 찾기 수월하여 스테레오 상황에서 pose 추정에 용이하다.

2.2.2. rotation 없이 전면으로 직진한 경우

• 각 카메라의 epipole 위치만으로도 카메라의 상대적 포즈변화를 알 수 있다.

3. Essential / Fundamental matrix

3.1. Essential matrix

두 카메라 사이의 회전(rotation)과 이동(translation)의 cross product로 이루어진 행렬로 두 카메라 이미지의 점들을 이용해 epipolar constraint를 구성해주는 역할을 한다.

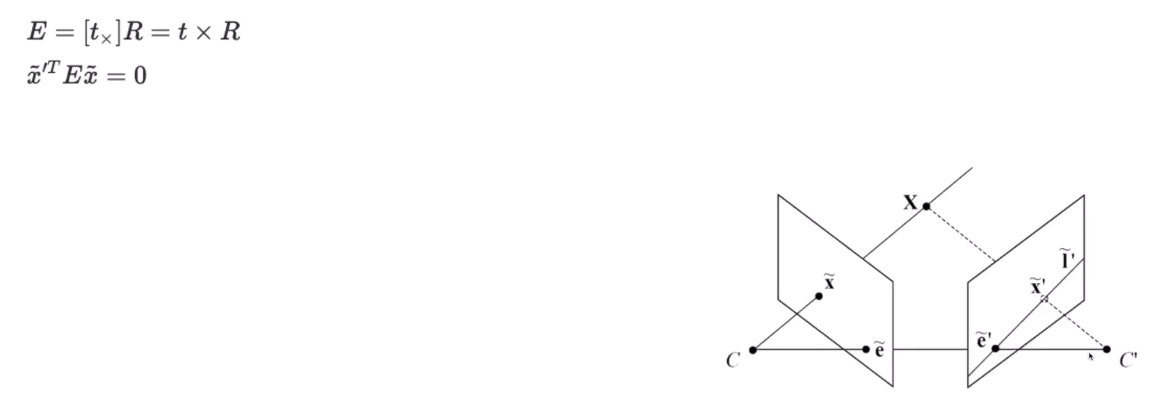
3.2. Fundamental matrix

Intrinsic matrix(K)를 적용한 essential matrix.
3.1.에서 적용된 x는 카메라좌표계 기준으로 flaot 형태로 표현되지만 실제 우리는 이미지 픽셀좌표로 표현해야 하므로 카메라 -> 이미지 캘리브레이션을 수행해야한다.

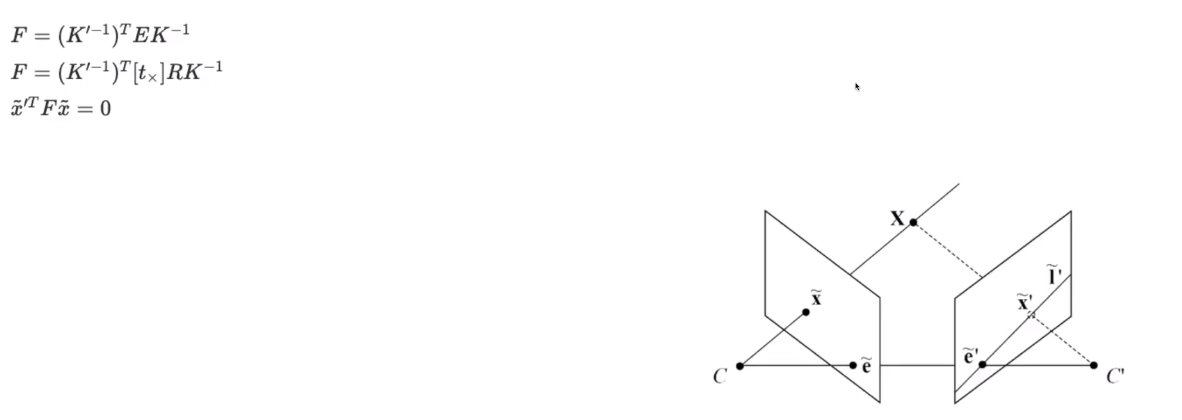
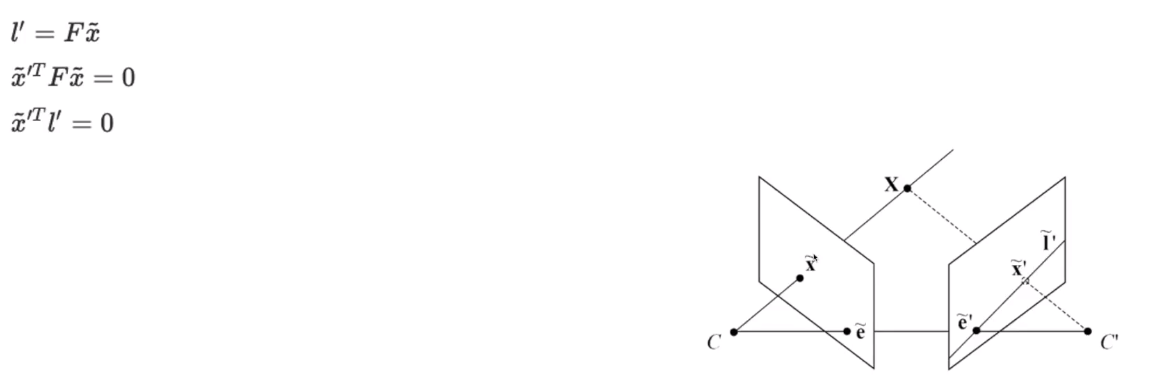
• F와 Epipolar line의 관계
  • F와 x를 곱하면 epipolar line 방정식을 얻을 수 있다.
  • x와 l을 곱하면 0이다.
    

3.3. E & F 행렬은 어떻게 구하는가?

• 5-point algorithm

  • Essential matrix는 최소 5개의 point correspondences가 있어야 구할 수 있다.
  • rotation{rx, ry, rz} + translation{tx, ty, tz} - scale정보{1} = 5 degrees of freedom을 갖는다.

• 8-point algorithm

  • Fundamental matrix는 최소 8개의 point correspondences가 있어야 구할 수 있다.
  • rotation{rx, ry, rz} + translation{tx, ty, tz} + intrinsic information{f, c} - scale정보{1} = 7 degrees of freedom을 갖는다.

• n degrees of solver는 문제를 해결하기 위해 필요한 최소 데이터 갯수가 n개라는 뜻이다.
  알고리즘에 필요한 데이터 갯수가 n이면 이를 minimal solve라 한다.

  • 5-point algorithm은 E를 구하기 위한 데이터 갯수가 5개이고 필요한 correspondences가 5개이므로 minimal solve라고 할 수 있다.
  • 8-point algorithm은 F를 구하기 위한 데이터 갯수가 7개이고 필요한 correspondences가 8개이므로 non minimal solve라고 할 수 있다.