Computing the Fundamental Matrix from Correspondences

초강송·2025년 2월 13일

Neural Fields & 3D 컴퓨터 비전

목록 보기

4/6

THE RED : Area Chair 이광무 교수의 Neural Fields & 3D 컴퓨터 비전 강의를 바탕으로 작성된 글입니다.

Retrieving the camera

Projective ambiguity

projective ambiguity는 서로 다른 카메라 설정이 동일한 fundamental matrix, F를 가질 수 있는 경우를 의미한다. 즉 epipolar 기하학에서 $x^TFx'=0$ 이 유지되는 한, 두 개의 카메라 설정이 모두 가능하다.

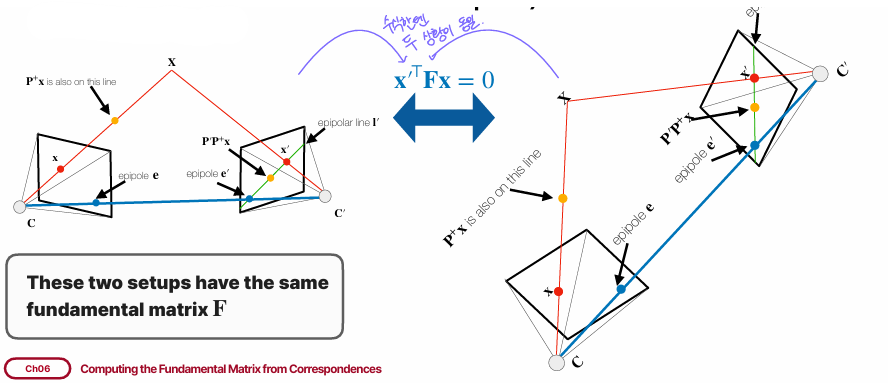
카메라가 보정된 상태(calibrated camera)에서는 projective ambiguity를 제거할 수 있지만, similarity ambiguity가 존재한다. 즉, 실제 크기가 큰 물체가 멀리 있는 건지, 작은 물체가 가까이 있는 건지를 구분할 수 없다.

Canonical form of camera matrices

이 ambiguity를 제거하기 위해 특정한 카메라 행렬을 선택하는 방법을 canonical form of camera matrices라고 한다. 즉, 두 개의 카메라 행렬을 아래와 같은 표준적인 형태로 변환하여, 불필요한 자유도를 제거한다.

첫 번째 카메라 $P = [I|0]$
두 번째 카메라 $P' = [[e']_x F|e']$

첫 번째 카메라는 원점에서 바라보는 기본적인, 단순한 형태로 설정되었고, 두 번째 카메라는 특정한 구조로 표현된 것을 알 수 있다.

두 번째 구조가 타당한지 검증하기 위해 fundamental matrix를 변형해 보자.먼저 $F = [e']PP^+$ 이므로 (이전 글 참고) P 자리에 P = $[I|0]$ 를, P' 자리에 $P' = [[e']_x F|e']$ 를 대입하면 사진과 같이 전개된다.

skew-symmetric matrix $[e']$ 끼리 곱한 값을 계산하면 $e'(e')^T - (e')^Te'I$ 결과가 나오고, $(e')^TF=0$ 이므로 식을 마저 전개하면 아래와 같이 나온다. $F = [e']PP^+$ 에 두 번째 카메라 행렬 $P'$ 을 대입하여도 같은 값 $\lambda F$ 가 나왔으므로(homogeneous system임) 설정된 두 번째 카메라 행렬이 타당하다는 것을 알 수 있다.

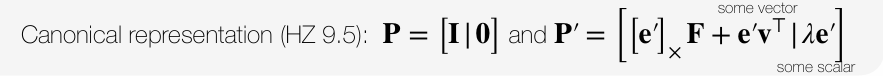
최종적으로 $P'$ 을 some vector와 scalar를 추가하여 나타낼 수 있다. vector는 두 번째 카메라의 추가적인 변환(회전 혹은 이동 등)을, scalar 값은 depth, 스케일 정보를 조정하는 값인데, 이 추가된 두 값은 전체적인 기하학적 관계는 방해하지 않는다.

Essential matrix

Essential Matrix, E는 정규화된 카메라(normalized camera) 사이의 관계를 나타내며 Fundamental Matrix, F와 달리 K(카메라의 내부 파라미터)가 제거된 상태에서 정의된다.

원래 우리가 알고 있는 카메라 투영식( $x= K[R|t]X_{world}$ )은 3D 점 $X_{world}$ 를 카메라 좌표계로 변환한 후, 내부 파라미터 $K$ 를 곱해 2D 이미지로 투영하는 과정을 의미하는 식이다.

우리가 좌표를 정규화(Normalized Coordinates)한다고 가정하면, 내부 파라미터 K가 사라지므로 아래와 같이 단순화할 수 있다.

$P = [I|0],\ P' = [R|t]$

그리고 우리는 다음 관계도 알고 있다.

$F = [e']PP^+$

위 관계를 정규화된 $P, P'$ 을 사용해 다시 표현하면 이 식이 바로 Essential Matrix를 정의하는 수식이 된다.

$E = [e']_xP'P^+ = [t]_xR$

카메라 내부 파라미터, K가 캘리브레이션되지 않은 상태에서(K는 임의의 값), 두 카메라 간의 관계를 찾는 문제는 Fundamental Matrix 문제이고, 내부 파라미터가 정규화되어 캘리브레이션된 상태에서( $K= I$ ), 두 카메라 간의 관계를 찾는 문제는 Essential Matrix 문제이다.

Cameras from the essential matrix

다음은 $Essential Matrix, E$ 를 분해하여 카메라의 R, t를 찾는 과정이다.

앞서 Essential matrix를 $E = [e']_xP'P^+ = [t]_xR$ 이렇게 정의했었다. 이때, $[t]_x$ 는 3x3 skew-symmetric matrix이므로 $[t]_x = S = kUZU^T$ 이렇게 나타낼 수 있다.

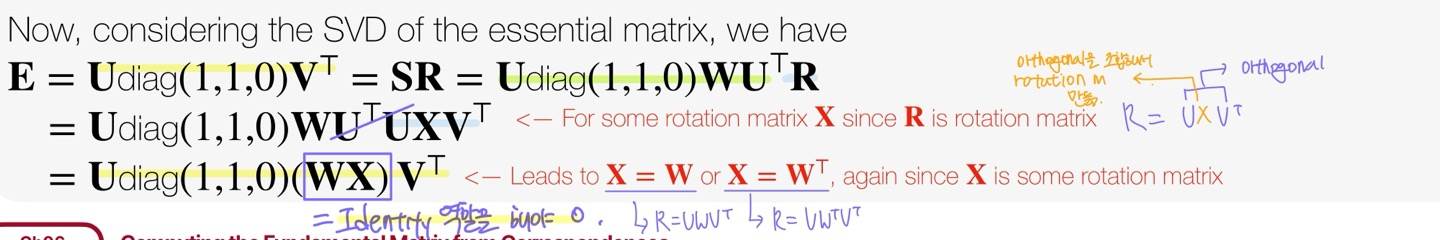
scale 값( $k$ )을 무시하고, $Z$ matrix를 $diag(1, 1, 0)W$ 로 표현하여 S에 관한 식을 다시 쓰면 $S = Udiag(1, 1, 0)WU^T$ 가 된다. 이제 이 값을 이용하여 $E$ 를 다시 표현하면 최종적으로 $Udiag(1, 1, 0)(WX)V^T$ 결과가 나온다.

이동 벡터 $t$ 는 skew-symmetric matrix이므로 $[t]_x$ 와 $t$ 를 곱하면 항상 0이 나온다. 이 점을 이용하여 $t$ 를 구할 수 있다. 즉, $t$ 는 $E$ 의 null space에 속하는데 $E$ 를 SVD한 결과가 $E=Udiag(1, 1, 0)WU^TR$ 이므로 t는 $U$ 행렬의 세 번째 열과 동일해야 한다. (부호는 알 수 없음)

Rotation matrix, $R$ 은 orthogonal matrix $U, V$ 를 이용해서 $UWV^T$ 혹은 $UW^TV^T$ 로 나타낼 수 있다.

최종적으로 이를 조합하면 4가지의 후보 $P'$ 이 나온다.

Chirality

위에서 얻은 4가지 $P'$ 에 대해 각각을 그림으로 나타낸 결과이다. 이 4가지 $P'$ 후보 중 실제로 물리적으로 가능한 카메라 구성을 선택하는 과정을 chirality test라고 한다.

Retrieving the fundamental matrix

Unnormalized eight-point algorithm

이제 fundamental matrix, F를 어떻게 구하는지 이야기할 차례이다. 소개해 주신 알고리즘은 Unnormalized eight-point algorithm으로 가장 기초적인 방법이다. (이 알고리즘을 실제로 적용하기에는 이 대응점( $x, x'$ )이 완벽하지 않기 때문에 문제가 발생할 것이다.)

$(x')^TFx = 0$ 수식을 풀어쓰면 $x'xf_{11}...$ 이런 식으로 나타낼 수 있다. 흥미로운 점은 이 수식을 우리가 알고 있는 값에 해당하는 부분과 모르는 값으로 나누어서 쓸 수 있다는 것이다. 이렇게 정리하면 익숙한 형태인 $Af = 0$ 꼴이 나온다. 이 식에 SVD를 적용하면 $f$ 를 구할 수 있다.

다만 이 A matrix는 ill-conditioned matrix이므로 normalization 과정(좌표들을 곱한 값이 특정 범위에 들어오게끔 하는 과정)이 반드시 필요하다.

Singularity constraint

이 외에도 고려해야 할 부분이 $Af = 0$ 이 완벽히 풀리지 않는다는 점이다. 즉 $f$ 가 매우 작은 숫자로 나오고 epipolar line이 한 점(=epipole)을 지나가지 않는 문제가 발생한다.

이는 $F$ 가 rank 2 constraint를 만족하지 않기 때문이다. 따라서 $F$ 를 rank 2 constraint를 만족시키는 $F'$ 으로 대체해야 하고, 이는 $F$ 를 SVD 분해했을 때 나오는 diagonal term의 $t$ 를 0으로 강제함으로써 수행 가능하다.

Normalized eight-point algorithm

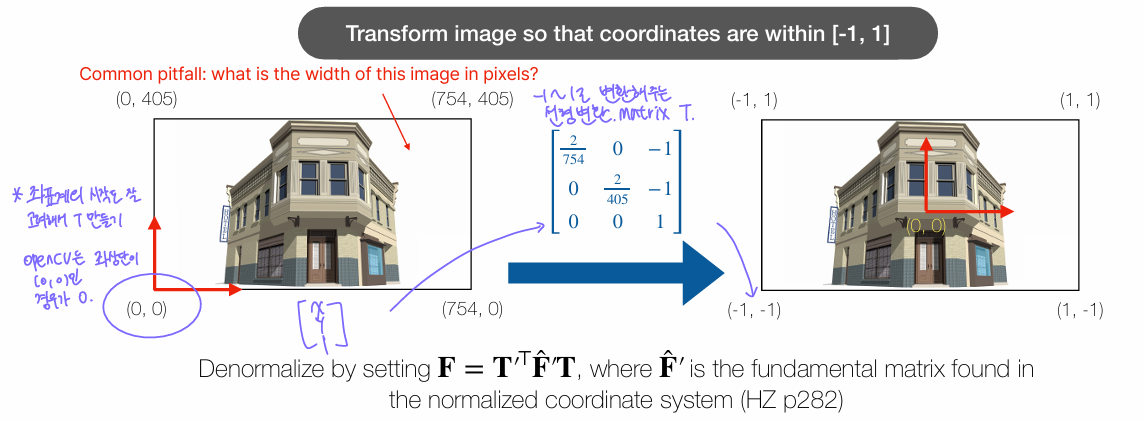
앞서 normalization 과정이 필요하다고 했는데 정확히는 아래와 같이 선형변환 matrix를 만들어서 수행할 수 있다. 이때 좌표계의 시작을 잘 고려해서 matrix를 만드는 것이 중요하다.

Robust estimation

실제로는 normalize를 해도 좌표에 noise가 존재한다. 따라서 normalize를 진행하고 noise가 최종 결과에 주는 영향을 최대한 줄이기 위해 robust estimation 과정을 거쳐야 한다.

일반적으로 robust estimation이라고 하면, RANSAC으로 대표되는데 이 알고리즘은 거의 모든 pose estimation, camera estimation에 다 들어간다.

Conclusion

The fundamental matrix

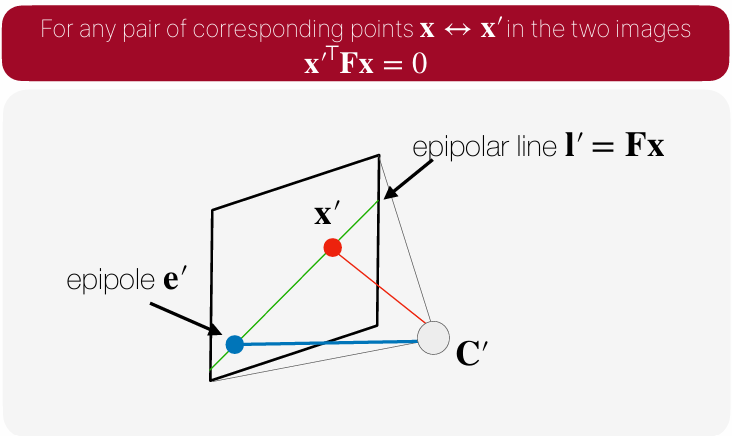
여태까지의 파트에서 가장 중요했던 것은 ${x'}^TFx = 0$ 이 수식이다. 이 수식을 통해 카메라 간의 연관관계를 설명할 수 있었고, fundamental matrix를 가운데에 두고 양쪽에 대응점을 곱했을 때 0이 되어야 한다는 게 epipolar geomatrix를 자체를 나타낸 수식이다라는 걸 명심하자.