Epipolar Geometry and the Fundamental Matrix

THE RED : Area Chair 이광무 교수의 Neural Fields & 3D 컴퓨터 비전 강의를 바탕으로 작성된 글입니다.

---

Epipolar geometry

두 개의 카메라를 사용하여 3D 공간의 물체를 촬영하고, 촬영된 2개의 2D 이미지를 이용하여 원래 3D 공간의 깊이(Depth)를 추정하고 싶다고 가정해 보자. 이때 한 이미지에서 어떤 점이 다른 이미지에서 어디에 대응되는지 모르면 3D 복원이 불가능하다. 즉, 두 이미지에서 같은 3D 점이 어디에 있는지 빠르게 찾는 방법이 필요한데, 이때 에피폴라 기하학(Epipolar Geometry)이 해결책이 된다.

Definition

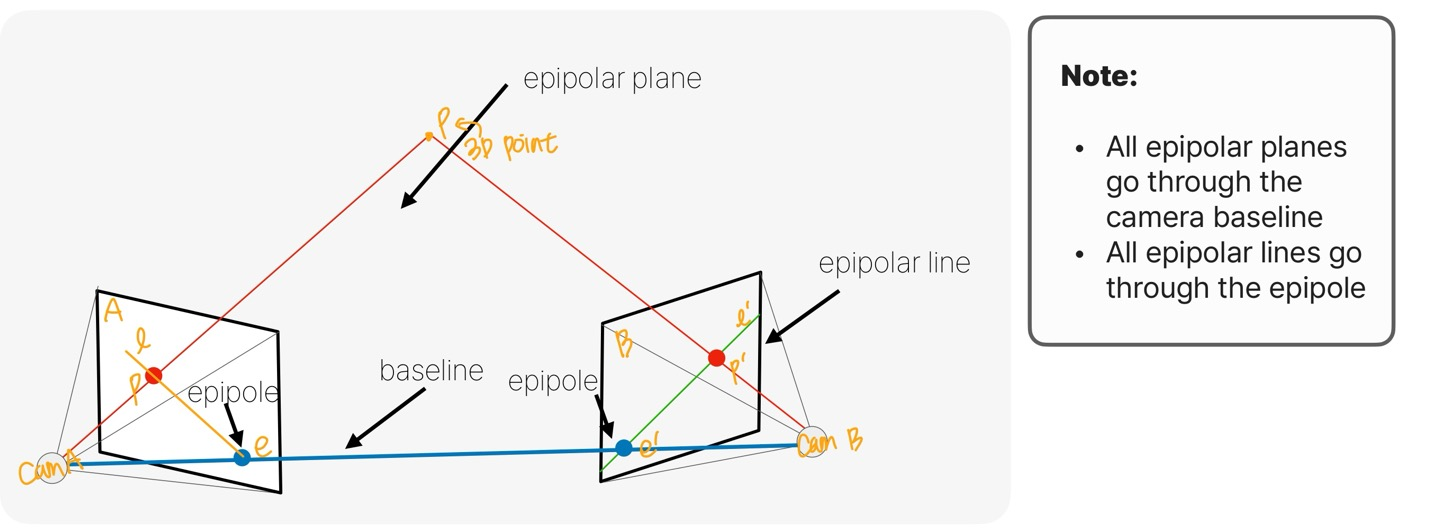
위 그림은 3D point $P$가 왼쪽과 오른쪽 영상에 투영된 모습이다. 이때 두 카메라 광학 중심을 잇는 선과 두 영상이 만나는 점 $e, e'$을 epipole이라고 하고, 투영점과 epipole을 잇는 직선 $l, l'$을 epipoloar line이라고 한다. 왼쪽 카메라와 오른쪽 카메라의 광학 중심 $e, e'$과 $P$로 구성된 평면은 epipolar plane이라고 하며, $e, e'$을 연결하는 직선을 baseline이라고 한다.

• epipole: 두 카메라 광학 중심을 잇는 선과 영상이 만나는 점
• epiploar line: 투영점과 epipole을 잇는 직선
• epiploar plane: 두 카메라 광학 중심과 3D point로 이루어진 평면
• baseline: epipole을 연결하는 직선

두 카메라 위치 사이의 기하학적 관계 [R|t]를 알고 있고 영상 A 위의 좌표 $p$를 알고 있을 때, 영상 B 위의 $p'$을 구하는 문제가 있다고 하자. 이때, 점 $P$까지의 거리(depth) 정보를 모른다면 $p$로 투영되기 전의 3차원 좌표 $P$를 복원할 수 없다. 따라서 $p'$ 또한 결정할 수 없다. 하지만 점 $P$는 A 카메라의 원점과 $p$를 잇는 직선 상에 존재하기 때문에 이 직선을 영상 B에 투영시키면 점 $p'$이 이 투영된 직선 위에 있음을 알 수 있다. 이 직선이 바로 epiploar line, $l'$이다.

정리하면, A의 영상 좌표 $p$로부터 대응되는 B의 영상 좌표 $p'$을 유일하게 결정할 순 없지만, $p'$이 지나는 직선인 epipolar line $l'$은 유일하게 결정할 수 있다.

https://darkpgmr.tistory.com/83

Converging cameras

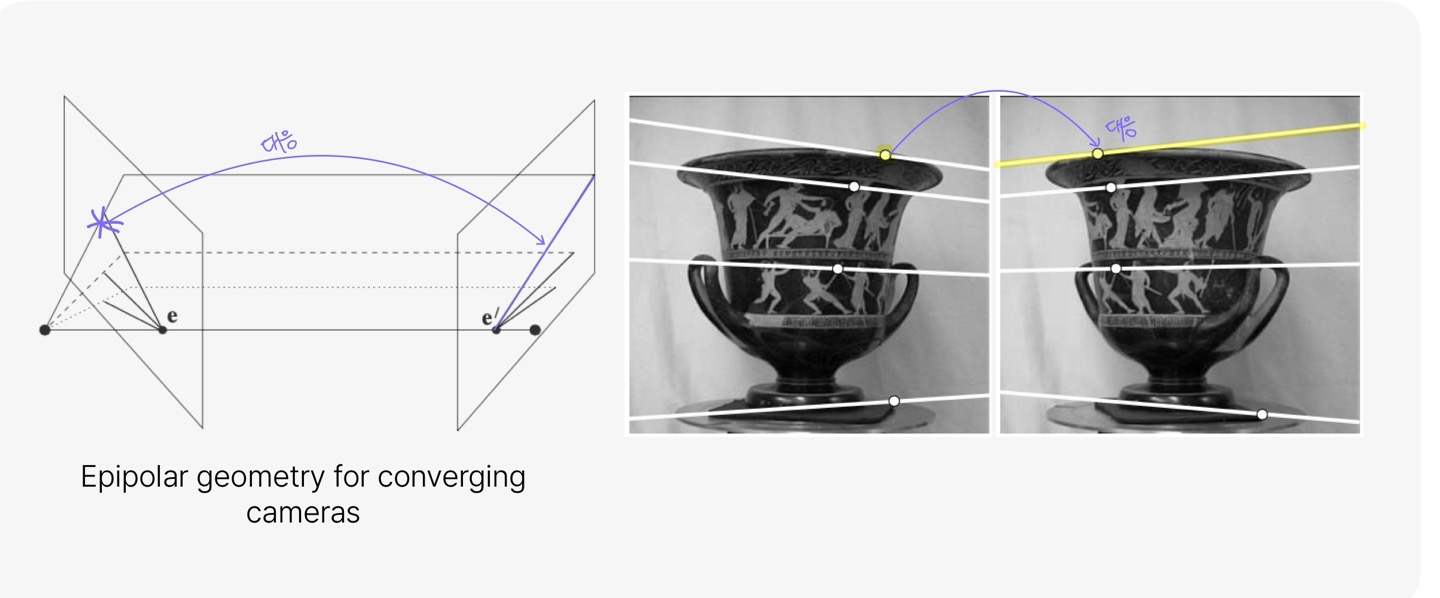
앞서 그림으로 표현한 것을 실제 이미지로 나타내면 위와 같다. 왼쪽 이미지의 한 점이 오른쪽 이미지의 선에 대응되는 것을 알 수 있다.

A bit more formally - 3D point X와 C를 이은 직선

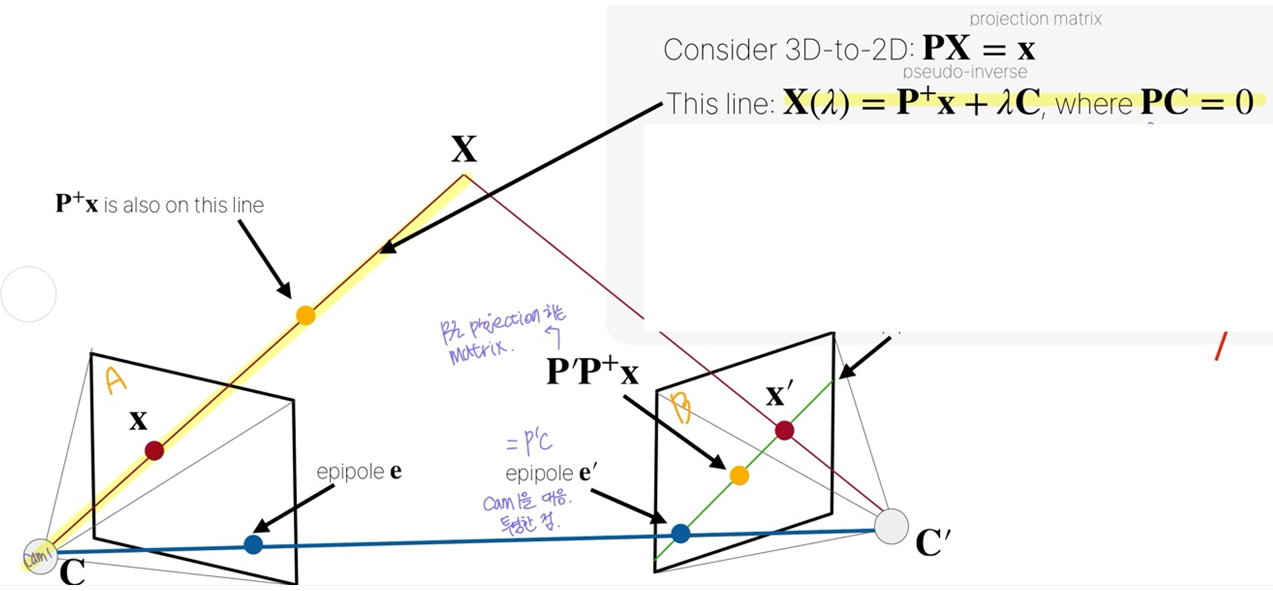
다음으로는, 이 시스템을 수식적으로 설명해 보자. 3차원에 있는 어떤 좌표 $X$가 각 이미지에 projection 된 좌표를 $x, x'$라고 하고, 왼쪽 이미지로 $X$를 projection시키는 matrix를 $P$라고 하자. 여기서 P가 바로 K[R|t] matrix이다. 이렇게 변수를 설정했을 때, C와 $X$를 잇는 선은 $X(\lambda)=P^+x + \lambda C,\ (PC = 0)$ 로 나타낼 수 있다.

이 식을 통해 3D 점이 2D로 투영될 때 변하지 않는 속성과, 점이 무한히 멀어질 때의 방향을 설명할 수 있다.

• 3D 점이 2D로 투영될 때 변하지 않는 속성

  먼저 $X(\lambda)=P^+x + \lambda C,\ (PC = 0)$ 식의 양변에 $P$를 곱해 보자. $P^+$는 $P$의 pseudo-inverse이므로 $PP^+=I$가 되고, $^1$$PC=0$이 되기 때문에 $PX(\lambda)=x$가 된다.

  즉, 어떤 $\lambda$ 값을 선택하든지, 3D point $X(\lambda)$가 투영되면 항상 같은 점 $x$가 나온다. 이를 통해 같은 2D 투영을 가지는 3D 점은 무한히 많으며 모두 카메라 같은 직선 위에 존재한다는 것을 알 수 있다.

  $^1$P는 3d 점 X를 2D 이미지 평면의 점 x로 사용하는 행렬이다. 그러나, 카메라 중심 C를 여기에 대입하면 어떻게 될까?

  카메라 중심은 이미지 평면에서 정의되지 않는 점이다. (카메라가 3D 점을 보는 것은 가능하지만, 카메라는 자체는 자신의 시야 안에서 자신을 볼 수 없다.) 즉, 카메라 중심은 광선들이 시작하는 점이므로, 어떤 유한한 $x$ 좌표로 투영될 수 없다.

  이것은 수학적으로 $PC=0$이 되어야 함을 의미한다. 즉, 카메라 중심은 투영 행렬 $P$의 널 공간에 존재하기 때문에, 이미지 평면에서 정의되지 않는 것이다.

• 점이 무한히 멀어질 때의 방향

  이번에는 양변을 $\lambda$로 나누고 $\lambda \to \inf$로 보내보자. 첫 번째 항인 $\frac{P^+x}{\lambda}$는 0으로 가서 없어지고, 두 번째 항만 남을 것이다. 즉 최종 식은 $\lim_{\lambda \to \infty}X(\lambda) = C$이 될 것이다.

  이를 통해 무한히 멀어지는 점의 방향은 결국 카메라 중심을 향한다는 것을 알 수 있다. 이 부분이 잘 와닿지 않아서 이해를 도울 수 있는 내용을 아래에 적어 두었다.

  우리가 궁금한 것은 '방향'이므로 이 무한히 멀어지는 점을 정규화해서 크기가 1인 방향 벡터를 확인해 보자.

  $||X(\lambda)\| = \| P^+ x + \lambda C \|$

  $P^+ x$는 변하지 않는 상수 벡터이지만, $\lambda C$는 $( \lambda)$ 가 커질수록 점점 더 커진다. 즉 $( \lambda)$가 아주 커지면 $( \lambda)$ 항이 지배적이 된다는 것이다.

  $||X(\lambda)\| \approx \| \lambda C \| = \lambda \| C \|$

  여기까지 유도한 뒤 정규화를 진행해 보면, 아래와 같이 나타낼 수 있다.

  $\lim_{\lambda \to \infty} \frac{X(\lambda)}{\|X(\lambda)\|} = \frac{C}{\|C\|}$

  즉 무한히 멀어지는 점을 정규화하면, 방향 벡터가 $C$와 같은 방향을 가지게 되며, $C$가 마치 방향 벡터처럼 보인다. 즉, 무한히 멀어지는 점의 방향 벡터가 카메라 중심을 향하게 되는 것이다.

A bit more formally - epipoloar line l'

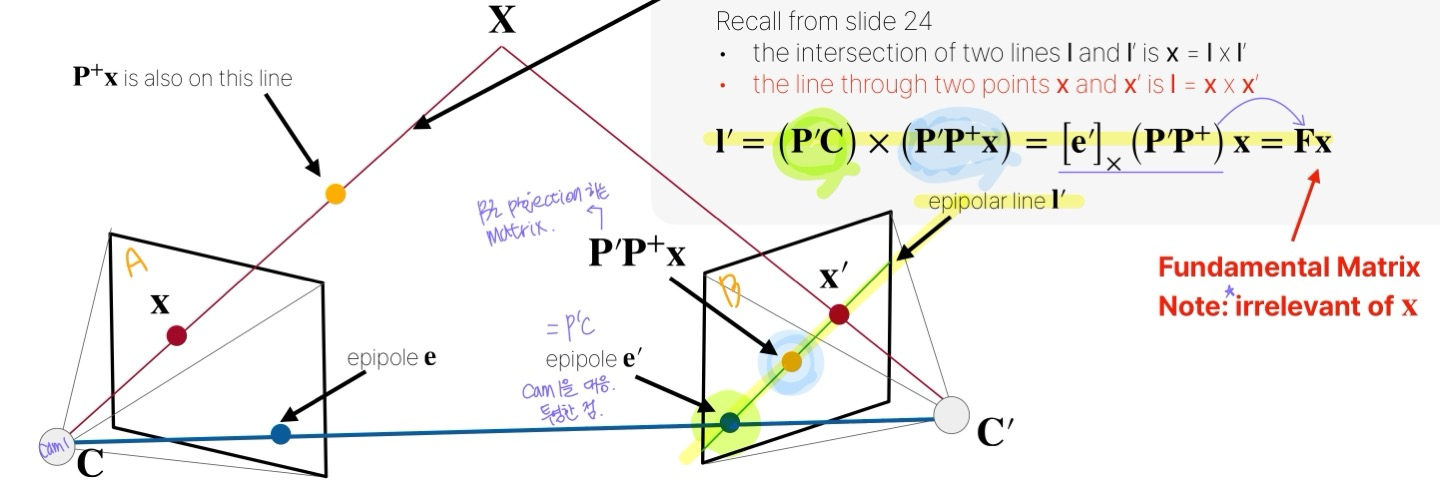
이전에, 어떤 line $l$ 위에 있는 두 점을 외적하면 line $l$을 구할 수 있다는 개념을 리마인드해 보자. 3d 점 $X$를 오른쪽 2D 이미지 평면의 점 x로 투영하는 행렬을 $P'$이라고 했을 때, line $X(\lambda)$ 위에 있는 점 $P^+x$를 오른쪽 이미지 B에 projection 한 점은 $P'P^+x$ 이렇게 나타낼 수 있다. $^2$또 왼쪽 카메라를 오른쪽 이미지 B에 투영한 점은 $P'C$가 되고 이 점은 epipole $e'$을 의미하므로, 두 점을 외적한 결과는 $l' = (P'C)*(P'P^+x) = [e']*(P'P^+)x$가 된다.

$x$에 전혀 영향을 받지 않는 부분인 $[e']*(P'P^+)$을 $F$로 바꾸어 epipolar line을 $l' = Fx$로 나타낼 수 있다. 즉, 한 영상의 좌표를 이용하여 다른 영상에서의 대응되는 epipolar line을 계산할 수 있도록 해주는 변환 행렬을 Fundamental Matrix라고 한다.

$^2$ epipole을 앞에서는 두 카메라 광학 중심을 잇는 선과 영상이 만나는 점으로 정의했다. 그렇지만 이 epipole을 한 카메라의 광학 중심이 다른 카메라의 이미지 평면에 투영된 점이고도 정의할 수 있다.

Since the optical centers of the cameras lenses are distinct, each center projects onto a distinct point into the other camera's image plane. These two image points, denoted by $e_L$ and $e_R$, are called epipoles or epipolar points.

https://en.wikipedia.org/wiki/Epipolar_geometry

Correspondence condition

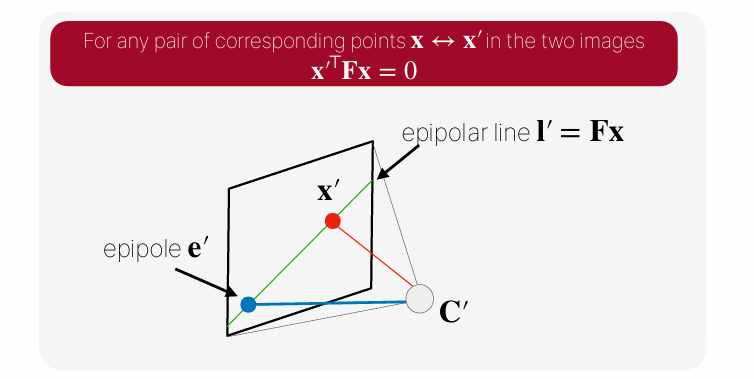
epipolar line과 이미지에 투영된 점을 내적하면 그 결과는 0이 된다. 이를 수식으로 나타내면 다음과 같다.

$(x')^TFx=0$

이 관계는 fundamental matrix, $F$가 epipolar geometry를 요약하는 핵심 수식임을 보여준다.

fundamental matrix, $F$는 두 이미지에서 대응되는 점들 간의 관계를 나타내는 3×3 행렬로, 특정한 점 $x$에 의존하지 않는다. 즉, 어떤 이미지 좌표 $x$를 선택하더라도, 그에 대응하는 점 $x'$은 반드시 위 수식을 만족해야 한다. 이로부터 어떤 점 $x$를 선택하든, 그 점에 대응하는 모든 점 $x'$은 반드시 특정한 epipolar line 위에 위치해야 한다. 라는 geometric constraint을 얻을 수 있다.

fundamental matrix, $F$는 대응되는 점들이 반드시 epipolar line 위에 위치하도록 강제하고, 모든 epipolar line은 결국 epipolar plane 위에 존재하므로, 대응되는 모든 점들은 결국 baseline을 포함하는 epipolar 평면 안에서 움직이게 된다. 다시 말해, fundamental matrix, $F$이 강제하는 geometric constraint 때문에 모든 대응점들이 하나의 epipolar 평면을 따라야 한다.

Some useful facts

$F$ is unique for a pair of images (cameras)
: 두 개의 이미지가 주어졌을 때 두 이미지 사이의 관계를 나타내는 fundamental matrix는 유니크하다.

Transpose: if $F$ is a fundamental matrix for $(P, P')$, then $F^T$ is a fundamental matrix for $(P', P)$
: 만약 $F$가 카메라 $(P, P')$에 대한 fundamental matrix(=첫 번째 이미지에서 두 번째 이미지로 가는 matrix)라면 $F^T$는 $(P, P')$에 대한 fundamental matrix(=두 번째 이미지에서 첫 번째 이미지로 가는 matrix)이다.

Epipolar line: $l' = Fx$ and $l = F^Tx$

$F$ is a projective mapping from a point $x$ to line $l'=Fx$

Epipoles: all epipolar lines go through them, thus $(e')^TFx = 0, (e')^TF = 0 \ and \ Fe = 0$
: 임의의 x에 대해 모든 epipolar line은 epipole을 통과한다. 이는 $(e')^TF$ 혹은 전치한 결과 $F^T(e')$가 항상 0이 되어야 한다는 것을 의미한다. 마찬가지로 다른 이미지에서 epipole e에 대해서도 같은 원리($Fe = 0$)가 성립한다. 이 말은 다시 말하면, 이 epipole이 F의 null space에 속하는 vector라는 것을 의미한다.

F has 7 degrees of freedom, 3 x 3 - 1(homogeneous) - 1(rank 2)
: fundamental matrix는 homogeneous 좌표계에서 정의돼 있기 때문에 scale에 영향을 받지 않는다. 또 $^3$fundamental matrix $F$는 epipolar geometry의 관계를 만족하기 위해 항상 rank가 2인 행렬이어야 한다. 즉, def(F)=0이 되어야 한다는 제약 조건이 있다. 따라서 자유도가 9가 아닌 7이다.

이는 앞서 살펴 보았던 homography보다 제한적이다. 3차원적으로 의미가 있는 변환만 유효한 변환으로 취급한다고 해석할 수 있다.

$^3$ fundamental matrix, F의 rank가 2이면, null space가 1차원이 된다. 즉 $Fe = 0$을 만족하는 epipole, $e$가 정확히 1개만 존재하게 되고 epipole은 모든 epipolar line, $l$의 교차점이 된다. (모든 epipolar line이 epipolar를 지난다는 것은 $e(l) = e(Fx)=0$이 모든 $x$에 대해 항상 성립한다는 것을 의미한다. 여기서 $Fe =0$이므로 해당 식은 항상 성립한다.)
즉 fundamental matrix, F의 rank가 2여야만 epipole이 정확히 하나 정의되고 모든 epipolar line이 이 점을 지나게 된다.