Homogeneous Coordinates and 2D Homography

THE RED : Area Chair 이광무 교수의 Neural Fields & 3D 컴퓨터 비전 강의를 바탕으로 작성된 글입니다.

---

Homogeneous coordinates

Parameterizing a line

특정 물리적 지점에서 카메라까지 어떻게 빛이 이동하는지를 모델링하기 위해 가장 처음 시작해야 될 것은 '빛이 이루는 특정 선을 어떻게 수학적으로 표현할 것인가'이다.

x, y 평면 상에 한 선분이 있다고 할 때 이 선분을 표현하는 수식은 ax + by + c = 0으로 표현할 수 있다. 이 부분에 선형대수를 도입하기 위해 ax + by + c1 = 0으로 식을 약간 수정하면, 이 선분을 벡터 두 개의 선형곱으로 나타낼 수 있게 된다.

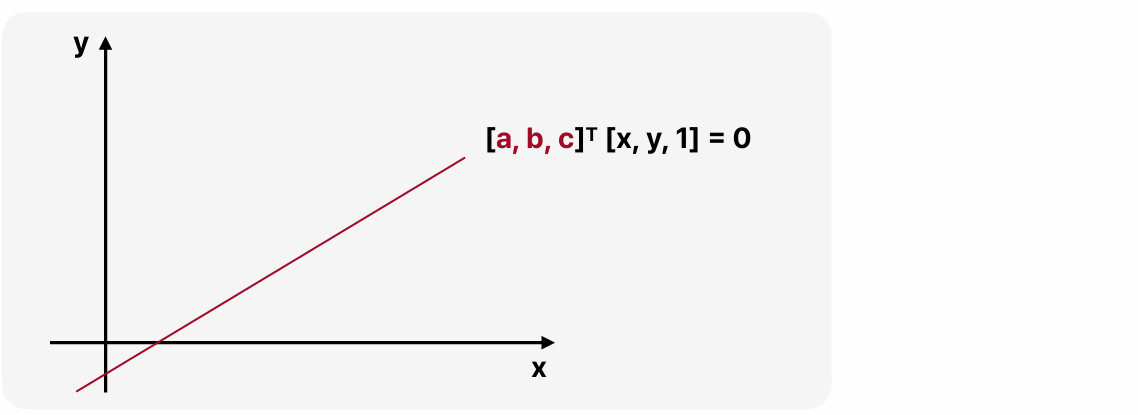
선분을 벡터 두 개의 선형곱으로 나타냈을 때, [x, y, 1] 부분에 어떤 값의 k를 곱하든 이 등식에 영향을 주지 않는다.

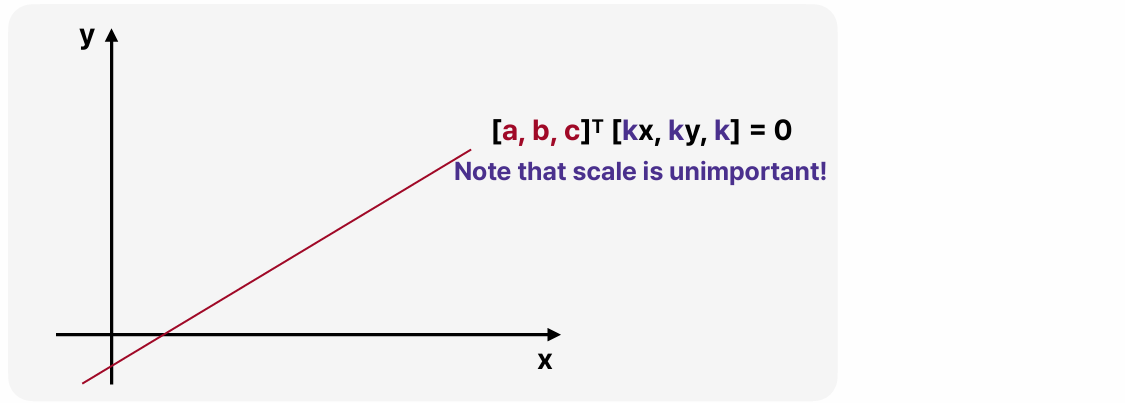
k를 카메라와 사물을 잇는 연장선 산에서 사물이 얼마나 많이 떨어져 있는지를 나타내는 거리를 의미한다고 생각해 보자. 즉, 실제로 사물이 카메라로부터 얼마나 멀리 있는지의 정보를 k라고 해 보자. 이때 카메라로 빛이 들어오는 경로가 동일하기 때문에 그 경로 상에서 실제 거리(k)가 달라지더라도 동일한 영상에 사물이 맺히게 된다.

선분을 벡터 두 개의 선형곱으로 나타내는 방식으로 방정식을 구성하게 되면 위와 같은 물리적인 현상을 수학적으로 설명하기에 매우 유리한 측면이 있다. 카메라는 3D 공간의 점을 2D 평면으로 투영하는데, 이 투영 과정에서 거리 정보(k)는 영향을 주지 않는다는 것이 (=단지 방향 정보만 남는다는 것이) 수식을 통해 명확하게 반영되기 때문이다.

이와 같이 스칼라 곱에 불변한 좌표계를 Homogeneous coordinates system이라고 하며, 점을 $x= [x, y, 1]$ 같은 형태로 나타낸다.

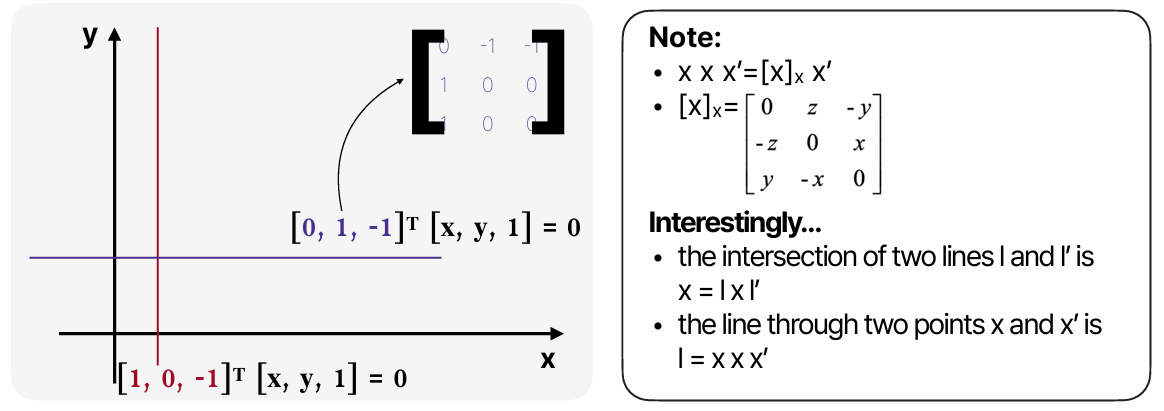
이 좌표계에는 몇 가지 특징이 있다. 어떤 선분을 구성하는 vector, $l = [a, b, c]$가 있다고 하고, 그 선분 위의 모든 점들을 $x=[x, y, 1]$로 표현한다고 할 때 아래와 같은 성질이 성립한다.

1. 두 선분의 외적은 두 선분의 교차점을 의미한다.
2. 두 좌표의 외적은 두 좌표를 지나는 선분을 의미한다.
3. 자기 자신과의 외적은 0이다.

이러한 수학적 편의성 때문에 Homogeneous coordinates system이 널리 사용된다고 볼 수 있다.

두 선분의 외적은 아래 이미지에서 보이는 외적 matrix를 만들어서 사용할 수 있다. 즉 $x$라는 vector가 $(x, y, z)$로 표현될 때 해당 matrix를 이용하면 vector 간의 외적을 matrix와 vector의 선형적인 연산으로 표현할 수 있다.

2D Homography

From one image to the other

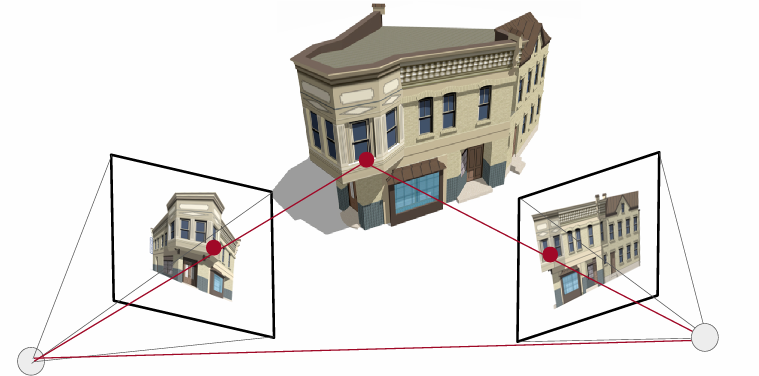
위 그림을 보며 이해하려고 할 때, 3D 물체와 2D 이미지 사이의 관계를 explicit 하게 설명하는 것은 어렵다. 즉, 3D 지점과 2D 지점 간의 변환을 명확히 정의하기가 어렵다는 것이다. 이런 이유로 관계를 명확하게 수식으로 표현하지 않고 주어진 3D와 2D 지점들이 특정 물리적 설정(카메라 모델, 투영 원리 등)을 만족하는지 여부를 판단한다. 예를 들어, 3D 지점과 2D 지점이 주어진 카메라 매트릭스에 의해 투영된 결과와 일치한다라는 식으로 특정 조건을 만족하는지 확인한다. 이를 implicit한 정의라고 한다.

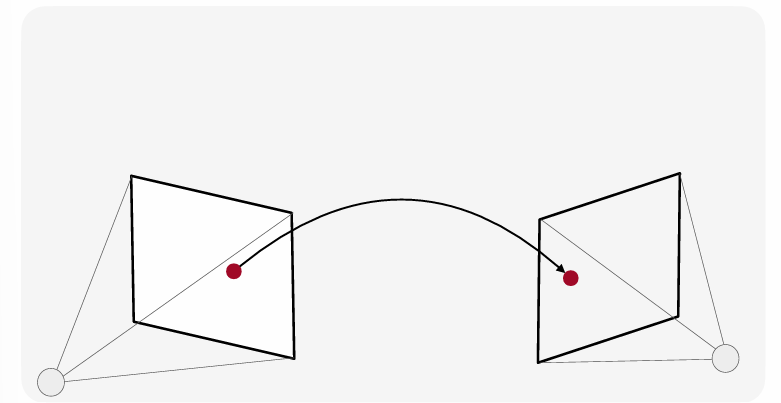
그래서 먼저 설명하신 게, 2D Homography이다. 2D Homography란, 3차원 모델을 거치지 않고 한 지점에서 다른 지점으로 직접적으로 이동하는 변환 방식이다. 이 경우에는 2D 좌표계 상에서 하나의 점이 다른 2D 좌표로 이동하는 것을 표현한다.

• 8 자유도의 homography 변환
  

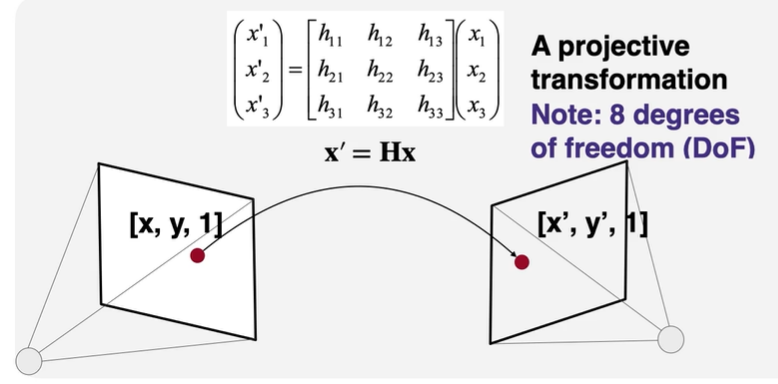
Homogeneous 좌표계를 사용하여 두 평면상의 점을 나타냈을 때, 두 좌표간 projective 변환을 표현하는 matrix를 2D homography라고 한다. 이 matrix는 9개의 숫자로 이루어져 있긴 하지만, 연산 이후 마지막 차원의 값을 1로 만들어 주어야 하므로 변환의 자유도는 8개이다.

(자유도(=Degrees of Freedom, DoF)란 변환을 표현하기 위해 필요한 최소한의 독립적인 매개변수 개수이다.)

Other 2D transformations

보다 좀 제한된, 다양한 변환들이 서브 변환들로 존재한다.

• 2 자유도 Translation
  ${x'}_1 = x_1 + tx$, ${x'}_2 = x_1 + ty$
  

• 3 자유도 Euclidean 변환
  $t$ 각도로 물체 회전 (1가지 자유도)
  $t_x, t_y$로 물체 이동 (2가지 자유도)
  

• 4 자유도 Similarity 변환
  

• 6 자유도 Affine 변환
  

Affine 변환에서는 기울어지는 현상이 일어나는 것 외에 실질적으로 3차원 물체가 일으킬 수 없는 변환도 표현되기 시작한다. 6 자유도 Affine 변환에서 벌써 이런 현상이 발생한다는 것은 8 자유도의 homography 변환에서는 더 심할 수도 있다는 것을 의미한다.

그렇지만 이 homography가 3차원을 설명 못하기 때문에 쓸모 없는 것은 아니다. 예를 들어 고정된 카메라에서 아주 먼 상황을 볼 경우에는, 원근감의 영향을 크게 받지 않기 때문에 homography 변환만으로도 2D 평면 간의 변환을 간단히 설명할 수 있다.

Finding H via Direct Linear Transformation (DLT)

그렇다면 이 $H$는 어떻게 구할 수 있을까? 여기서 소개해 주신 가장 기초적인 방법은 DLT이다. 실제로는 노이즈가 많이 끼는 방법이라 사용하진 않지만 나중에 딥러닝과 융합할 때 이 방법이 유효하기 때문에 소개해 주셨다.

$x' = Hx$ 식을 아까 보았던 자기 자신과의 외적은 0이다. 성질을 이용하여 $x'$ x $Hx = 0$으로 변환한다. 마찬가지로 앞에서 소개했던, 외적 matrix를 사용하여 vector 간의 외적을 matrix와 vector의 선형적인 연산으로 표현해 준다. 이후 $H$ matrix를 축약해 주면 아래와 같은 단계까지 올 수 있다.

(내가 아는 변수 matrix) x (내가 모르는 변수) = 0 이라는 standard한 선형 수식 form이 나왔다. 안타까운 소식은 첫 matrix의 마지막 row는 나머지 두 row를 잘 조합하여 만들 수 있기 때문에 의미가 없다. 결국 최종적으로 정리를 하면 아래와 같이 나온다.

여기서 $h$가 0이 되어도 해당 등식은 만족하지만, $h$가 0이 된다는 것은 두 카메라를 무한대 거리만큼 떨어뜨린 것과 같다. 따라서 의미를 부여하기 위해 h의 norm이 1이다를 가정하고 문제를 풀게 된다. homogeneous 좌표계에서 스칼라곱은 의미가 없다는 것을 다시 활용하는 것이라고 볼 수 있다.

$Ah = 0$ 이 수식을 풀기 위해서 SVD 방법을 사용하면 $h$에 대한 문제가 자동으로 풀린다.

여기서부터는 이해하면 좋지만 윗 내용만 기억하고 넘어가도 좋은 부분이다.

주어진 $Ah = 0$과 $||h||=1$이라는 제약 조건을 만족하는 $h$를 찾기 위해 라그랑지안 L을 설정하고, KKT 조건을 적용한다. 이 조건에 따라 L의 최적 해는 다음 조건을 만족해야 한다.

1. $\nabla_h \mathcal{L} = 0$

해당 조건을 풀고자 하는 문제에 적용하면 아래와 같이 전개해 나갈 수 있다.

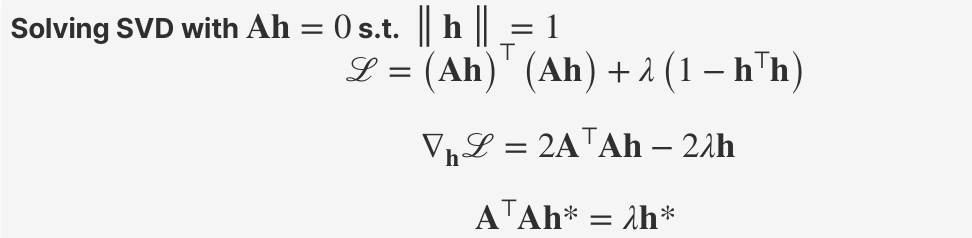
$A^TAh = \lambda h$ 과 같은 형태는 일반적인 eigenvalue problem와 동일한 형태이다. 즉, $A^TAh = \lambda h$ 식을 만족하는 해 중에 eigenvalue, $\lambda$가 가장 작은 것에 대응하는 eigenvector, $h$를 구하는 것과 동일한 문제가 된다.

DLT does not give the best geometric solution

DLT 방식과 관련하여 기억해야 할 두 가지가 있다.

첫 번째는 DLT의 문제점이다. 우리가 찾고 싶은 $h$는 한 이미지에서 다른 이미지로 포인트를 보냈을 경우 원래 가야 할 위치로 제일 잘 가는 $h$이다. 그러나 DLT solution(=Algebraic solution)의 문제점은 DLT는 $||Ah||=||x'$ x $Hx||$를 최소화하는 $h$를 찾는 것이지, 우리가 알고 싶은 $||x'$ - $Hx||$를 최소화하는 $h$를 찾지 않는다는 것이다. 그렇지만 이 operation은 미분 가능한 operation이기 때문에 deep network에 적용하기 쉬워서, 이 문제점에도 불구하고 해당 방식을 많이 사용한다고 한다.

Normalization is important

또 하나는 DLT는 $Ah = 0$ 꼴의 문제를 푸는데 안타깝게도 대다수의 $A$ matrix는 ill-condition이라고 부르는 상태가 된다. 즉 한 matrix 안에 0에 가까운 숫자와 매우 큰 숫자가 공존하게 되는데 그렇게 되면 컴퓨터 안에서 이 matrix 관련 연산을 할 때 문제가 발생한다. 따라서 이 문제를 해결하기 위해서는 좌표를 0~1 사이로 normalize 해 주어야 한다.