The Pinhole Camera Model and Camera Pose

THE RED : Area Chair 이광무 교수의 Neural Fields & 3D 컴퓨터 비전 강의를 바탕으로 작성된 글입니다.

---

The Pinhole Camera Model

From 2D to 3D

이제는 3차원 좌표 표현을 사용한다. 아래 자료는 3차원 세계의 점이 카메라 렌즈를 통해 2차원 이미지 plane으로 투영되는 장면이다. plane 위에 있는 좌표는 homogeneous 좌표처럼 보이지만, 카메라 초점 거리 $f=1$에서 빛이 이미지 plane과 교차하는 지점을 나타내는 3차원 좌표이다.

The pinhole camera model

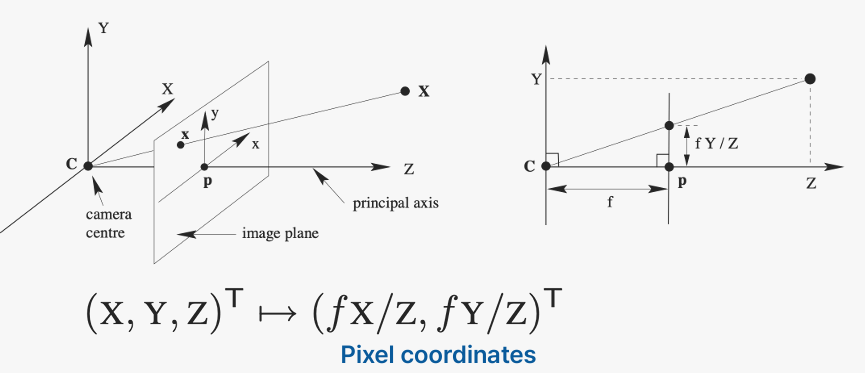
pinhole 카메라를 사용하였을 때 실제 3차원 좌표가 image plane 상에서는 어떤 좌표로 형성될까?

이미지 평면 위의 좌표를 $x',\ y'$이라고 할 때, $y'$ 좌표는 초점 거리 $f$를 밑변으로 한 삼각형의 높이와 관련이 있다. 따라서 $y' = f + tan\theta = f* \frac{Y}{Z}$로 나타낼 수 있다. 이 방법은 $x$ 좌표 계산에도 동일하게 적용되며, $x' = f * \frac{X}{Z}$로 나타낼 수 있다.

지금 결과는 카메라를 (0, 0)으로 편의상 고정했다는 가정 하에 계산된 결과이다.

이 과정을 homogeneous 좌표계를 사용하면 아래와 같이 수식으로 간단하게 나타낼 수 있다. 앞서 배운 homogeneous 좌표계의 중요한 특징 중 하나는 좌표 전체에 동일한 상수를 곱해도 본질적으로 같은 좌표로 간주된다는 것이다. 여기서는 pixel coordinates를 homogeneous 좌표계로 나타내기 위해 마지막 차원으로 1을 추가하고, 모든 좌표값에 Z를 곱해서 나타낸 것을 알 수 있다.

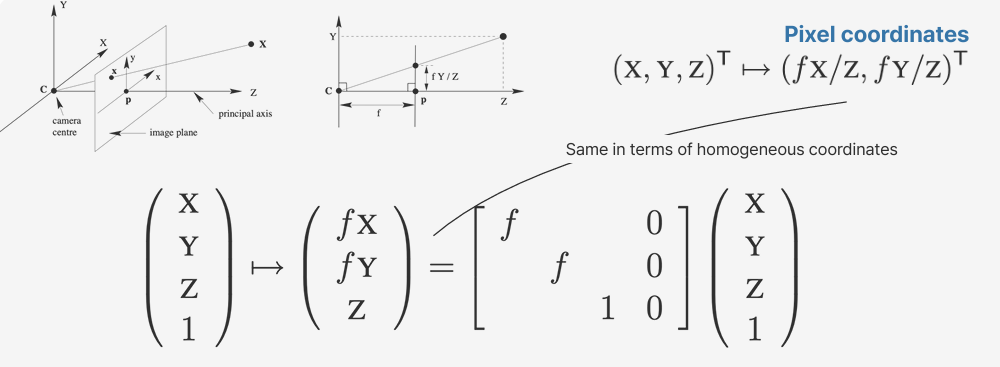
만약에 카메라 중점이 (0, 0)이 아니고 옮겨진 상태라면 $(X, Y, Z)^T$ 좌표도 $(fX/Z + px, fY/Z + py)^T$ 이렇게 옮겨주면 된다. matrix로 아래와 같이 수정하면 된다.

이 matrix의 왼쪽 3x3 부분을 카메라 calibration matrix라고 하고 카메라에 대한 대부분의 것들을 표현한다고 생각할 수 있다. 그리고 이 전체 표현을 $x = K[I|0]X_{cam}$ 이렇게 표기할 수도 있다. 2D 좌표를 $x$, 3D 좌표를 $X_{cam}$으로 나타냈으며 K를 Identity, 0 행렬에 곱하였다는 의미이다.

여기서 주의할 점은 이 수식은 3차원에서 2차원으로 가는 수식이지 2차원에서 3차원으로 가는 수식은 아니라는 것이다.

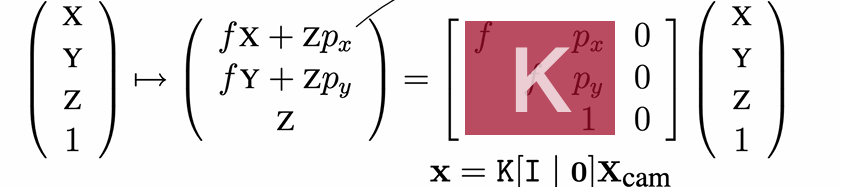
Pinhole vs actual camera

실제 카메라는 빛이 일직선으로 가는 게 아니라 렌즈를 통해서 가게 된다. 그리고 렌즈를 통해서 빛의 굴절 정도가 달라지며 왜곡이 일어나기도 한다.

아래 그림의 점선으로 표시된 부분을 보면 직선으로 나타나야 할 것들이 휘어져 보인다. 이걸 Radial distortion이라고 부르는데, 이것까지 보정을 해 주면 오른쪽처럼 나온다.

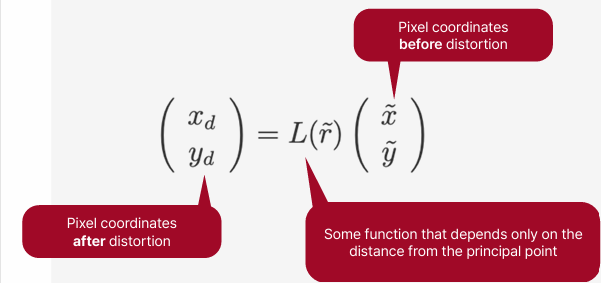
Radial distortion이 일어난 좌표는 다음과 같은 함수로 모델링할 수 있다.

이 왜곡이 3차원 vision에서는 중요하다. 그래서 꼭 Radial distortion을 calibration 하는 것이 중요하다.

Camera Pose

What if we move the camera?

이전까지는 카메라가 원점에 있다고 가정하고 수식을 유도했다. 이 경우, projection 수식은 단순히 3차원 세계 좌표를 2차원 이미지 좌표로 변환하는 데 초점을 맞추었다. ($(X, Y,Z)$ -> $(fX/Z, fY/Z)$)

그러나 항상 모든 카메라가 원점을 보고 있다고 가정할 수 없다. 그래서 알아야 할 것이 카메라가 움직였을 경우 그 변화가 어떻게 수학적으로 모델링 되는지이다.

카메라를 원점이 두기 전에, 또 다른 선형 변환이 하나 있다고 가정하면 모든 게 간단해진다. 즉, $X_{cam}$이 카메라가 세상의 중심인 3차원 좌표라면, 이 좌표계로 오기 위해 다른 어떤 회전(R) 이동(t) 변환이 있었다고 가정하는 것이다. 여기서 $X_{world}$란 이러한 변환이 있기 전의 3차원 좌표이다.

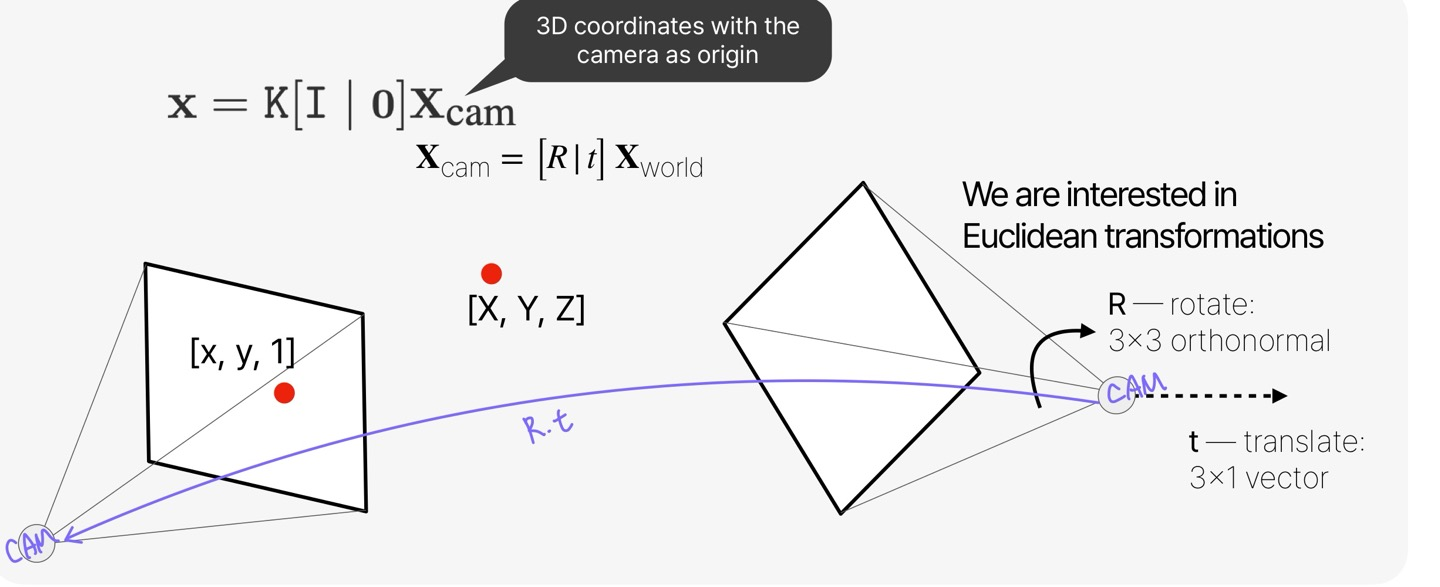
여기서 말하는 선형 변환은 SE(3) 변환 (2차원에서의 회전과 이동을 3차원으로 확장한 변환)을 의미한다. 다만 여기선 rotation을 위해 3x3 matrix를 사용하며, 이 matrix는 각 row 또는 column이 서로 orthonormal하다는 중요한 특징을 가진다.

Cam-to-world vs world-to-cam

world 좌표계에서 카메라가 원점인 좌표계로 변환하는 이 rotation을 world-to-cam 방식이라고 한다. 로봇이 어디에 위치해 있고, 주변 세상이 어떻게 구성돼 있는지를 다루는 SLAM 문제에서는 이 world-to-cam 방식을 많이 사용한다.

반대로 카메라가 원점인 좌표계에서 world 좌표계로 변환하는 방식을 cam-to-world이라고 한다. 주로 3차원 CAD 모델을 내 영상으로 옮겨 오고자 할 때 이 방식을 많이 사용한다.

두 좌표계 사이의 변환은 간단하다. 결론적으로 말하자면 w2c랑 c2w matrix는 서로 정확히 inverse 관계에 있고 translation 벡터들 같은 경우 형광펜 친 부분과 같은 관계가 있다.

Camera Calibration

다음 1999년도에 발표된 방법으로, 현실 세계에서 알고 있는 사물을 이용해 카메라의 K-Matrix 특성을 뽑아내는 알고리즘이다. calibration을 하기 위해 주로 사용되는 patten은 아래와 같은 checkerboard pattern이다.

이 알고리즘을 사용할 때 K와 여러 카메라 pose는 모르지만, 모든 이미지들이 같은 K를 활용하고, checkerboard corners의 3D 좌표를 알고 있다고 가정한다. 즉 월드 좌표계의 중심이 이 카메라 calibration pattern의 정가운데라고 가정하고 이 중심을 기준으로 corners의 상대적인 3D 좌표를 계산하는 것이다. 더불어 checkerboard는 2D 평면 위에 고정돼 있으므로 모든 점의 $z$ 좌표는 0으로 설정된다.

각 corner point는 앞에서 언급한 3D 좌표를 2D 좌표로 변환하는 수식을 통해 다음과 같이 나타낼 수 있다. 이 과정에서, 선형 변환이 homogeneous 좌표계에서 정의되기 때문에 lambda를 추가하였다. 어떤 값의 lambda를 곱하든 등식이 성립해야 된다는 걸 의미한다.

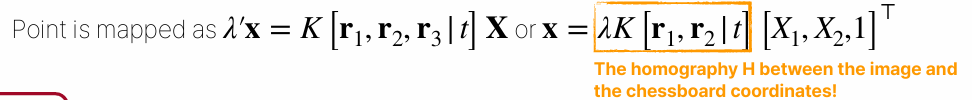
z=0을 가정했기 때문에 chessboard corners의 3D 좌표는 3차원이라고 하지만, 사실상 3차원에 존재하는 2차원 평면 위의 좌표이다.

이 점을 유념하고 다시 식을 보면, 이전에 배웠던 3차원을 거치지 않은 2차원간 변환이 떠오를 것이다. 즉, 가운데 노란색 박스로 표시한 부분이 homography나 다름이 없으니 homography 변환을 여기다 적용할 수 있다는 뜻이다.

그렇지만 아직까지 식을 다 푼 것은 아니다. 이미지마다 다른 $[r_1, r_2 | t]$가 문제가 되는 것이다. 따라서 앞서 언급한 rotation matrix의 중요한 특징을 사용한다.

다만, 이전처럼 $Ah = 0$ 이렇게까지는 정리할 수 없어서 다른 최적화 기반 방법(주로 사용되는 건 Levenberg Marquardt)들을 적용해야 한다.

---

여태까지 pinhole 카메라 model을 통해 이미지들을 연관시키고 중요한 calibration 방법을 살펴보았다.